低渗透油层弱水湿岩心的合理驱替速度

陈涛平， 张晓娇， 刘 斌

( 1. 东北石油大学 提高油气采收率教育部重点实验室，黑龙江 大庆 163318； 2. 大庆钻探工程公司 地质录井一公司，黑龙江 大庆 163114 )

0 引言

油藏岩石润湿性在很大程度上对孔隙中流体分布起着控制作用.水驱油时，地层原油采收率在很大程度上与水对地层岩石的润湿性有关[1-3]，而原油-岩石-盐水体系润湿性是一个复杂问题，不仅与原油组分、岩矿组分、地层水性质等密切相关，而且与流体接触时间的长短密切相关[4-8].毛管压力是低渗透岩心润湿性影响驱油效率的主要因素之一，岩石孔喉半径越小产生的毛管压力越大.一般认为，当油藏岩石为强水湿时，由于毛管压力是水驱油的动力，有利于提高水的自吸速率，因而与强油湿的岩石相比，其注水时的驱油效率应明显高些[9].油藏岩石的润湿性并不只限于强水湿和强油湿2种状态，而是覆盖着润湿指数从-1至1的一个广泛范围.Morrow N R[10]研究表明，当润湿性处于弱水湿或中性润湿状态时，驱油效率为最高.Anderson W G[9]将这些不同的结论归因于岩石非均质性、注水速率、孔隙几何形状，以及岩样的端面效应等其他因素的影响.姚凤英等[11]认为将亲油油藏润湿性转变为亲水或中性润湿，有利于提高采收率.文献[12]指出，润湿性影响水驱效果，且中间润湿的水驱采收率最高.宋付权等[13]研究润湿界面的滞后现象，指出液体在微管中流动的界面随着流速的不同其形状发生改变，在表面张力的作用下，微管的尺寸越小，2种流体的性质差别越大，界面的润湿滞后现象越不明显.在水驱油的过程中，动润湿滞后现象对采收率的影响很大，对于不同的渗透率、驱替速度以及润湿性，存在不同的采收率.当渗透率和润湿性一定时，必然存在一个最佳的驱替速度使得采收率达到最高.为此，笔者用人造岩心进行实验，探索低渗透油层弱水湿岩心的合理驱替速度.

1 动润湿滞后影响

润湿性是储层的一个基本特征参数，是控制油水在孔隙中分布状态和水驱油效率的一个重要因素，润湿滞后(尤其是动润湿滞后)是低渗透油层水驱油过程中必须考虑的一个重要因素，驱替速度影响动润湿滞后，所以驱替速度对水驱采收率的影响不可忽略.

1.1 采收率

在水驱油过程中，当三相周界沿固体表面移动时，因移动的延缓而使润湿角发生变化的现象即动润湿滞后.毛管数愈大，水驱残余油饱和度愈低.由Moore和Slobod[14]修正的毛管数可知：在不降低油水界面张力的情况下，当润湿角θ接近90°时，毛管数最大，此时水驱残余油饱和度最低，即中间润湿(θ=90°)水驱油效率最高.

在水驱油过程中，受到动润湿滞后的影响，接触角增大(见图1)，只有θ<90°的弱水湿岩样才能使动润湿角θ趋近于90°(图1(a)虚线)；θ=90°的中间润湿和θ>90°的弱油湿岩样都会使润湿角远离90°(图1(b)，(c)虚线)，润湿角的变化Δθ，即动润湿滞后影响的结果，使得θ+Δθ=90°时水驱采收率最高.

图1 动润湿滞后影响示意

1.2 毛管孔道驱替速度

岩石孔隙结构复杂，为了便于研究，将其假想成由等直径的平行毛管束所组成，流体在其中作定常层流流动.取其中一根长度为L，内壁半径为r的毛细管，水驱油过程中油水分布见图2(p1和p2为毛细管两端压力，θ1和θ2分别为水驱油动润湿滞后前进角和后退角).

图2 油段在等直径圆管中的定常层流流动

流体在等直径圆管中作定常流动时加速度值为0，无惯性力.考虑压力、摩擦阻力及毛管力，可得压力平衡方程为

p1-p2-pf+pc=0,

(1)

Δp=pf-pc,

(2)

式(1～2)中：Δp为毛管两端压差；pf为压力损失；pc为毛管力.

考虑毛管孔道中油水两相流，利用达西公式得

(3)

式中：Q为驱替排量；A为岩心截面积；μo和μw分别为油和水的黏度；Lo和Lw分别为油段和水段的长度；Ko和Kw分别为油相和水相的渗透率.

毛管孔道中油水两相流动的沿程压力损失为

(4)

式中：v为毛管中流体的流速；d为毛管直径；C为修正因数；ρo和ρw分别为油相和水相的密度；Reo和Rew分别为油相和水相的雷诺数.

考虑实际毛管孔道中有n个油段，则毛管力为

(5)

式中：σ为油水界面张力.

将式(3～5)代入式(2)，整理得

(6)

考虑到岩心迂曲度τ对毛管中流体速度的影响，有

v=τvD,

(7)

又根据孔道半径r、渗透率K及孔隙度φ之间的理论关系式

(8)

将式(7～8)代入式(6)，则有

(9)

由图2可以看出，θ1与θ2相关.由式(9)可以看出，接触角θ1，θ2，渗透率K，驱替速度vD之间相互影响且满足一定的关系式.又因润湿性对水驱采收率有影响[15]，所以θ1，θ2，K，vD之间必然存在合适的匹配关系，能使得水驱采收率达到最高.为此，有必要进行实验研究，以确定不同润湿性对应最高采收率时的(最佳)驱替速度，从而为分析驱替速度、渗透率、接触角三者之间的关系奠定基础.

2 实验

2.1 方案及设备

(1)方案.选用改变润湿性物质有十二烷基磺酸钠和硅油，分别用来制备亲水和亲油岩心.利用不同质量分数的处理液对岩心进行抽空饱和，经老化相同时间且烘干，制备出润湿性不同、其余性质相近的实验用岩心；然后用OCA-20视频光学接触角测定仪测量岩心接触角，测量5次取平均值，再进行饱和水，饱和油；最后进行水驱(水驱至含水率98%).

(2)设备.OCA-20视频光学接触角测定仪、SG83-1型双联自控恒温箱、JJ-1型电动搅拌器、Sartorius BS224S型电子分析天平、2XZ-8型真空泵等.

2.2 数据

实验所用岩心为低渗透圆柱状人造岩心，其实验数据见表1.

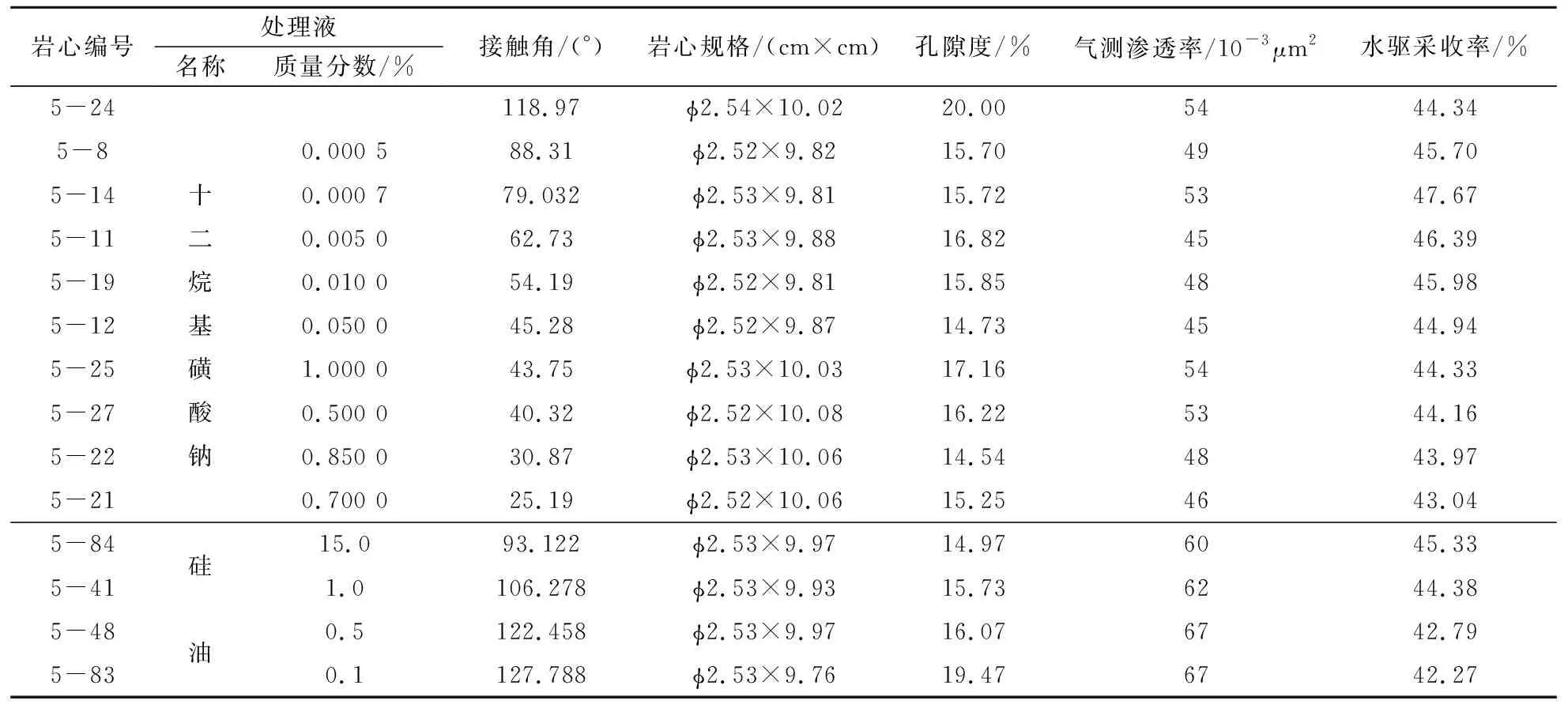
表1 人造圆柱状岩心及其实验数据

2.3 结果分析

2.3.1 水驱采收率与接触角的关系

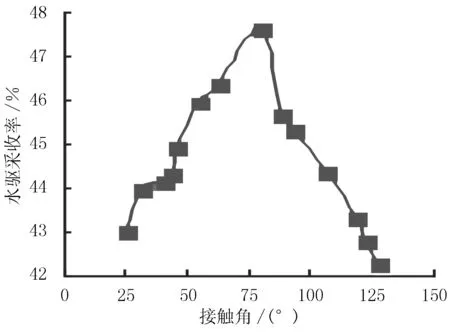
图3 水驱采收率与接触角的关系曲线

根据表1绘出水驱采收率随润湿接触角的变化曲线(见图3).由图3可以看出，当人造岩心接触角为79.032°时，水驱采收率最高为47.67%，即Δθ1=10.968°时其水驱采收率最高.因此，可将Moore和Slobod考虑润湿性给出毛管数Nc定义式修正为

(10)

2.3.2 合理驱替速度与渗透率的关系

根据实验结果，人造岩心接触角为79.032°时水驱采收率最高，此时由于动润湿滞后的影响使得θ1=90°，即油水界面垂直于管壁.

由于单个油段的长度有限，单个油段静止和流动2种状态的平均压力差有限，则可忽略水驱油过程中由压力变化所引起的单个油段的体积变化，按照体积守恒原理，单个油段在静止和流动2种状态下体积不变，即单个油段因水驱油前进角由θ变为θ1所减少的体积，等于其后退角由θ变为θ2所增加的体积.由θ1=90°、θ=79.032°及毛管半径r，可求得θ2=68.44°.

利用水驱油初始阶段的有关实验数据求得式(9)中的a和b，结合前面所求的θ1和θ2，采用试算法求得C≈1，n=9.24.

在实验条件下，则式(9)可以写成

(11)

式中：k为比例系数，且k=72.3 s-1.

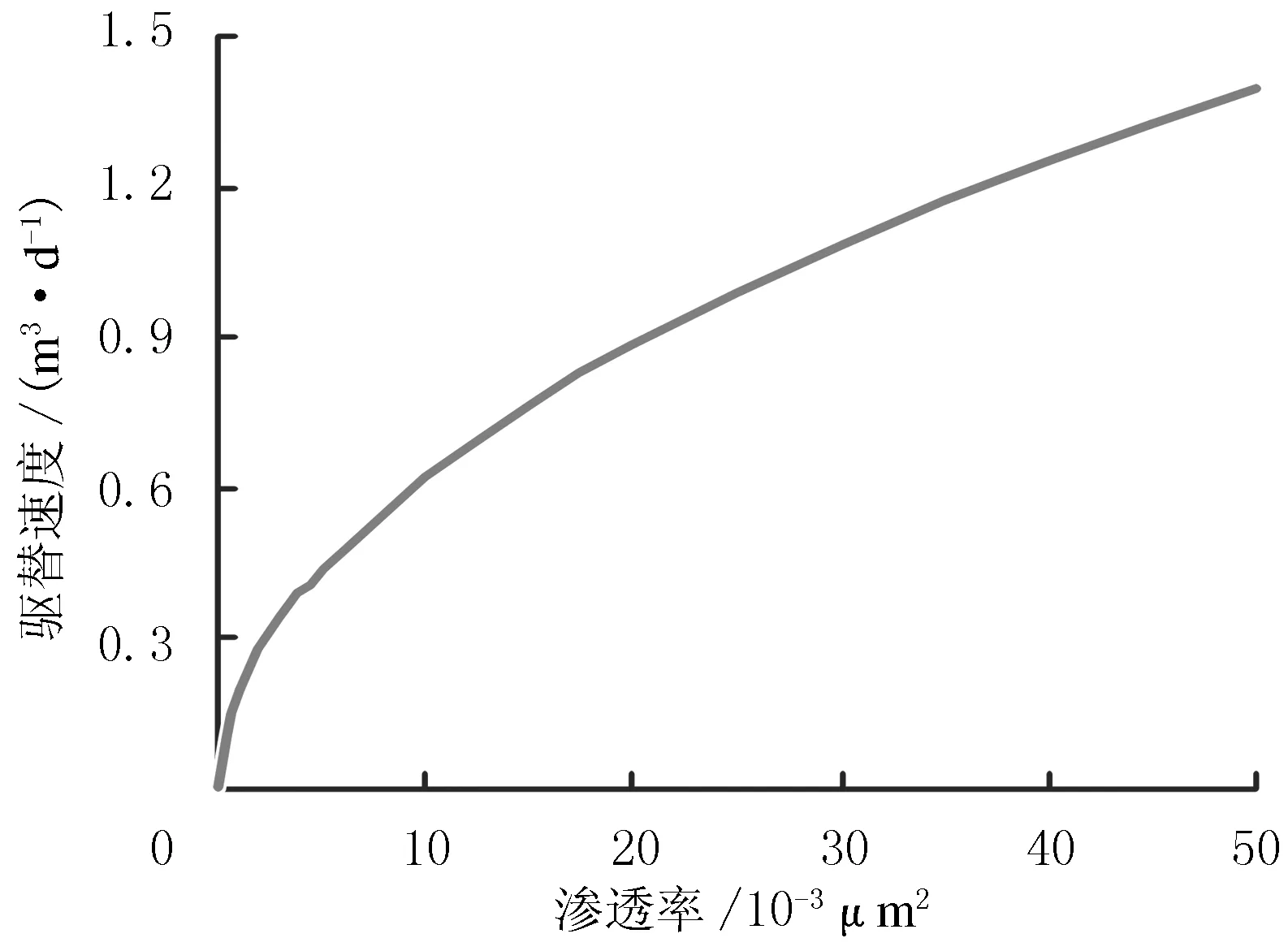
图4 驱替速度与渗透率的关系曲线

根据式(11)作驱替速度与渗透率的关系曲线(见图4).对于低渗透油层，欲使水驱采收率达到最高，则驱替速度与渗透率应满足图4的二次曲线关系.

由图4可以看出：当水驱采收率最高时，驱替速度随着渗透率的增大而增大，但渗透率增大的幅度比驱替速度增大的快，即当渗透率很大时，驱替速度也不会太高.因此，一定渗透率的岩心必然存在一个最佳驱替速度，使得水驱采收率达到最高.不同渗透率的岩心有不同的最佳驱替速度，对应一个合理的驱替压力梯度，从而能获得最高的水驱采收率.当岩心渗透率为50×10-3μm2时，合理驱替速度为1.4 m/d.

3 结论

(1)若将岩石孔隙假想为等直径平行毛管束，考虑动润湿滞后影响，低渗透油层弱水湿岩心的合理驱替速度与渗透率之间符合二次曲线关系；当岩心渗透率为50×10-3μm2时，合理驱替速度为1.4 m/d.

(2)人造岩心接触角为79.032°时，其水驱采收率最高为47.67%，可以认为动润湿滞后的前进角变化为10.986°.

(3)考虑动润湿滞后影响，在Moore和Slobod毛管数定义式的基础上，应对毛管数公式进行适当修正.