基于分布式粒子群算法的翼型优化设计

李 静，高正红，黄江涛，赵 轲

(西北工业大学翼型叶栅空气动力国防科技重点实验室，陕西西安 710072)

0 前言

随着计算机技术和CFD技术的高速发展，用数值方法结合CFD求解器进行气动优化设计越来越受到人们的重视，而稳定性、全局性和高效性又是优秀的优化设计方法必须具备的。自1995年Eberhart和Kennedy提出标准粒子群算法以来，它便以其高效的搜索效率以及简捷的程序模式等优点，在神经网络训练、参数辨识以及任务调度等领域得到了一定的应用［1－3］。然而标准粒子群算法本质上是一种随机算法，即使采用相同参数还有可能陷入局部最优点，而且大量的CFD计算降低了这一设计方法的设计效率，增长了设计周期。

本文一方面将自然选择机理与粒子群优化算法相结合，形成一种基于自然选择的粒子群优化算法(SELPSO)，以改善群体的多样性及算法的全局收敛性和求解精度。另一方面，本文将分布式计算引入到改进的粒子群算法中，形成了基于分布式粒子群算法的优化设计系统，提高了粒子群算法的优化设计效率，缩短了设计周期。将上述系统用于跨音速翼型减阻设计，取得了显著的效果。

1 基于自然选择的粒子群算法及性能测试

标准粒子群优化算法是模拟鸟群飞行觅食行为，在每个粒子发现的最优解和整个粒子群发现的最优解的引导下迭代搜索到全局最优解。首先随机初始化粒子种群位置和初速度，然后计算出每个粒子的适应值，每个粒子记住自身所找的个体最优粒子pbest以及迄今为止找到的全局最优粒子gbest，用粒子当前速度、pbest和gbest的位置来更新粒子速度，从而在下一个时刻粒子能飞行到新的位置进行搜寻。

在标准粒子群算法中，粒子逐一搜索它的邻居以确定最优解粒子，从而用最优解粒子的信息校正自己的搜索路线。它建立在下面的假设上［4－5］:在t时刻找出的最优邻居，比其他所有邻居都处于一个更好的搜索区域，这个区域包含或者更靠近真正的全局最优解。然而这个假设未必成立，因为某时刻最优邻居未必靠近全局最优解，有可能处于一个局部极值的周围，只是其适应值暂时处于最小，从而被认定为最优粒子，而真正靠近全局最优解的也许是适应值排在第二乃至更后面的粒子。因此仅凭单个“最优邻居”的引导，而忽略其他邻居，则信息来源单一，搜索区域的真实信息就有可能被遗漏。随着迭代次数的增加，粒子群算法搜索最优解的能力将会大大降低。

基于自然选择的粒子群优化算法是在每次迭代过程中将整个粒子群按适应值排序，用群体中最好的一半粒子的速度和位置替换最差一半的速度和位置，提高最优粒子周围其他邻居的信息利用率，同时保留原来每个个体所记忆的历史最优值。提高对搜索区域的信息利用率，进而改善群体的多样性及算法的全局收敛性和求解精度。

(1)算法步骤

基于自然选择的粒子群算法的基本步骤如下:

①随机初始化种群中各微粒的位置和速度;

②评价每个微粒的适应度，将当前各微粒的位置和适应值存储在各微粒的pbest中，将所有pbest中适应值最优个体的位置和适应值存储于gbest中;

③更新每个微粒的速度和位置;

④对每个微粒，将其适应值与其经历过的最好位置作比较，如果较好，则将其作为当前的最好位置;

⑤ 比较当前所有pbest和gbest的 值，更新gbest;

⑥将整个粒子群按适应值排序，用群体中最好的一半粒子的速度和位置替换最差的一半速度和位置，保持pbest和gbest不变;

⑦若满足停止条件(通常为预设的运算精度或迭代次数)，搜索停止，输出结果，否则返回(③)继续搜索。

速度更新以及位置更新方程为:

其中，ω为惯性权因子，r1和r2为0到1之间均匀分布的随机数，c1和c2分别为自我总结因子和向最优个体学习因子。

在文中的翼型优化算例中，随机初始化30个翼型，设计变量表达了其位置，速度为(0，1)之间的随机数，每个翼型的阻力系数Cd加上罚值表达每个微粒的适应度。

(2)算法性能测试

选取Rastrigrin函数作为测试函数，该函数在定义域内有多个极小值，最小值处于(0，0)点，该测试函数表达式为:

其中，取 n=2，xi∈(－2，2)

图1显示了该测试函数的空间曲面分布，可以看到该函数是一个多峰值的函数，在优化过程中很容易陷入局部最优，而无法搜寻到全局的最优解。图2为标准粒子群算法(PSO)的一次失败的搜索结果，在此次搜索中，算法过早地收敛到局部最优值。

图3为标准粒子群算法(PSO)及基于自然选择粒子群算法(SELPSO)的性能比较，可看出基于自然选择粒子群算法比标准粒子群算法提高了全局最优搜索能力以及收敛速度。同时，在第100代时，基于自然选择粒子群算法寻得的最优解为:x1=0.000003，x2=0.000004精度达到10－6，而标准粒子群算法寻得的最优解为:x1=0.000020，x2= －0.000020，精度只有 10－5。

2 分布式计算及效率测试

相对于其他的一些优化设计方法，采用粒子群算法的优化设计，由于每代都要计算几十个个体的适应值，这对于CFD分析来说计算量特别大，尤其是对于复杂外形的气动问题。因此，有必要减少每代的CFD计算时间，提高优化速度来缩短周期。而粒子群算法的基本结构及特征又决定它适合采用分布式计算来提高优化速度。

本文是基于分布式计算引擎来实现分布式粒子群优化算法。分布式计算引擎提供的功能可以将应用程序分割为能在多个 worker(即多个单独运行的计算引擎)上独立执行的任务。优化算法中，耗时最多的是CFD分析计算部分。对于粒子群算法，每代个体中所有粒子的CFD分析是相互独立的，因此可以分割成多个相互独立的任务在多个计算引擎上分别进行CFD分析计算。

(1)算法流程

分布式应用程序的工作流程一般是:

①寻找一个作业管理器job manager(或者作业调度程序(scheduler))——寻找一个作业管理器或者作业调度程序的函数FindResourcejob在当前内核中创建一个对象，用来表示将要运行作业的作业管理器或者作业调度程序。

②创建一个作业job——创建作业用以产生一个任务集合。作业存在于作业管理器中，而一个在本地内核中的作业对象代表相应的作业。

③创建任务tasks——创建任务添加到作业中去，可以用本地内核中的任务对象表示作业中的每一个任务。

④提交作业job到待执行的任务队列——当作业的每一个任务都被定义之后，将它提交到作业管理器或者作业调度程序。它们将任务分配到各个节点执行，当各节点的所有任务执行完毕后，作业将被标记为完成状态。

⑤返还作业结果。

⑥销毁作业——当所有作业完成，结果收集回来后，需要销毁作业以释放内存。

由于采用了多线程的分布式计算模式，提高计算资源利用率的同时，提高了计算效率。

(2)效率测试

由于分布式计算过程中，创建作业和任务，提交作业以及返还结果等都要耗费一定的时间，因此简单的函数计算或者其他不耗机时的计算是不能体现分布式的效率的。为验证分布式计算的效率，选取了一个比较复杂，计算量大的函数作为测试函数:

其中，x为30行×19列的矩阵，n=5×106。

计算每一个y值需要58.4s，如果采用串行算法，计算30个y则需要1751.6s。表1为采用串行计算和分布式计算所耗费计算机时的比较。图4为采用分布式算法计算时间及计算速度的比较。

当用一个Worker进行计算时，所耗费的时间为1762.64s，与串行算法相比多用了11s，这一部分时间用来创建作业和任务，提交作业以及返还结果等。从表1中可以明确看出，随着Worker的增加，分布式计算所耗费的计算机时迅速的减少。

从图4也可以看出，随着Woker的增加，进行计算所耗费的时间迅速的减少，而计算速度在一定范围内呈现了线性增长的趋势。因此，采用分布式计算对提高运算效率有很大帮助。

表1 不同计算方法耗费机时比较Table 1 The comparison of computing time between serial computing and distributed computing

图4 分布式计算Fig.4 The distributed computing

3 CFD分析方法及翼型参数化

文中通过求解双曲线方程生成结构网格，以保证网格在物面处的正交性。

基于结构网格离散求解雷诺平均Navier-Stokes方程进行CFD数值模拟，采用AUSMDV空间离散方法，SA一方程湍流模型，LU-SGS隐式时间推进方法，多重网格加速收敛。

以 Ma=0.75，α =2.72°，Re=6.2 × 106状态时的RAE2822翼型来检验气动分析的准确性。计算网格为2.56万，图5给出了翼型压力分布的计算结果与实验数据的对比。从图中可以看出，计算结果与实验结果基本吻合，可见本文中的气动分析是相对准确的。

本文的设计中，翼型的几何形状通过解析函数线性叠加来表示，采用经典Hicks-Henne函数。Hicks-Henne函数对翼型上下表面各关键点形状的影响平滑均衡，既可保证对翼型关键点形状的调整，又可保证关键点与翼型整体形状的平滑。取型函数的系数作为设计变量，与基准翼型和固定的前后缘点来确定翼型形状:

图5 RAE2822翼型压力分布计算结果与实验结果对比Fig.5 The airfoil pressure distribution of RAE2822 Compared with Experiment and CFD

4 算例分析

以RAE2822翼型为初始翼型进行减阻优化设计，设计状态为:

优化目标为最小化翼型阻力，翼型阻力加上罚值即优化算法中微粒的适应度。约束条件为最大厚度不减小，若厚度不满足约束，即对目标函数值进行惩罚。CFD分析计算中保持升力系数不变。该优化问题的数学模型可描述为:

在优化算法中，每代采用30个粒子，最大迭代次数为60次。在单机四核的处理器上完成分布式计算，四个进程分别处理不同的粒子，当某个线程空闲时，立即向该线程发送新的任务。

每个粒子的计算网格均为2.56万，在进行CFD分析时每个粒子要耗费1.72分钟，每代CFD分析耗费的时间大约为51.6分钟。采用分布式计算，每代个体只需要16分钟就可以完成CFD分析计算，在很大程度提高了计算效率，缩短了优化周期。

表2为优化前后翼型性能比较，图6－7分别给出了采用分布式SELPSO优化前后翼型的形状以及相应的翼型表面压力分布，图8和图9分别给出了优化前后翼型的等马赫数云图。从表二中可以看出，在保持升力系数不变及翼型最大厚度不减小的情况，原始翼型的阻力系数为0.01307，优化后翼型的阻力系数为0.01093，优化前后阻力系数降低了21.9 counts。从翼型表面压力分布上可以看出，优化后的翼型已经消除了强激波。从图8和图9的对比中可以看出，优化前的翼型在上表面存在一道很强的激波，而优化后的翼型已基本上消除了强激波。

表2 优化前后翼型性能比较Table 2 The comparison of airfoil performance between initial and optimized airfoil

5 结论

本文构建了基于自然选择的粒子群优化算法的气动优化设计系统，通过典型算例测试，结果表明，该改进型粒子群算法克服了标准粒子群算法收敛慢，容易陷入局部最优等缺陷。它具有很好的全局搜索能力，并提高了算法的收敛速度。

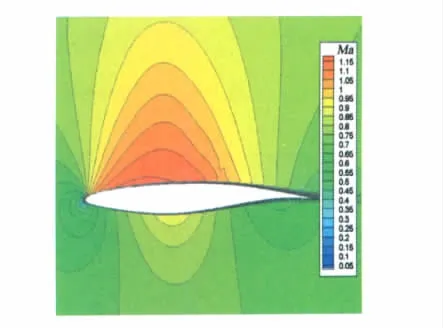
图9 优化后翼型等马赫数云图Fig.9 The Mach number contour of optimized airfoil

为提高优化系统的设计效率，本文将分布式计算引入到改进的粒子群算法中，解决了优化算法中CFD分析耗机时的缺陷，提高了设计效率，缩短了周期。将该系统用于跨音速翼型减阻设计，很大程度上改善了翼型的气动特性，并提高了设计效率。

文中算例是在单机四核的处理器上完成分布式计算，计算效率提高了3倍多。若将分布式计算应用于高性能的计算机群，相信对计算效率还会有更大的改善，这就为复杂外形的气动优化设计提供了一个很好的平台。

［1］KENNEDY J.The particle swarm:social adaptation of knowledge［A］.IEEE international Conference on Evolutionary Computation［C］.IEEE Service Center，1997，303－308.

［2］BOERING D W and WERNER D H.Particle swarm optimization versus genetic algorithms for phased array synthesis［A］.IEEE Transactions on Anetnas and Propagation［C］.2004，52(3):771－779.

［3］高尚，韩斌，昊小俊等.求解旅行商问题的混合粒子群优化算法［J］.控制与决策，2004，19(11):1286 －1289.

［4］王凌.智能优化算法及应用［M］.北京:清华大学出版社，2004，18 －21.

［5］KENNEDY J，EBERHART R C.Particle swarm optimization［A］.Proc.IEEE International Conference on Neural Networks［C］.1995，Vol.4:1942 －1948.

［6］王晓鹏.遗传算法及其在气动优化设计中的应用研究［D］.［博士学位论文］.西北工业大学，2000.

［7］詹浩，白俊强，华俊.基于分布式遗传算法的多段翼型优化设计［J］.西北工业大学学报，2004，22(1):92－95.

［8］熊俊涛，乔志德，韩忠华.基于Navier-Stoke方程跨声速翼型和机翼气动优化设计［J］.空气动力学学报，2007，25(1):30 －33，44.

［9］程文渊，常艳等.基于分布式计算的复合材料机翼优化设计［J］.复合材料学报，2007，24(1):167－171.

［10］龚纯，王正林.精通MATLAB最优化计算［M］.北京:电子工业出版社，2009.

［11］许平，姜长生.基于粒子群算法的翼型优化设计［J］.飞机设计，2008，28(5):6 －9.

［12］RAJAN S D and BELEGUNDU A D.Finite element analysis＆design optimization in a distributed computing environment［R］.AIAA－2004－4453.