利用留数计算广义积分

区燕玲 陈麒羽 陈丽娟

（华南师范大学数学科学学院 广东广州 510631）

利用留数计算广义积分

区燕玲 陈麒羽 陈丽娟

（华南师范大学数学科学学院 广东广州 510631）

利用留数来计算实函数的广义积分可以带来很大的方便。本文总结了几种可以利用留数来计算的广义积分的类型，对某些类型进行了推广，并且在原有文献的基础上弱化了某些条件。

留数；留数定理；广义积分；有理函数；三角函数；对数函数；幂函数

定理1[1]：设是有理函数，分母在实轴上不为零，并且分母的次数要比分子的次数至少高2。那么其中表示函数f(z)在上半平面内的所有孤立奇点处的留数总和。这就是我们常说的“围道法”，我们就不作证明了。

Jordan引理[2]：设函数f(z)在半圆周R充分大)上连续，且在圆弧CR上一致成立，则

定理2[2]：设为有理函数，如果P(x)，Q(x)满足下列条件：

(1)Q(x)比P(x)的次数至少高一次；

(2)在实轴上，()0 Q x≠；

图1

证明：令（如图1所示），其中CR+L为正取向(逆时针方向)，则：令：R→+∞，有：

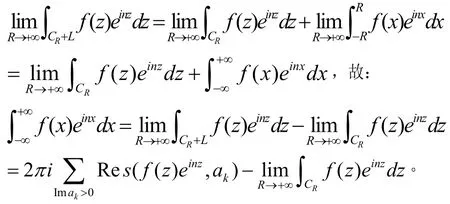
又因为Q(x)比P(x)的次数至少高一次，故在CR上，由Jordan引理，得故故定理可证。

推论1：设为有理函数，如果P(x)，Q(x)满足下列条件：

(1)Q(x)比P(x)的次数至少高一次；(2)在实轴上，Q(x)≠0；(3)m, n>0。则：

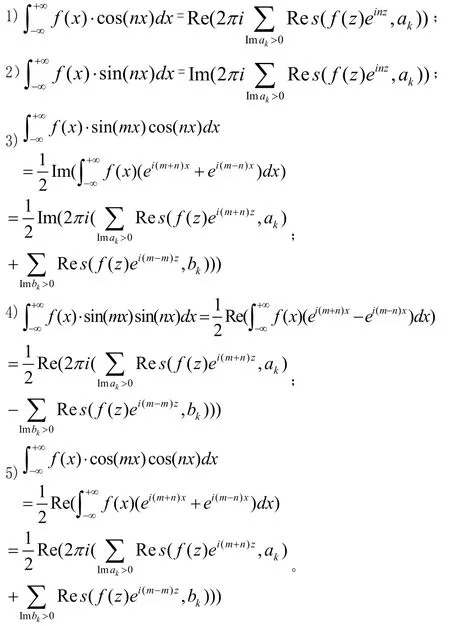
证明：由于1)、2)显然可证。再由积化和差公式以及1)、2)结论，3)、4)、5)均可证。

引理1[1]：设函数f(z)在上连续，而且其中A有限，则其中ΓR为位于D内的圆弧方向去逆时针方向。|

引理2[1]：设函数f(z)在圆环形闭区域：上连续，记的方向为逆时针，若其中A有限，则

其实，定理2中的条件(2)还可弱化，将其推广得到如下定理:

定理3[2](定理2的推广)设为有理函数，如果P(x)，Q(x)满足下列条件：(1)Q(x)比P(x)的次数至少高一次；(2)在实轴上，Q(z)至多只有一阶零点；(3)m>0。则其中表示函数在上半平面内的所有孤立奇点处的留数总和，而表示函数在实轴上的所有一阶极点处的留数总和。

证明：若在实轴上，Q(z)≠0，由定理2和可证定理成立。否则，不失一般性，不妨设Q(z)在实轴上仅有一个一阶零点z0，由反常积分柯西主值的定义如图2，取上半圆周以及上半其参数方程为圆周其参数方程为使得在上半平面内的所有孤立奇点全含于CR及Cr与实轴上的直线段及所围成的有界区域内。由题设在该区域加边界所构成的有界闭域上解析，由留数定理即又因为Q(x)比P(x)的次数至少高一次，由Jordan引理，又z0为的一阶极点，由引理2有故

图2

定理4[2]：若实有理函数满足：P(x) Q(x)互质，Q(x),在上恒不为零。且分母的次数要比分子的次数至少高2次，则：

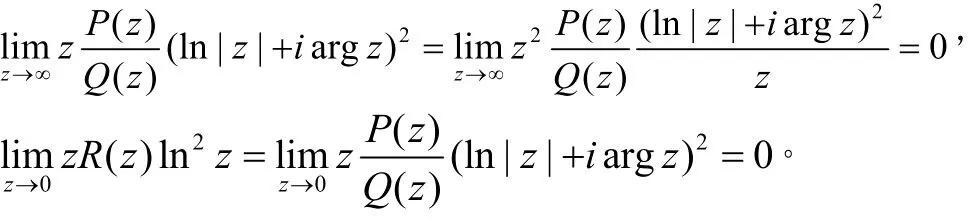
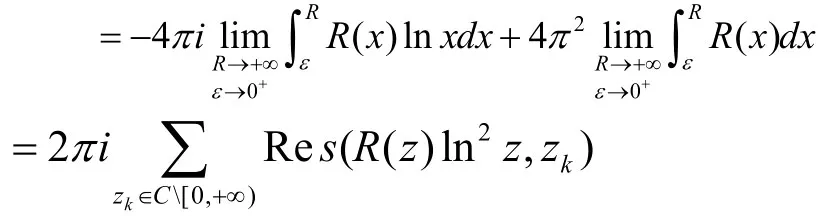
图3

定理4的推广[3]：设是只有有限个极点且在半实轴x≥0上无极点的亚纯函数，分母的次数至少比分子的次数高2次，有：

定理5[2]：若实有理函数满足：P(x)和Q(x)互质，Q(x)在上恒不为零，且则其中zα为上满足的解析分支（即主值支），zk为在内的孤立奇点，即Q(z)在C[0,+∞)内的零点。

证明：由反常积分柯西主值的含义作辅助函数并记Q(z)在内的零点为显然这样的零点至多只有有限个。

如图4，取充分大的正数R和充分小的正数ε，使Q(z)在C[0,+∞)内的零点都含于点集内。考虑函数沿D的边界的正向积分，由留数定理得，并注意到当时，得：

定理可证。

图4

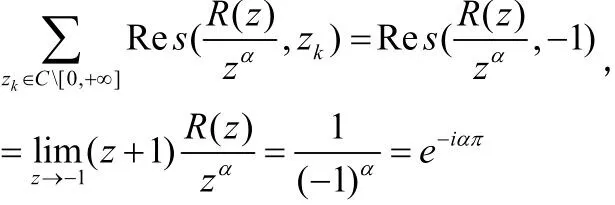
所以：

[1]陈宗煊，孙道椿，刘名生.复变函数[M].科学出版社，2010

[2]刘敏思，欧阳露莎.复变函数论[M].武汉大学出版社，2010.

[3]张毅.应用留数定理计算一类实积分[J].大学数学，2010.

区燕玲（1989-），女，广东云浮人，华南师范大学数学科学学院本科生研究方向：数学与应用数学。

2010-11-27