计算机辅助装调与传统基准传递技术相结合实现三镜消像散系统的装调

朱时雨，张 新，李 威

(中国科学院长春光学精密机械与物理研究所，吉林长春130022)

1 引言

近年来，随着航天遥感系统复杂程度的提高，对其精度要求也越来越高，而系统装调是实现理想系统精度的关键步骤。目前，对于全反射、无中心遮拦、大视场、全波段应用的光学系统，传统装调方法已无法满足其接近或超过衍射极限的要求，而计算机辅助装调与传统方法相结合使这类光学系统的成功装调成为可能。

80年代初期，国外开始从事离轴三镜系统计算机辅助装调的研究［1-2，4］。近几年，国内也开始了这方面的研究，并进行了计算机模拟与简单光学系统的计算机辅助装调方法实践，取得了一定的进展，其中失调量常采用阻尼最小二乘法来求得［3］。

三镜消象散系统(Three-mirror Anastigmat，TMA)是现阶段航天相机普遍采用的光学系统，推扫观测为其主要工作方式。与传统同轴光学系统相比，其优点是能够平衡系统对视场、对地分辨率、重量及波段等重要技术指标的要求，现已成为国际上普遍采用的光学系统。该光学系统由3片全反射式离轴非球面镜片组成，主、次及三镜光轴重合为系统光轴。由于系统本身的特点，其设计、加工及集成难度较高。

本文采用计算机辅助装调与传统基准传递相结合的方法对大视场TMA系统进行装调，综合利用两者的优点，装调后检测得到的光学系统精度满足设计要求，大大缩短了装调时间，较好地完成了整体项目任务，验证了两种技术相结合在复杂光学系统装调中的优势。

2 传统基准传递技术与计算机辅助装调技术

典型的TMA光学系统如图1所示。常用的装调方法主要有基准传递技术和计算机辅助装调技术。

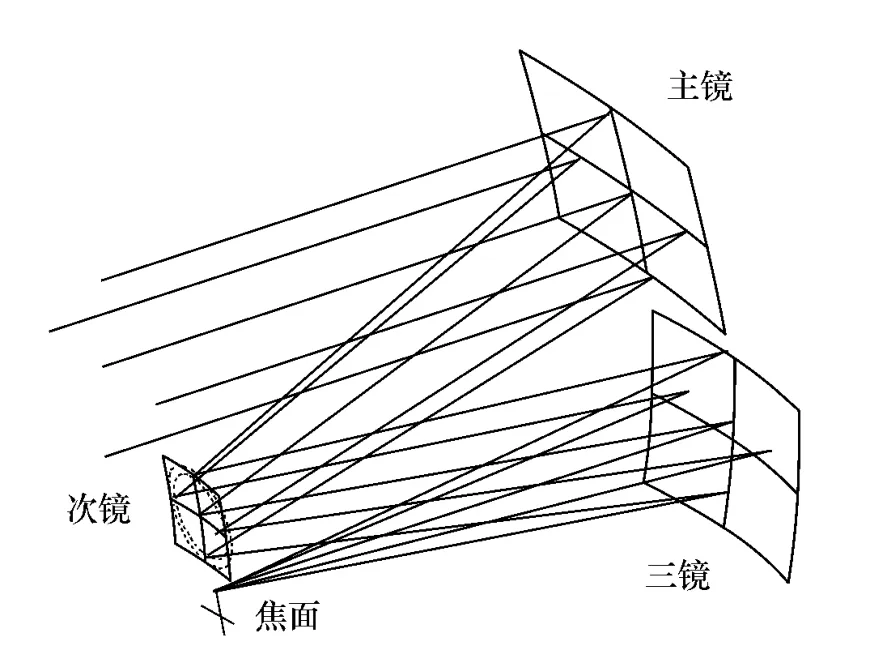
图1 TMA系统光学示意图Fig.1 Optical diagram of TMA system

2.1 传统基准传递技术

传统装调技术以其直观的表述形式，可以迅速传递公差分配，其可靠的基准得到普遍的认可。在卡式系统中，采用定心装调技术找出主次两镜光轴(光轴指向方向标定精度较高，位置标定精度较低)，在最终装调时实时监视，只需调整次镜三方向位移即可实现两镜最佳相对位置，而此三方向位移产生的像差是极为明显的，可进行人为判读。但对于精度较高的航天系统来说，由于光学形式及机械结构的限制，镜面数量增加，可选用基准相对减少，波前像差产生的原因十分复杂，无法根据像差进行人为判读装调。

2.2 计算机辅助装调技术

作为干涉测量技术与Zernike像差理论的延伸，计算机辅助装调技术有着较高的精度与成熟的软件算法支持［5-6］，已在单镜检测、两镜系统中得到验证。但对于三镜或四镜光学系统，由于自由度较多，初始调整后波相差较大，完全采用阻尼最小二乘法计算将不能获得最佳收敛结果。在此项目中，粗调后通过干涉仪收集5个视场波前像差，见表1。表中Z5至Z9为实际光学系统与理想光学系统的差异，分别代表0°方向像散、45°方向像散、0°方向彗差、90°方向彗差、球差。这些参数的大小决定了系统成像质量的优劣。

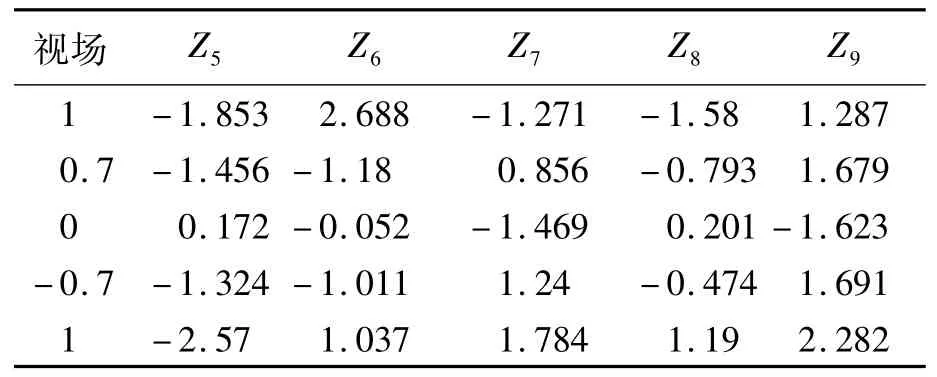
表1 TMA系统各视场Zernike系数Tab．1 Zernike cofficients of TMA system in different view of fields

将数据结合光学结构输入到CODEV软件中进行计算，得到的失调量见表2。

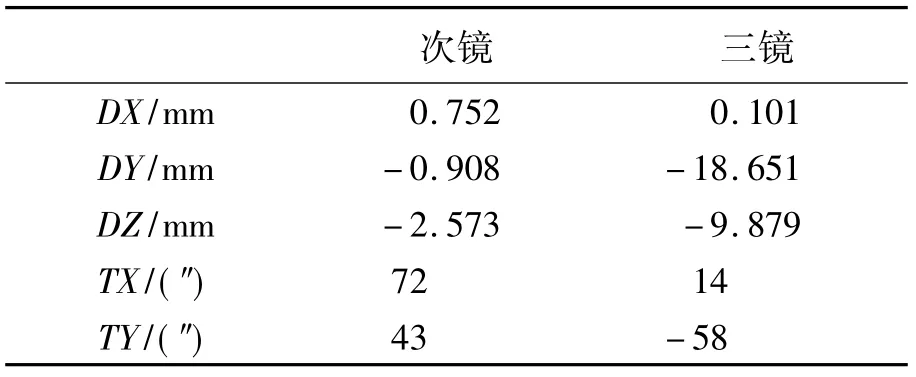
表2 失调计算(以主镜为基准)Tab．2 Values of misalignment(primary mirror as the datum)

其中三镜Y方向需要平移18 mm，这对于光学系统来说是明显错误的解，按照此失调量进行调整后像差明显增大，产生这种现象是由于失调量的近似算法引起的。

3 计算机辅助装调数学模型

采用阻尼最小二乘法进行光学设计与失调量的计算［7］，像差线性方程组矩阵形式为：

定义方程：

式中：φ为像差残量，A为灵敏度矩阵，△x为调整变量，△F为相差增量，即测定值与设计值之差。取各像差残量的平方和构成另一个函数Φ(△x)：

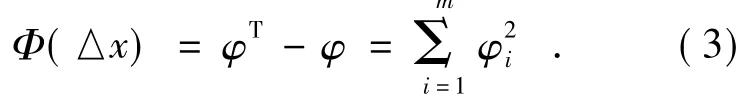
Φ(△x)的极小值解称为像差线性方程组的最小二乘解，目的是使像差残量最小：

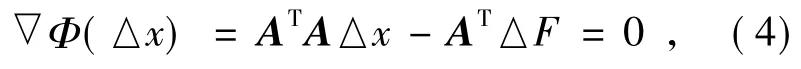
即

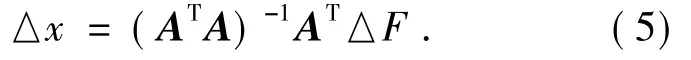
在比较复杂的光学系统中需进行优化计算的结构参数很多，在若干自变量之间会出现近似相关的现象，这就使矩阵(ATA)的行列值接近于零，(ATA)接近奇异，最小二乘法求出的解很大，超出了近似线性的区域，因此需对解向量的模进行限制，改为求下列函数的极小值解：

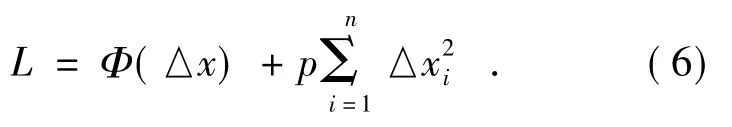
其目的是既要求评价函数Φ(△x)下降，又希望解向量的模△x2=△xT△x不要太大。

i

即

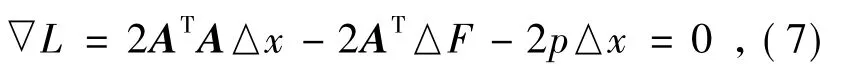
或

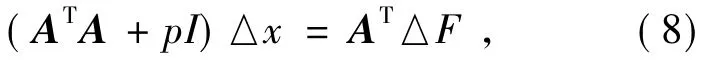
则：

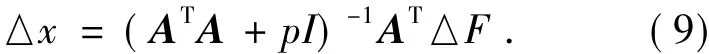
这样改进后即为阻尼最小二乘法，p为阻尼因子。

然而像差与结构参数之间的关系是非线性的，在阻尼最小二乘计算过程中，像差与结构参数之间越接近线性，才越有可能使Φ(△x)下降。而实际情况是：在装调初期，由于各参数偏离理论位置较大，即△F很大，导致F与A呈非线性，阻尼最小二乘的近似解与实际值相差较大，无法指导装调，因此，在实际复杂光学系统装调中，应遵循以下原则：

(1)通过减少失调变量从而减少各变量之间的近似相关性。

(2)提高初始调整后的精度，使像差与结构参数之间接近线性。

4 计算机辅助装调与传统基准传递技术的结合

在系统装调过程中，首先通过传统定心装调方法找出3片镜光轴并监视调整使之重合(光轴指向方向标定精度较高，远小于公差要求，可作为基准不动;位置标定精度较低作为变量优化)。这时，3片镜倾斜自由度已经确定(以主镜为基准)，失调变量减少为6个，同时偏心的位置误差也已很小，如图2所示。

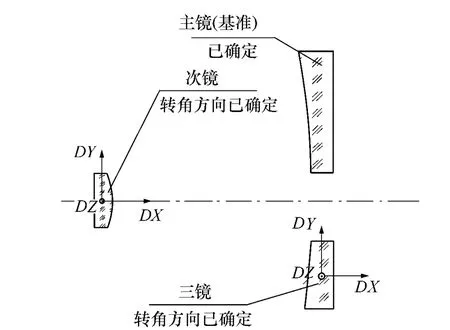
图2 调整示意图Fig.2 Sketch map of adjustment

此时采集光学系统的各视场Zernike系数见表3。

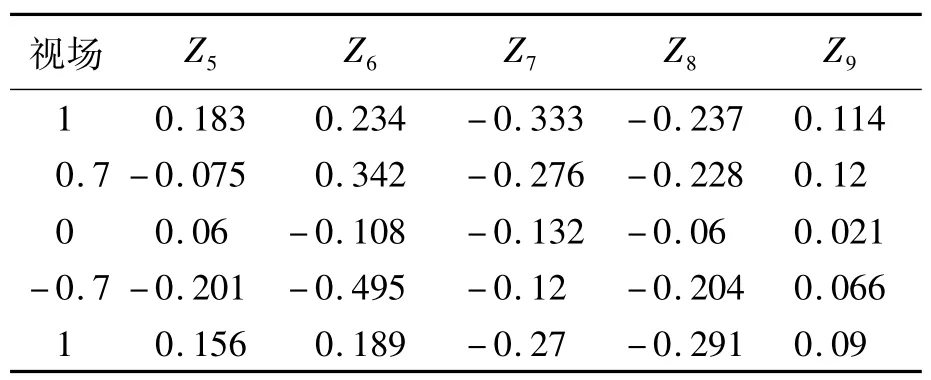
表3 TMA系统各视场Zernike系数Tab．3 Zernike cofficients of TMA system in different view of fields

将数据输入到CODEV软件中进行失调计算，得到的失调量见表4。

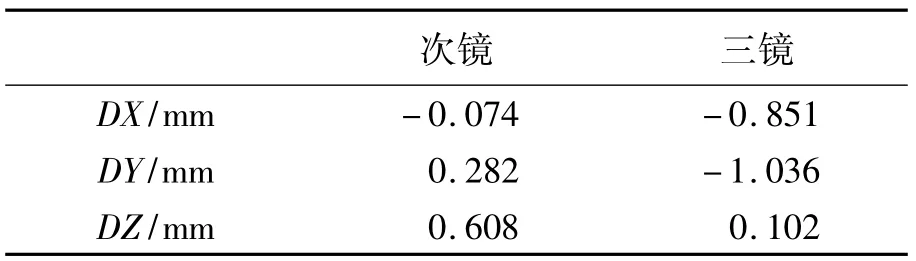
表4 失调计算(以主镜为基准)Tab．4 Values of misalignment(primary mirror as the datum)

系统经过一次调整后，得到的各视场Zernike系数已经很小，再次经过计算调整后各视场波前如图3所示，波前像差均已经达到1/14λ(RMS)。

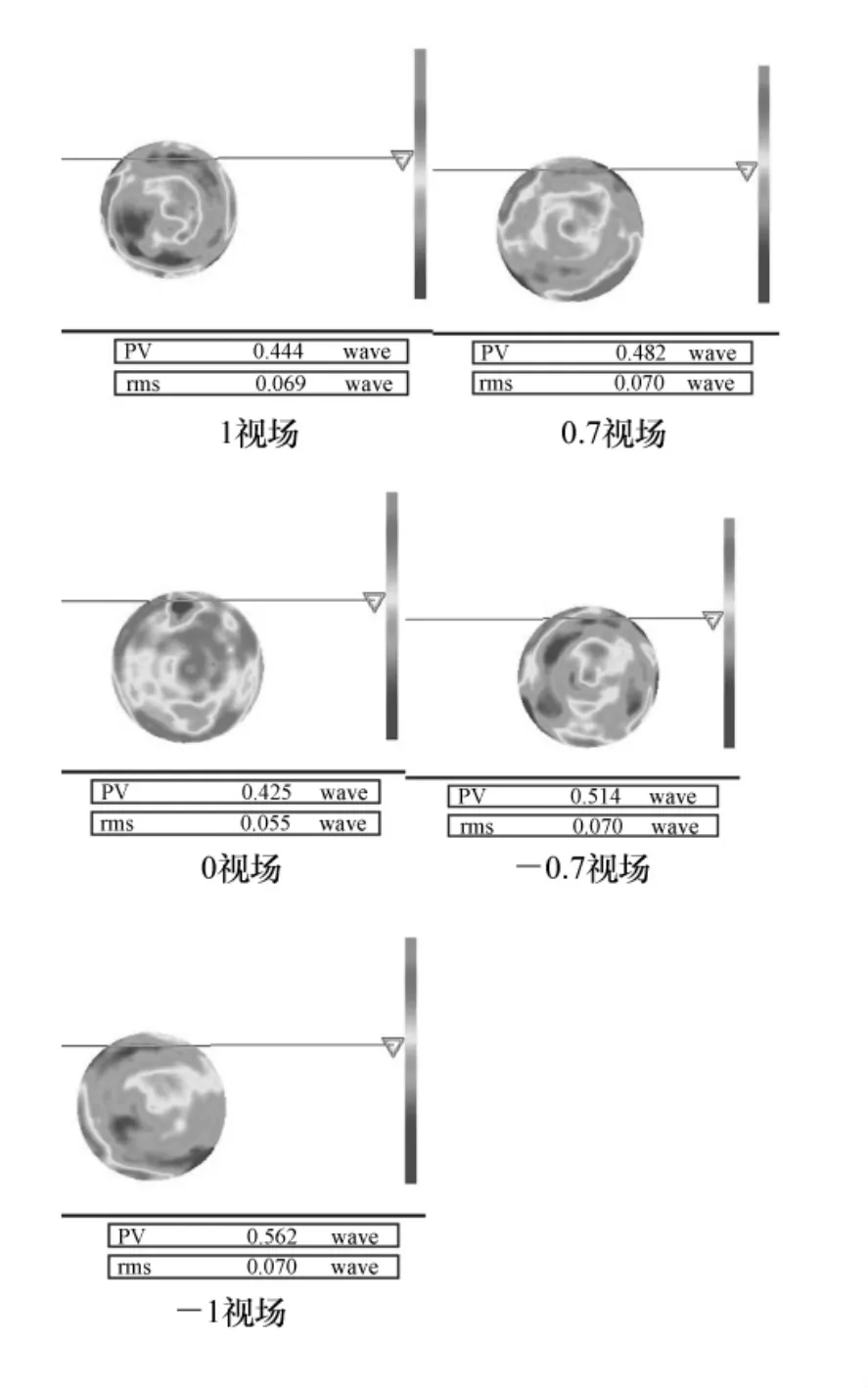
图3 各视场波前干涉图Fig.3 Wavefront interference patterns in different view of fields

5 结论

本文对先进的空间相机光学系统之一，TMA系统的装调进行了研究。在实际装调工作中，以传统定心方法为基础，以计算机辅助装调方法为指导，结合二者的优点，使其更有效地适用于复杂光学系统的装调。由于在装调过程中，温度变化、镜面本身受力变形、镜面实际参数的加工测量误差、理论计算坐标与实际坐标的偏差以及数据采集的准确性等干扰因素较多，干扰因素排除得越好，计算机辅助装调的指导性越强。通过两种方法的结合，使三镜在Y向和Z向的失调量由18.651和9.879 mm提高到1.036和0.102 mm，系统波前差也达到全视场平均值为1/14λ(RMS)，从而大大缩短了装调时间，提高了装调效率，对复杂光学系统装调提供了有价值的参考。

［1］ YANG H S，KIM E D，CHOI Y-W，et al..Alignment methods for cassegrain and RC telescope with field of view［J］.SPIE，2004，5528：334-341.

［2］ FIGOSKI J W，SHRODE T E，MOORE G F.Computer-aided alignment of a wide-field，three mirror，unobscured，highresolution sensor［J］.SPIE，1989，1049：166-177.

［3］ 张斌，张晓晖，韩昌元.光学系统计算机辅助装调中的一种优化算法［J］.光学 精密工程，2000，8(3)：273-277.ZHANG B，ZHANG X H，HAN CH Y.Algorithm for misalignmental determination in computer-aided alignment of optical system［J］.Opt．Precision Eng.，2000，8(3)：273-277.(in Chinese)

［4］ KATUSMI S，TETSUYA O，MURAKAMI K，et al..Assembly and alignment of three aspherical mirror optics for extreme ultraviolet projection lithography［J］.SPIE，2000，3997：751-758.

［5］ LEIGH D，FREIMAN D.Computer aided optical system with CODE VTM［J］.SPIE，1988，1038：288-294.

［6］ Optical Research Associates Inc.CODE V Reference Manual［M］.Pasadena：Optical Research Associates Inc，2003.

［7］ FISCHER R E，TADIC-GALEB B，YODER P R.Optical System Design［M］.Phoenix：Phoenix Book Tech.，2000：116-118.