基于窗口变换与多边形网格的三维井壁建模方法
陈志飞
(大庆油田测试技术服务分公司 黑龙江大庆)
基于窗口变换与多边形网格的三维井壁建模方法
陈志飞
(大庆油田测试技术服务分公司 黑龙江大庆)
在多臂井径测井资料转换中,物理窗口的测试点向量与物理窗口平移变换矩阵相乘,再与窗口缩放矩阵相乘,最后与屏幕显示平移变换矩阵相乘,得到了屏幕窗口显示点向量。将三维圆柱坐标系的任意点P(ρ,θ,Y)转换为笛卡尔坐标系形式,再以视角Ф将P投影到迪卡尔坐标系的一个坐标平面。该投影点可以通过窗口变换的方法转换到计算机显示屏幕窗口,将同一深度多独立臂井径所对应的多个点按上述方法转换到计算机屏幕显示窗口并连线就得到了该深度截面多边形。不同深度截面多边形在纵向上连接并将背面线消去就得到了基于多边形网格的三维井壁模型。
窗口变换;多边形网格;井壁建模
0 引 言
多臂井径测井被广泛应用于油水井套管检测,目前多臂井径测井资料解释软件很多,但详细介绍其井壁成像建模方法的很少。边界表示是一种常用的三维建模方法。很多图形系统以一组表面多边形来存储物体的描述。多面体的多边形表示精确地定义了物体的表面特征[1]。由于多边形网格线框轮廓能快速显示并且概要地说明表面结构,因此,这种表示在设计和实体模型应用中普遍采用。本文完整的介绍了一种基于多边形网格方法的多臂井径测井三维井壁建模方法。
1 基于窗口变换的二维向量处理
所谓建模,就是使用计算机以数学方法描述物体和它们之间的空间关系。本文所提的三维井壁建模就是指用数学方法将油水井多臂井径的测井数据转换到计算机屏幕(绘图纸)上,并正确还原油水井套管内壁的形态[2]。由测井文件所得到的数据是相应不同物理深度的若干组井径值纪录。将测井数据中某一深度某一井径值作为一个二维向量Pt(X,Y),将Pt转换到计算机显示屏幕窗口又得到了一个二维向量Ps(X1,Y1)。
测试数据到屏幕显示的转换可通过图形学中的窗口变换功能来实现。在计算机图形学中,通常用矩阵来对每个点进行变换,将一个点的向量与一系列变换矩阵相乘。测试点数据位于物理窗口中,对应的显示点在屏幕窗口中。在图1中一旦确定物理窗口范围和对应的屏幕窗口范围,设定Pt是测试点坐标向量;Ps是显示点坐标向量,为方便计算使用三维向量表示PtPs。测试点坐标到屏幕坐标的转换由下列变换得到:
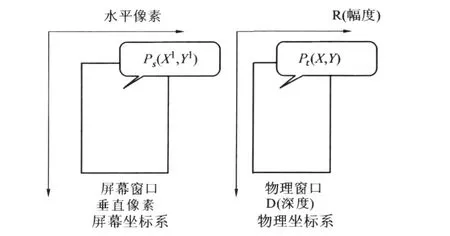
图1 测井数据窗口变换示意图
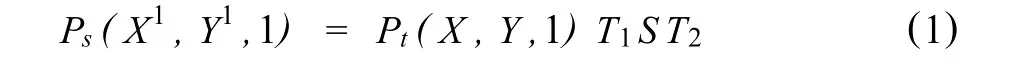
式(1)中
式(1)计算可得:
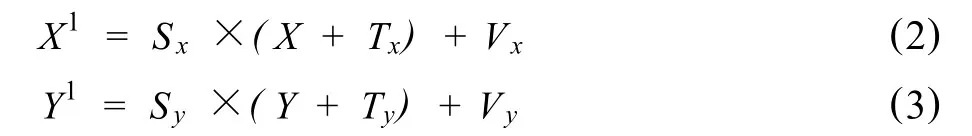
因为确定了物理窗口范围和对应的屏幕窗口范围,所以平移矩阵T1和T2均为已知。在设定了屏幕窗口的左右标尺值和纵向深度每米像素数后,缩放矩阵S也为已知。TxTy分别对应物理窗口坐标点的标尺值深度值,VxVy分别对应屏幕窗口坐标点的水平垂直像素值,Sx为屏幕窗口像素宽度与物理窗口标尺宽度之比,Sy为屏幕窗口像素高度与物理窗口深度差之比。
2 基于多边形网格的三维井壁建模
2.1 圆柱体在三维圆柱坐标系的数学转换
三维图形物体中运用边界表示的最普遍方式是使用一组包围物体内部的表面多边形。对于圆柱体的套管内壁,多边形线框轮廓能快速显示并概要地说明表面结构。因为套管井筒内部是标准的圆柱体,所以在对其描述的过程中使用了三维圆柱坐标系。一帧多臂井径数据可以看作是确定深度的一个多边形水平截面。
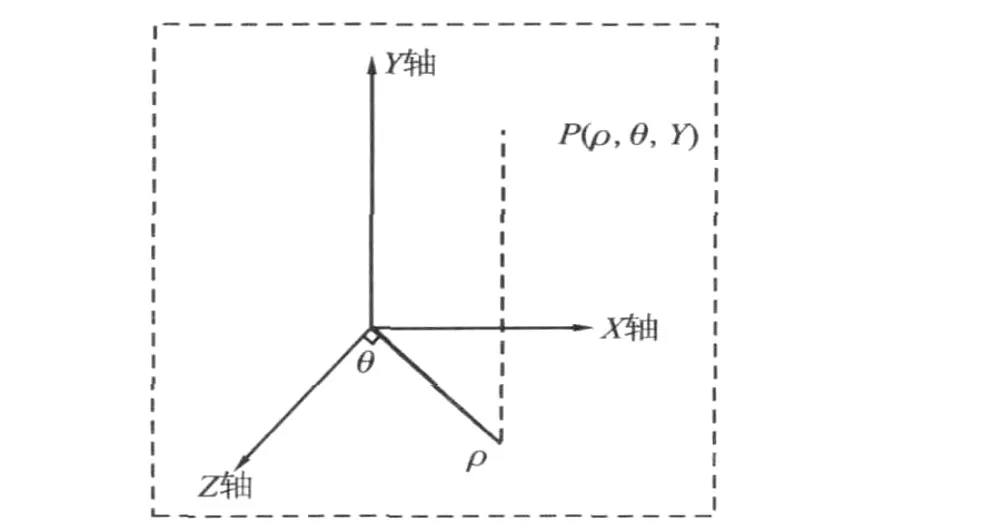
图2 三维圆柱坐标系[2]
图2就是三维圆柱坐标系的示意图,给出了空间位置的圆柱坐标描述,以及与笛卡尔参照系的关系,常数ρ的表面是一个垂直圆柱面,常数θ的表面是包含Y轴的垂直平面。而常数Y的表面是平行于笛卡尔ZX位平面的水平面。我们可由圆柱坐标描述变换到笛卡尔参照系:
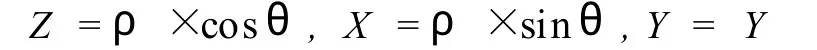
将三维的圆柱坐标系在二维计算机屏幕上显示需要将圆柱体投影在YZ平面或YX平面上。具体如图
产生实体的视图的一种方法是:将物体表面的点沿平行线投影到显示平面上,通过选择不同的观察位置,可以将物体上的可视点投影到显示平面上来。在图3中设定平行线与圆柱体的上表面夹角为Ф,则P(ρ,θ,Y)点在平面YX的投影点坐标P1(X,Y)的坐标为:

上一行的坐标描述中,Ф为给定常数即俯视视角,θ为井径臂与三维坐标系X轴的夹角,系统设定井径1与X轴的夹角为零度。ρ的物理意义是井径值。
由本文前面介绍的屏幕窗口物理窗口变换方法可以将P(ρ,θ,y)点在平面YX的投影点坐标P1(ρ×sinθ,Y+ρ×sinФ×cosθ)的坐标转换为屏幕坐标向量Ps(X1,Y1),公式如下:
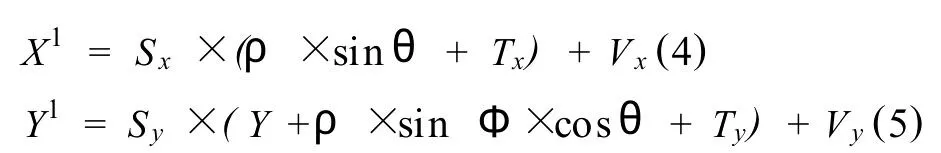
至此就可以方便的把某一深度一帧测井数据转换为投影在屏幕上的多个点,将这多个点顺序连线就得到一个多边形。以十六臂测井为例,当俯视角为π/6时标准套管截面投影到显示器屏幕上所得到的十六边形类似于短焦距为长焦距一半的椭圆,当俯视角为π/2时所得到的十六边形类似一个标准圆。
至此,单帧数据所反映的某一特定深度的套管水平截面的俯视图就已完成了,对十六臂井径资料来说,是以一个中心点每隔22.5°的十六个半径值的连接而成的十六边形以Φ为视角的俯视图。
2.2 用背面线消去的多边形网格建模方法
在套损井修井过程中,在多臂井径测井工序前,有一道重要工序是使用通井规通井。一般针对Φ139.7 mm壁厚7.72 mm规格的套管,使用Φ120 mm通井规,该套管标准内径为124.26 mm。由于通井规和连接所用的油管均为刚性物体,多臂井径仪也为刚性物体,可以近似认定测井过程中多臂井径仪的物理中心3所示。就是标准套管的垂直轴心[3]。鉴于这个事实,我们可以假定由每一帧井径数据转换的十六边形的中心点在纵向上位于同一直线上。将相邻每个十六边形同一条井径臂反映的点纵向相连,就得到了由多边形网格表示的套管内壁网格模型。

图3 圆柱体在观察平面YX上的投影
一般测井系统每米记录40个点,而计算机屏幕显示每米一般需要10个像素,所以转换到屏幕上的相邻检测点或者是相邻像素,或者是重迭像素,所以纵向上使用曲线拟合方法显示己没有必要。同样因为测井文件纵向采集点比较密,如果每一深度测量点都进行多边形相邻点连线,那么在视觉上所有连线将重叠在一起将看不到轮廓。在实际应用的解释系统中一般采取每隔0.5 m或0.3 m将同一深度的多边形连接。
图4是将背面线消去的某井套管段的多边形网格图。
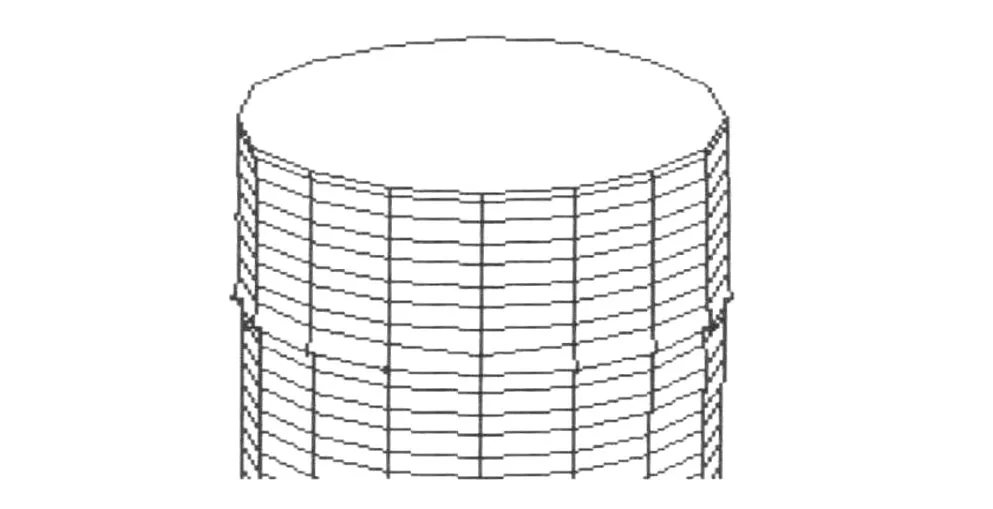
图4 背面线消去的某井段套管网格图
基于多边形网格建立的三维套管网格图可以快速客观地模拟套管内壁情况,结合被测量套管的基本参数(外径、壁厚)、各独立臂井径曲线和最大最小平均井径曲线可以对套管受损状况进行准确直观的分析。在图5中根据套管内壁网格图和井径曲线,可以准确判断在976.5到979.5井段套管已经缺失。
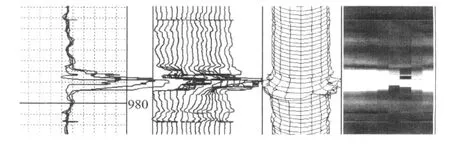
图5 结合了最大最小平均井径曲线、各独立臂井径曲线、三维套管网格图和灰度图的解释图
编程上,采取显示井径臂与隐藏井径臂依次更换的方法来实现井筒的旋转。在显示器上,三维网格图可以绕轴线以22.5°或者其倍数旋转,以便选择显示套损部位的较佳角度。
3 结束语
本文着重从数学角度推导了基于窗口变换的二维向量转换方法和基于多边形网格的三维井壁建模方法。给出了多个数据转换公式。其中窗口变换方法适用于所有线性测井曲线的屏幕显示应用。
本文所介绍的多边形网格模型应用的前提是所有多边形物理中心在纵向上位于同一条直线上。所显示的多边形网格为背面线消去的多边形网格,如果想显示被隐藏的一面,可以将显示井径臂与隐藏井径臂依次更换的方法实现井筒的旋转。该多边形网格井壁模型适用于十六臂、三十六臂、四十臂等所有多独立臂井径测井资料建模。
[1] Donald Hearn M.Pauline Baker著,蔡士杰,等译.计算机图形学[M].北京:电子工业出版社,1998
[2] 谭廷栋.测井学[M].北京:石油工业出版社,1998
[3] 陈相贵.生产测井[M].南充:西南石油学院出版社,1994
PI,2011,25(1):27~29
A point vector of physic window multiplied by transforming matrixes and scaling matrix,makes the point vector of screen window.When transferring a point P(ρ,θ,Y)form cylindrical coordinate system to cartesina system,we got a projection in one surface of cartesian coordinate system.This point matrix could be showed on the screen surface by window transformation method.When we transfer a frame well-logging data of multi-armed caliper to screen surface and line all the points,one polygon will be formed.When we link polygons of different frames,the well inner-surface model would be showed on the screen.
Key words:window transformation,polygon mesh,inner-surface model
The well inner-surface model based on window transformation and polygon mesh.
Chen Zhifei.
P631.8+1
B
1004-9134(2011)01-0027-03
陈志飞,男,1973年生,工程师,1996年毕业于西南石油学院测井专业,2006年获南京大学计算机技术工程硕士学位,现在大庆油田测试技术服务分公司从事测试工程定额管理工作。邮编:163412
2010-08-28编辑高红霞)

