0Cr11Ni2MoVNb钢高温流变应力的本构方程

王少刚，李庆华，李付国，魏志坚，苏春明

（1.西北工业大学 材料学院，陕西 西安 710072；2.中航工业安大航空锻造有限责任公司，贵州 安顺 561000）

0Cr11Ni2MoVNb钢高温流变应力的本构方程

王少刚1，李庆华1，李付国1，魏志坚2，苏春明2

（1.西北工业大学 材料学院，陕西 西安 710072；2.中航工业安大航空锻造有限责任公司，贵州 安顺 561000）

在Gleeble1500热模拟试验机上进行等温热模拟压缩试验，研究了0Cr11Ni2MoVNb钢在变形温度950℃～1100℃应变速率0.01～10s－1之间的热压缩变形行为。通常使用的本构模型，大多采用Z参数来表示温度和应变速率对材料变形行为的影响，而研究发现本构方程中材料常数是随着应变有规律性的变化，通过加入应变补偿，用与应变有关的多项式表示材料常数，这种方法建立的本构方程能够更精确的预测出材料在不同变形温度和应变速率下的应力值。

材料实验；流变应力；等温热模拟压缩；0Cr11Ni2MoVNb钢

1 前言

马氏体不锈钢是一类可以通过热处理（淬火、回火）对其性能进行调整的不锈钢，通俗地讲，是一类可硬化的不锈钢，具备高强度和耐蚀性。可以用来制造在较高温度下工作的零件，诸如蒸汽涡轮的叶片、蒸汽装备的轴和拉杆以及在腐蚀介质中工作的零件如活门、螺栓等[1，2]。0Cr11Ni2MoVNb 钢是一种新型马氏体热轧不锈钢，主要用于大型燃气轮机涡轮盘的制造。材料的本构方程是描述材料变形的基本信息，它表明了在热加工变形条件下流动应力与温度、应变速率以及应变之间的依赖关系。在制造涡轮盘的生产工艺研究中，本构方程是计算塑性变形过程的必要条件，为了更好的服务于工业生产，高效的生产出高质量的涡轮盘件，需要建立较为精确的材料高温下的热变形行为模型。

目前，研究金属材料本构方程较普遍的方法是使用双曲正弦函数，选取达到峰值应力时的应变，用Z参数表示温度、应变速率和应力三者之间的相互关系，忽略了应变对本构方程中材料常数的影响[3～5]。本文采用国内外一种新的方法[6～8]，加入应变补偿，建立温度、应变、应变速率和应力之间的本构关系，用来预测0Cr11Ni2MoVNb钢在高温下的变形行为。以此为目的，在热模拟压缩试验中控制应变速率和温度，获得材料的应力应变数据。

2 试验材料和方案

试验材料的化学成分见表1。压缩试样为ø8mm×10mm的圆柱体，两端加工有深0.2mm的浅槽，以便添加石墨润滑剂，保证压缩变形的均匀性和稳定性。试验在Gleeble1500热模拟试验机上进行，试样采用电磁感应加热至1200℃，保温3min，待试样充分奥氏体化后，再以5℃/s速度冷却至变形温度，以等温恒定应变速率压缩，变形终止后立即淬水冷却至室温。变形温度分别为950℃、1000℃、1050℃、1100℃，应变速率为 0.01s－1、0.1s－1、1s－1、10s－1。由试验机的控制计算机自动采集应力、应变、压力、位移、温度及时间等数据，绘制应力—应变曲线。

表1 0Cr11Ni2MoVNb钢的化学成分wt/%

3 试验结果与分析

0Cr11Ni2MoVNb钢高温压缩变形时不同变形温度和应变速率下的应力—应变曲线见图1。从图中可见，0Cr11Ni2MoVNb钢在高温变形条件下的流变应力曲线有两种形式，一种是高应变速率、低变形温度的情况下，呈现出动态回复；另一种是低应变速率、高变形温度的情况下出现动态再结晶型。试验结果表明，在应变速率低于0.1s－1且温度高于1000℃时，应力—应变曲线随着应变的增加，应力达到峰值，随后出现软化，为典型的动态再结晶曲线，与文献[5]中的结论基本一致。

材料在高温下的流动应力、温度和应变速率之间的相互关系一般常用式（1）、式（2）表达，而 Zener－Holloman（Z）参数是温度和应变速率对材料的变形行为影响的重要参数。

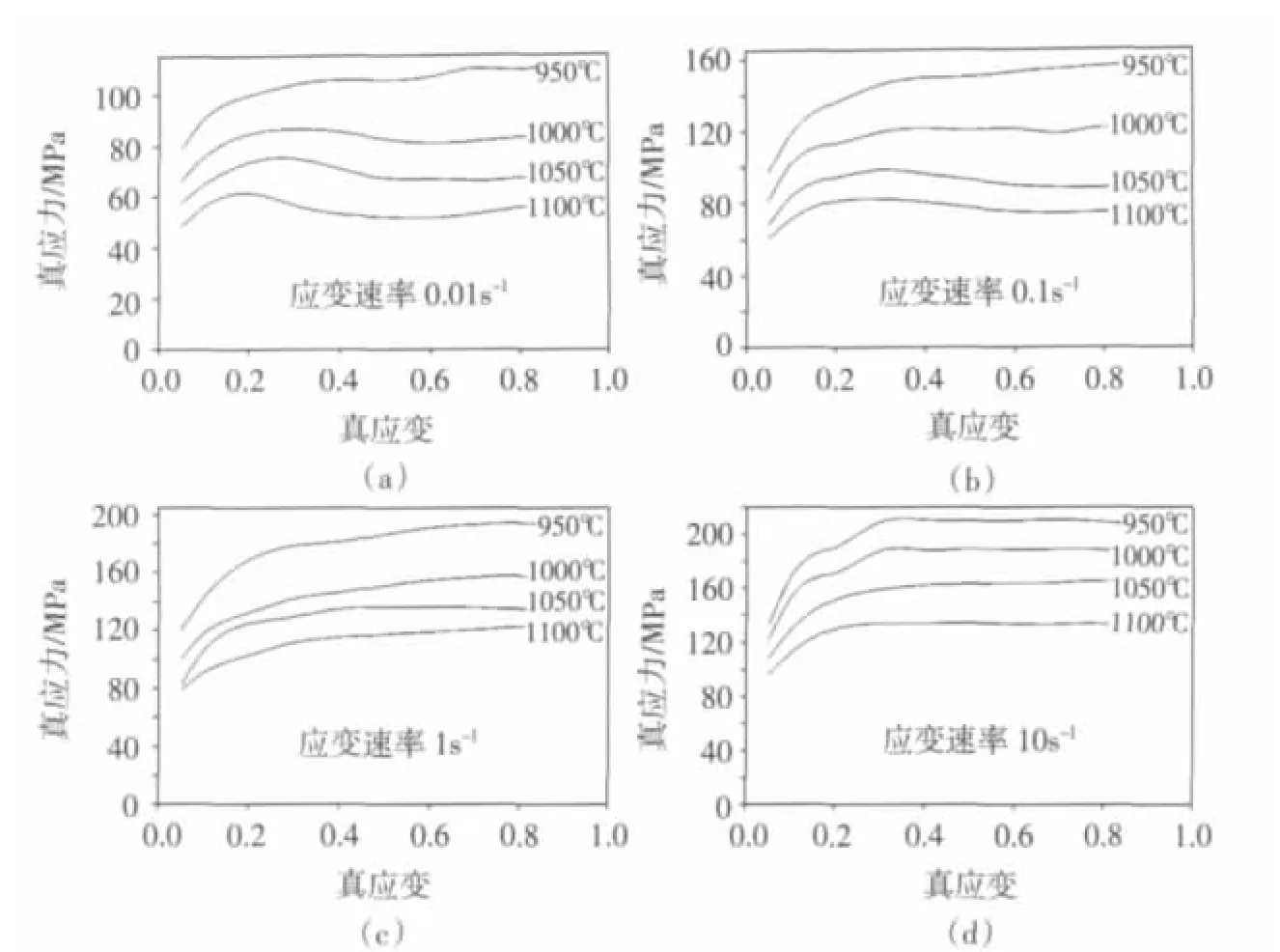
图1 应力—应变曲线

对于低应力和高应力水平下，可将上式写为：

对式（3）和式（4）两边分别取对数得：

根据不同条件下的应力值分别建立 ln（σ）-ln（ε˙）和 σ-ln（ε˙）关系图，通过线性拟合计算得到其中某个应变下的不同n1和β值，取平均值得到该应变条件下的n1和β。以应变ε=0.3为例，图2为 ln（σ）—ln（ε˙）和 σ—ln（ε˙）关系图。

计算得到平均值 n1=8.9306975，β =0.0759925，α =β /n1=0.008509134。

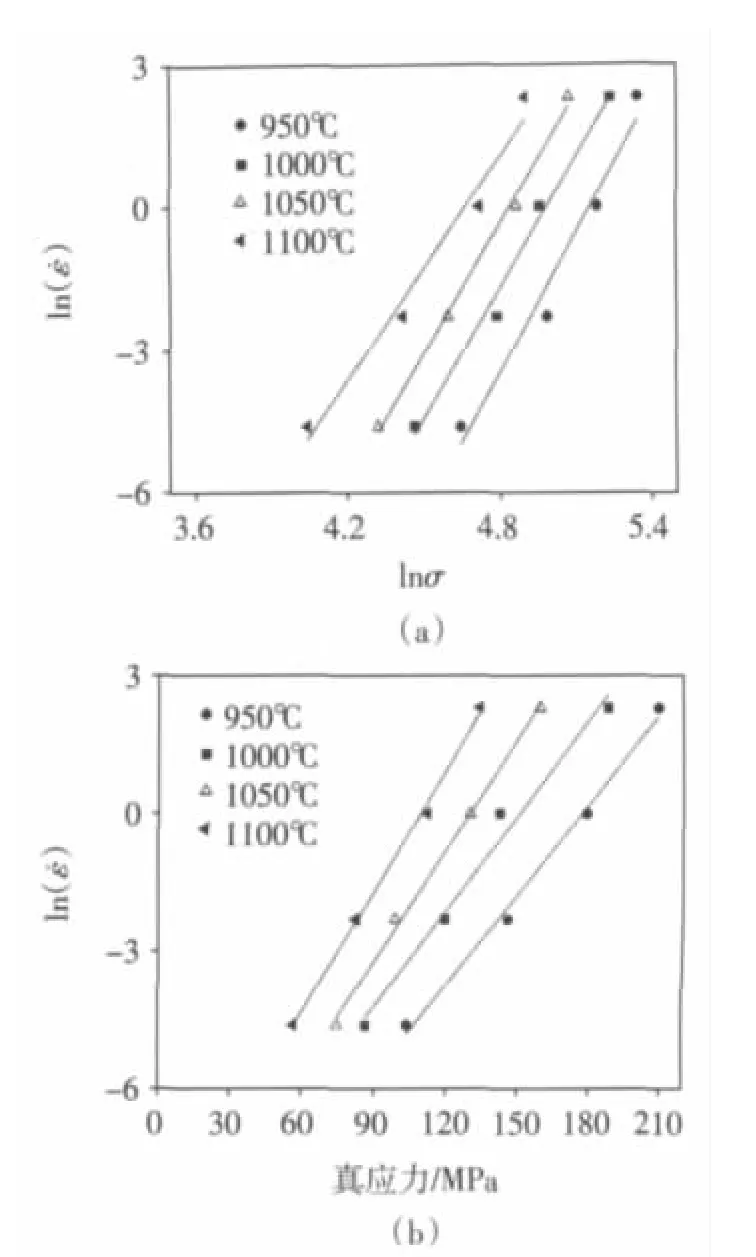
图2 应变为0.3时的n1和β值的估计

对所有应力水平下（包括高应力和低应力），应力、应变速率以及温度的相互关系可用下式表示：

分别对等式两边取对数，可得：

对于给定的应变速率下，根据式（7），可以得到：

因此，在四种不同应变速率的条件下，代入不同的温度流动应力到式（9）中，可以得到 ln（sinh（ασ））与温度T的相互关系，如图3a所示。Q值来源于ln（sinh（ασ））-1/T的斜率，同一应变不同应变速率下的Q值取平均得到该应变下的变形激活能Q，当ε=0.3 时，Q=432.078kJ·mol-1。

图3 Q与lnA值的估计

A的值是在特定的应变下，通过ln[sinh（ασ）]-lnε˙曲线获得，如图3b所示，在应变为0.3时 A=1.8926×1016。

按照上述方法，同理可求得所有应变条件下（0.05～0.85）的 α、n、Q、lnA 的值，然后用五次多项式对其进行拟合：

拟合结果如图4所示，由图中可以看出，材料常数都随着应变的变化呈现出规律性的变化，通过多项式拟合，可以更精确的表达出不同应变下的材料常数值。

计算得到上述表达材料常数的多项式各项系数，见表2。

对于流动应力σ代入Z参数表示，根据式（7）可写成如下表达式：

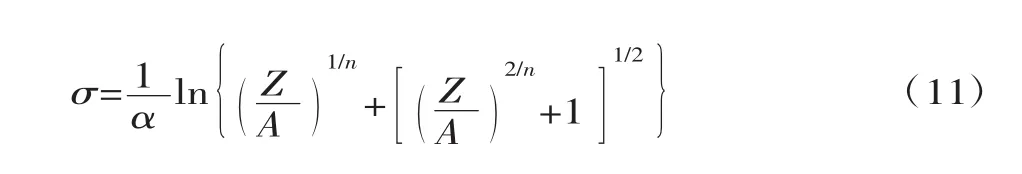
通过上述多项式计算出不同应变下的α、A、n和Q值，再通过Q计算出不同条件下的Z值，代入式（11），计算得到不同温度、应变速率和应变时的应力值σ，并与实验得到的应力值相比较，如图5所示。从图中可以看出，应变速率为（0.01～1）s－1时，实验值与计算得到的预测值比较吻合。当应变速率为10s－1、应变大于 0.4 时，误差比较大，这是因为应变速率较高时，变形过快，材料内部形成绝热剪切带引起的[9]。

4 本构方程的验证

试验值与计算出来的本构方程的预测值之间的比较如图6所示，本构方程的准确性通过统计参数相关系数（R）和绝对误差的平均值（AARE）进行验证，其计算公式如下：

式中：E——试验值；

P——由本构方程得到的预测值；

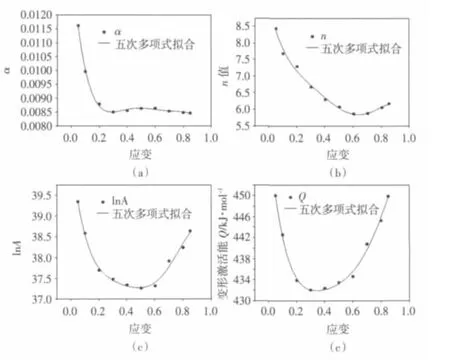
图4 α、n、lnA、Q随应变变化的五次多项式拟合曲线

表2 五次多项式系数值

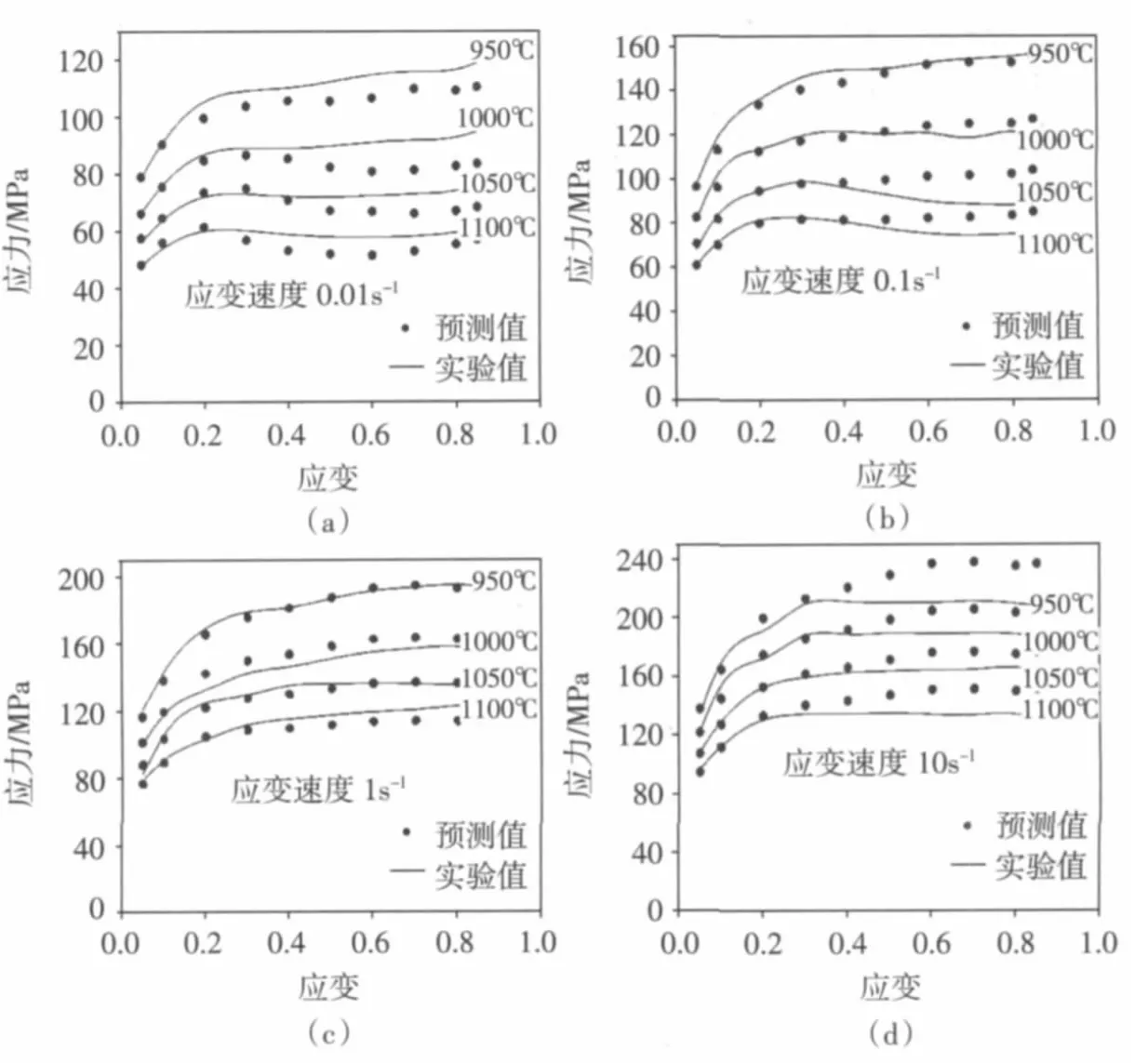
图5不同应变速率下实验值与预测值的应力—应变曲线

N——所研究数据点的数量，相关系数是一种常见的统计学参数。

由图6可以看出，试验值与预测值之间有很好的相关性，在应力值较大时，即变形温度低、高应变速率的条件下，尽管有些散射，但AARE值仅为5.03%，证明了本构方程能够很好的预测真实应力大小。

图6 试验值与预测值之间的相关性

5 结论

对0Cr11Ni2MoVNb钢进行了热模拟压缩试验，研究了其流变行为，分析计算获得该材料的本构方程，得到以下结论：

（1）在本构分析中，综合考虑了应变对材料常数的影响（包括α、n、lnA、Q等），用与应变有关的五次多项式表示本构方程中的材料常数，并具有很好的相关性和普遍性。

（2）考虑了应变补偿的本构方程能够准确预测出不同温度和应变速率条件下的应力值，虽有些区域有一定偏差，但仍在允许的误差范围内，能较好反应出材料应力—应变曲线的变化规律和特征。

[1]K.H.Lo，C.H.Shek，J.K.L.Lai.Recent developments in stainless steels[J].Materials Science and Engineering：R，2009，65（4-6）:39-104.

[2] C.Müller-Bollenhagen，M.Zimmermann，H.-J.ChristC.M u¨ller-Bollenhagen，M.Zimmermann，H.-J.Christ.Adjusting the very high cycle fatigue properties of a metastable austenitic stainless steel by means of the martensite content[J].Procedia Engineering，2010，2：1663-1672.

[3] 孙付涛，陈拂晓，郭俊卿，韩 晨.铸态AZ31B镁合金热压缩流变应力[J].锻压装备与制造技术，2008，43（3）:73-76.

[4] 盛永华，王新云，夏巨谌.7475铝合金高温高应变速率压缩变形的流变应力[J].锻压装备与制造技术，2005，40（4）:98-100.

[5] 王立民，张 红，吕成林，邰青安，王照坤，杨 钢，刘正东.0Cr11Ni2MoVNb钢高温压缩变形的流变应力[J].金属学热处理，2008，33（10）：74-76.

[6] Y.C.Lin，Ming-Song Chen，Jue Zhong Effect of temperature and strain rate on the compressive deformation behavior of 42CrMo steel[J]，Journal of Materials Processing Technology，2008，205 （1-3）:308-315.

[7]Sumantra Mandal，V.Rakesh，P.V.Sivaprasad，S.Venugopal，K.V.Kasiviswanathan.Constitutive equations to predict high temperature flow stress in a Ti-modified austenitic stainless steel[J]，Materials Science and Engineering：A，2009，500（1-2）:114-121.

[8] Y.C.Lin，Ming-Song Chen，Jue Zhong.Constitutive modeling for elevatedtemperatureflowbehaviorof42CrMosteel[J]，Computational MaterialsScience，2008，42（3）:470-477.

[9] Y.C.Lin，Ming-Song Chena，Jue Zhong Prediction of 42CrMo steel flow stress at high temperature and strain rate[J]，Mechanics Research Communications，2008，35，（3）：142-150.

Constitutive Equations to High Temperature Flow Stress of 0Cr11Ni2MoVNb Stainless Steel

WANG Shaogang1，LI Qinghua1，LI Fuguo1，WEI Zhijian2，SU Chunming2
（1.School of Materials Science and Engineering，Northwestern Polytechnical University，Xi'an 710072，Shanxi China；2.AVIC Guizhou ANDA Aviation Forging Co.，Ltd.，Anshun 561000，Guizhou China）

The compressive deformation behavior of 0Cr11Ni2MoVNb steel has been investigated during the temperatures from 950℃ to 1100℃ and strain rates from 0.01 to 10s-1on Gleeble-1500 thermo-simulation machine.The effects of temperature and strain rate on deformation behaviors have been represented by Zener-Holloman parameter in an exponent type equation,but in fact material constants change regularly with strains.The influence of strain has been incorporated in the constitutive analysis by considering the effect of strain on material constants.The constitutive equation （considering the compensation of strain）could precisely predict the flow stress in different temperatures and strain rates.

0Cr11Ni2MoVNb steel；Flow stress；Compensation of strain；Constitutive equation

TG142.71

A

1672－0121(2011)01－0091－04

2010－10－25

王少刚（1986－），男，硕士在读，主攻材料塑性加工与控制