金融机构与企业在技术创新中的利益分配
——基于罗宾斯坦恩博弈模型
柯桂丹,杜丽娟
(河北联合大学,河北唐山063009)
金融机构与企业在技术创新中的利益分配
——基于罗宾斯坦恩博弈模型
柯桂丹,杜丽娟
(河北联合大学,河北唐山063009)
技术创新;利益分配;讨价还价博弈
建立公平合理的利益风险机制,以促进金融对企业技术创新的支持。通过修正的罗宾斯坦恩讨价还价模型对技术创新活动中金融机构和企业的合作关系进行描述,建立了完全信息下金融机构与企业的合作博弈模型,提出了金融机构支持企业技术创新的利益分配方法,为实现金融机构与企业在技术创新上合作利益的合理分配提供方法支持。
企业技术创新活动本身就是高风险与高收益并存,金融机构提供资金支持企业创新,属于不同利益主体之间的合作,与单一利益主体的技术创新相比,既增加了合作中的风险,又增加了利益分配上的复杂性。商业银行的一切经营活动均要服从盈利性和安全性的目标,双方技术创新合作的利益分配问题更显得复杂且重要。对风险分摊、利益分配问题处理得当,就会大大增加双方合作创新的积极性,从一定程度上保证合作的成功;否则,就会削弱合作的动力,甚至导致合作的失败。因此,金融机构与企业合作创新必须建立合理的创新利益分配机制,博弈论中的合作博弈为这种利益分配提供了理论指导。
企业与金融机构在选择合作项目时,一般会先分析自身对项目的投入、收益,以及项目存在的风险,然后通过谈判(博弈)寻求参与者各自所要承担的责任,以及所能取得的收益,只有确定预期承担的风险和获得的收益对等才存在合作的可能性。根据纳什定律,所有的博弈都存在均衡状态,即对于博弈所有参与者站在各自立场上基于理性考虑的最佳结果。因此只有建立在纳什均衡策略上的合作才是双赢的,否则必有一方受损,合作就不稳定。
科技与金融的结合可以看作合作项目的利益相关者之间基于投资、收益的博弈,而有效的合作是建立在这种博弈模型的均衡状态基础上的。本文尝试利用著名的谈判模型—罗宾斯坦恩讨价还价博弈模型来分析企业和金融机构在技术创新活动中的博弈关系,得出该博弈模型下的均衡状态,并在此基础上提出企业和金融机构合作的利益分配方案,实现利益相关方之间的帕累托最优。
一 完全信息下轮流出价讨价还价模型
埃奇沃斯(Edgeworth,1881)创造了著名的“埃奇沃斯盒形图”用以展示讨价还价的可能结果的范围,但却不能提供唯一的解,其后,泽塞(Zeuthen,1930)与希克斯(Hicks,1932)对讨价还价做了定义,并在两方面进行了发展,一方面对讨价还价做出了一种通俗的描述,另一方面对可能导致什么样的结果做出了明确的预测[1]。纳什(Nash,1950,1951)提出了任何合理的讨价还价解都应该遵守的公理,并指出最大化行为人的效用的乘积是唯一满足他的公理的解(纳什讨价还价解)[2]。但是,以上理论体系都是静态的,缺少对合作博弈的过程分析,宾莫尔、罗宾斯坦恩与沃林斯基证明出,轮流出价的非合作博弈的子博弈完美均衡与纳什讨价还价所描述的效用乘积最大化相一致。
马克·罗宾斯坦恩(Mark Rubinstein)用完全信息动态博弈的方法,对基本的、无限期的完全信息讨价还价过程进行了模拟,并据此建立了完全信息轮流出价讨价还价模型。
(一)罗宾斯坦恩博弈模型
在完全信息下,合作项目s的可分配收益为U,利益相关方甲、乙共享这份收益。博弈的参与方都具有“个人理性”即追求自身利益最大化。假设在时间t=1,利益相关者甲提议自己要求得到x1,留x2给另一方乙。如果乙接受甲的提议,则博弈结束,甲和乙得到的收益分别为(x1,x2)。但乙可能认为甲的方案不公平而拒绝接受并提出反提议,此时t=2,轮到甲做选择,若甲同意,则甲和乙获得的收益分别为(δx1,δx2),若甲不同意再继续提出反提议,如此下去直到双方达成一致。根据无限期罗宾斯坦恩讨价还价博弈模型,存在的唯一的均衡收益分配(珔u,珋v)。
乙的收益为:
(二)引入外部选项的罗宾斯坦恩博弈模型
对于合作参与者只有一个项目,或者各方进行同一个项目时,罗宾斯坦恩讨价还价模型可以很容易解决各利益相关方的利益分配问题。然而现实中普遍存在的情况是多个参与者同时进行多个项目,由于每个参与者都具有个人理性,就可能为了达到个人收益最大化而放弃当前合作项目。即在存在外部威胁的情况下,参与者不同意提议时,除了反提议之外还可以选择放弃。此时,需要在罗宾斯坦恩博弈模型的基础上加入表示外部机会收益的变量x01,x02。
金融机构和企业除了科技创新活动合作项目以外,同时还可能进行多个其他投资项目(假设企业同时进行项目S和项目C、D,金融机构进行着项目 S和E、F),同时由于资金、设备等资源的有限性,而各参与者都有追求自身利益最大化的意愿,存在将资源投入其他项目而获得相应的外部收益的可能性,结果很可能是合作参与者将关键资源投入到其他项目获取自身最大收益,而该合作项目由于关键资源无法到位,而导致失败。此时,对于讨价还价博弈中的利益相关方来说,该外部收益相当于博弈参与者给予对方的一种威胁。
本文将分析存在外部威胁时,罗宾斯坦恩博弈模型在企业与金融机构合作创新这一问题上的应用扩展。
二 完全信息下金融机构与企业在技术创新中的合作博弈
任何合作都必须以提高双方的收益为条件。对利益相关方而言,应存在着具有帕累托改进性质的分配规则,即合作所创造的利益至少应不低于不合作时所创造的利益。因此,利益相关方才会采取合作的策略,以获得更多的收益。
(一)科技创新活动合作博弈的变量设置
1.S——可行方案集
科技创新中的合作表现为企业和金融机构之间(甲乙方)的博弈,他们提出自己的要求以及相应措施。这些方案在实际中应该总是可行的,所有这些可行方案构成的集合称为可行集,记为S。
2.(u,v)—方案
在每个方案中,博弈双方分别获得的收益记为u、v,将每个方案表示为(u,v),并且写作(u,v)∈S,这代表着方案(u,v)是可行的。双方都有一个谈判的基点,即双方认为都不能再让步的收益,假设甲乙方分别以(u0,v0)为基础进行博弈,即博弈双方的最小期望收益组合为(u0,v0)。
这样我们将谈判问题可以记作(S,u0,v0),经过博弈双方的讨价还价,得到一个双方都能接受的方案(珔u,珋v)。由(S,u0,v0)到最后的过程看作一种映射,记作映射φ。于是此过程可写作为谈判解[3]。
3.x1,x2—讨价还价过程中提议的收益
x1,x2为讨价还价过程中出现的变量。
5.us—合作项目S分配收益
在科技创新合作项目S结束时,项目中利益相关方甲乙之间要进行收益分配,设项目总的分配收益为us,将区间(0,作为整体来考虑,则就相当于模型中待分配的蛋糕,经过讨价还价,双方会在(珔u,珋v)处达到均衡,使得
6.δ—折扣因子
折扣因子反映了合作项目中参与方对于收益分配的迫不及待的程度,0≤δ≤1。若δ=O,说明迫切程度非常强烈,此时博弈便瓦解为一种一个期间的最后通碟博弈,若δ=1,说明参与者具有足够的耐心,因而出现多阶段博弈情形。折扣因子δ反映了讨价还价能力。在实践中,讨价还价能力的大小难以估算,现有文献对合作中企业讨价还价能力及其刻画指标的研究很少,没有合适的、现成的讨价还价能力指标可借鉴,但企业讨价还价能力在决策地位和竞争能力中可以体现出来。[4]
(二)加入外部威胁的完全信息博弈模型扩展
不存在外部威胁时,根据罗宾斯坦恩博弈模型可知,企业和金融机构的利益分配为(珔us,珋vs),其中

若引入外部选项,由于利益相关者甲(企业)不仅进行项目S,而且可能同时进行项目C和D,同时利益相关者乙(金融机构)不仅进行着项目S,可能同时进行着项目E、F等等。由于模型中利益相关者都是理性人,在资源有限的情况下,企业和金融机构都会追求个人利益最大化,若从项目S中得到的收益小于把资源投入项目S的机会收益,则双方都存在将资源转投至其他项目的可能性,从而导致项目S的失败。
假设金融机构综合考虑现在进行的所有项目,即项目S和项目E、F,在对各项目综合评估后,决定将关键资源投入到项目E或F中,则可以获得x02的机会收益,而此时,合作方企业由于缺少金融机构对合作项目S关键资源的投入而无法获得项目收益,那么此时甲、乙(即企业、金融机构)的收益组合为(0,x02)。同样,若企业选择将资源投入到其他项目C或D中,存在同样的情形,此时甲、乙的收益组合为(x01,0)。
若博弈确实能够进行,那么甲和乙必须在博弈中能够使自己的所得有所增加,即和存在以下关系:

的必要条件,而不是充分条件。因为存在以下几种情形,假设不存在外部机会收益的情况下达成的唯一均衡为(珔us,珋vs):
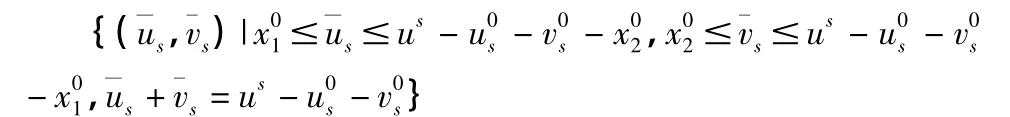

根据以上分析可得以下几种状态下的均衡状态:
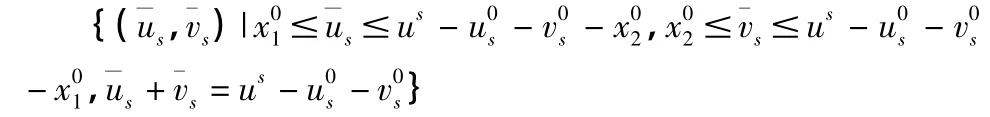
我们假设U=us-u0s-v0s,则此时企业和金融机构的收益分配关系如下:

三结论
本文在完全信息下的罗宾斯坦恩的讨价还价模型基础上,对技术创新活动中金融机构与企业的合作关系进行研究并建立扩展模型,分析了存在外部机会威胁时企业与金融机构在技术创新合作中的利益分配的均衡解,为实现金融机构与企业合作创新利益的合理分配提供方法支持和参考。但是,对于合作的利益相关方而言,外部机会收益的信息有可能是不对称的,因此,金融机构支持企业技术创新,在不完全信息条件下双方利益分配的博弈会出现在什么情况需要进一步深入研究。
[1] Mare M.Fuzzy Cooperative Games:Cooperation with Vague Expectations[M].New York:Physical-Verlag Press,2001.
[2] Oviedo Jorge.Core of a repeated n-person cooperative game[J].European Journal of Operational Research,2000(3).
[3] Jean - Claude Hemet;Sonia Mahjoub.2010.Toward the fair sharing of profit in a supply network formation.International journal of production economics.
[4] 洪银兴.合作博弈和企业治理结构的完善[J].南京大学学报:哲学、人文科学、社会科学,2003,40(3):21~27.
[5] 刘浪,唐海军,陈仲君.shapley值在动态联盟利益分配博弈分析中的应用[J].工业工程,2006(9):118~121.
[6] 科林·凯莫勒著.行为博弈—对策略互动的实验研究[M].北京:中国人民大学出版社,2006:162.
[7] 张维迎.博弈论与信息经济学[M].上海:上海三联出版社,2005:3
[8] 郭咸纲.多维博弈人性假设一理论管理学前沿课题研究[M].广州:广东经济出版社,2003:112~113.
[9] 李忠云,龙勇,张宗益.技能型战略联盟合作效应和企业讨价还价能力实证研究[J].中国软科学,2004(12):58~64.
[10] 房宏琳.讨价还价模型:在企业并购价格谈判中的应用[J].学术交流,2002(11):20.
F830.9
A
1673-2804(2011)06-0053-03
2011-03-29
河北省科技厅计划项目,《河北省科技与金融相结合的机制与对策研究》,科研编号(11457201D-33),本文为该科研项目的阶段性成果。

