原子玻色-爱因斯坦凝聚体对V型三能级原子激光压缩性质的影响*

李明

原子玻色-爱因斯坦凝聚体对V型三能级原子激光压缩性质的影响*

李明

(桂林理工大学理学院，桂林541004)
(2010年9月19日收到;2011年1月13日收到修改稿)

利用格子液体方法对V型三能级原子玻色-爱因斯坦凝聚体与双模压缩相干态光场相互作用系统的哈密顿量进行分析，发现文献中对原子间相互作用部分的处理有不合理之处，从而对该哈密顿量作出了改进并研究了V型三能级原子玻色-爱因斯坦凝聚体与双模压缩相干态光场相互作用系统中原子激光的两个正交分量的压缩性质．研究表明:V型三能级原子玻色-爱因斯坦凝聚体中光场-原子相互作用强度对原子激光的两正交分量的涨落有明显的影响．

玻色-爱因斯坦凝聚，V型三能级原子，压缩相干态，压缩原子激光

PACS:32.80.QK，42.50.－p

1.引言

玻色-爱因斯坦凝聚(Bose-Einstein condensation，简称为BEC)作为一种新的物质形态，从1995年在碱金属原子稀薄气体中实现以来，引起了研究的热潮［1—3］．随后不久，理论物理学家就预言从超冷的原子BEC中可以发射类似于激光的相干原子束．1997年，Ketterle小组［4］和Anderson等［5］相继获得了“原子激光”．此后，人们对原子激光的产生及其性质做了大量的研究，取得了一系列重要成果［6—18］．

在文献［19］基础上，利用格子液体方法［20］对光场-原子BEC系统的总哈密顿量进行了分析和改进，并讨论了原子玻色-爱因斯坦凝聚体对V型三能级原子激光压缩性质的影响．结果表明:BEC中光场-原子相互作用强度ε对原子激光的两正交分量的涨落有明显的影响．当ε较小时，Q1(t)呈非周期性变化，且压缩深度较浅．当ε较大时，Q1(t)呈周期性变化较明显，且压缩深度变深．

2.系统哈密顿量的改进和运动方程的求解

在熟知的Bogoliubov近似下［21］，文献［19］已推导出V型三能级原子的BEC与双模压缩相干态光场相互作用的系统的总哈密顿量

通过文献［22］分析可知(1)式中Ω对应于u0/2 Nc，于是得到改进后的哈密顿量

在共振条件(ω1=ω01，ω2=ω02)下，求解系统的Heisenberg运动方程［23］

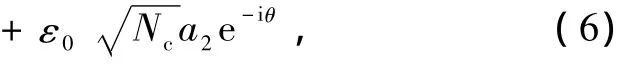
得到

3.原子激光的压缩效应

为了研究原子激光的压缩效应，定义原子激光的两个缓变的正交分量算符

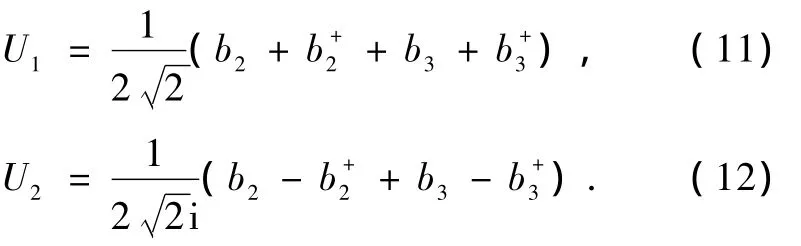
U1，U2满足下列对易关系

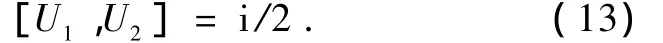
相应的不确定关系为

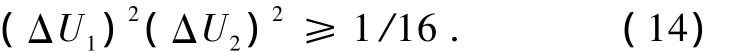
引入

可以得到

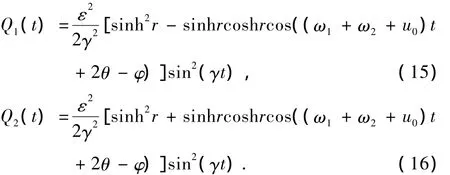
由于Q1(t)和Q2(t)的函数关系对称，只利用(15)式对Q1(t)作了计算和分析，取r=0.5，Nc= 105，ω1=100，ω2=110，ε0=2，z=10，u0=zε0=20．对ε考虑了光与原子作用强度不同的3种情况，即ε=0.005 u0，0.05 u0和0.5 u0．所得结果如图1所示．

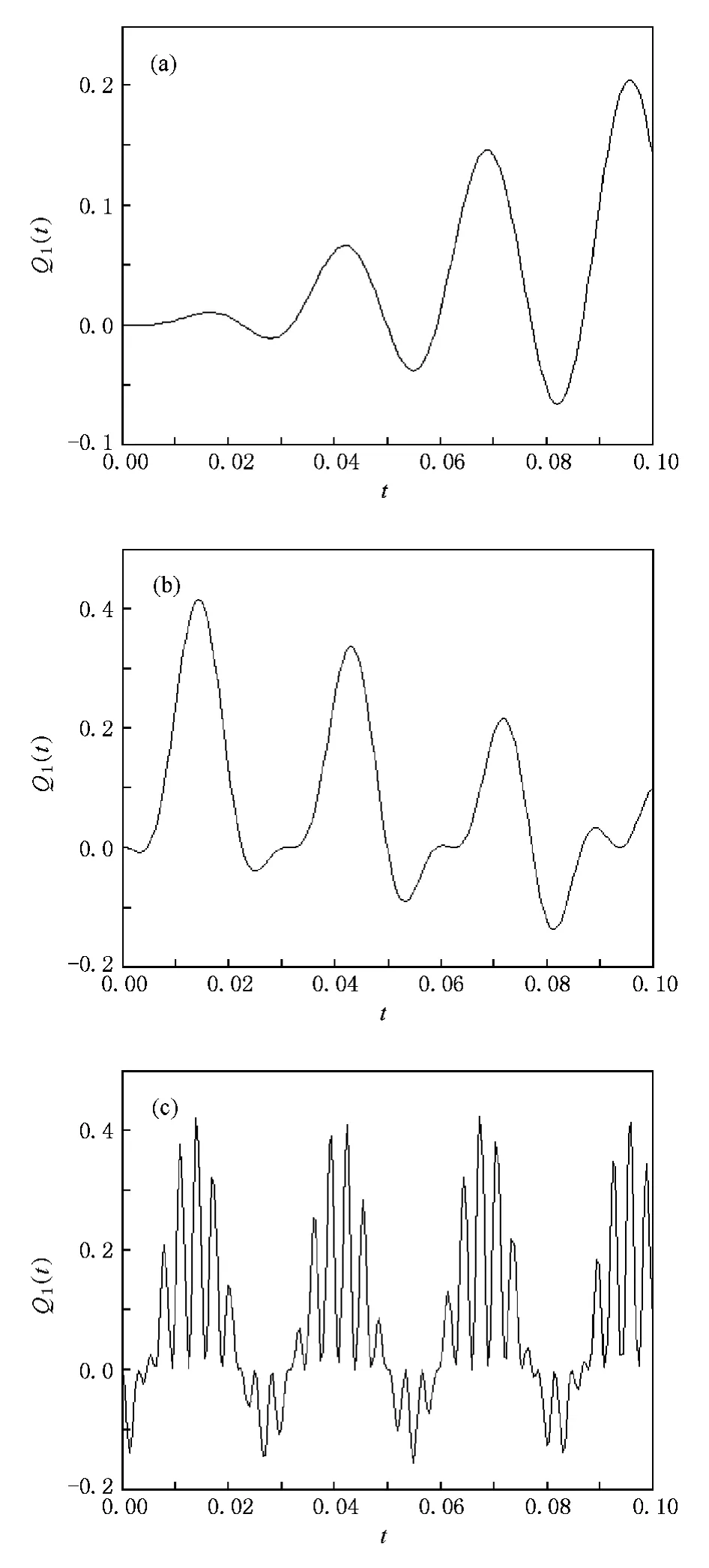
图1 原子激光Q1(t)的时间演化特性(a)ε=0.005 u0;(b)ε =0.05 u0;(c)ε=0.5 u0

从图1可以看出，BEC中光场-原子相互作用强度ε对原子激光的两正交分量的涨落有明显的影响．当ε较小时，Q1(t)呈非周期性变化，且压缩深度较浅．当ε较大时，Q1(t)呈周期性变化较明显，且压缩深度变深．这与(15)式是一致的．

4.结论

利用格子液体方法，对文献中给出的V型三能级原子玻色-爱因斯坦凝聚体与双模压缩相干态光场相互作用系统的哈密顿量进行分析，表明文献中对原子间相互作用部分的处理有不合理之处，从而对该哈密顿量作出了改进并进一步讨论了原子玻色-爱因斯坦凝聚体对V型三能级原子激光压缩性质的影响．结果表明:BEC中光场-原子相互作用强度ε对原子激光的两正交分量的涨落有明显的影响．当ε较小时，Q1(t)呈非周期性变化，且压缩深度较浅．当ε较大时，Q1(t)呈周期性变化较明显，且压缩深度变深．即在光场的初始压缩因子r，u0以及处于基态的超冷原子数目一定的情况下，BEC中光场-原子间的相互作用ε越强，原子激光的压缩深度越大．

［1］Anderson M H，Ensher J R，Matthews M R，Wieman C E 1995 Science 269 198

［2］Davis K B，Mewes M O，Andrews M R，Druten N J，Durfee D S，Kurn D M，Ketterle W 1995 Phys．Rev．Lett．75 3969

［3］Bradley C C，Sackett C A，Tollett J J，Hulet R G 1995 Phys．Rev．Lett．75 1687

［4］Mewes M O，Andrews M R，Kurn D M，Durfee D S，Townsend C G，Ketterle W 1997 Phys．Rev．Lett．78 582

［5］Anderson B P，Kasevich M A 1998 Science 282 1686

［6］Kuang L M 1998 Commun．Theor．Phys．30 161

［7］Kuang L M，Ouyang Z W 2000 Phys．Rev．A 61 023604

［8］Zhao Z C，Kuang L M 2000 Acta Sin．Quant．Opt．6 29(in Chinese)［赵志超、匡乐满2000量子光学学报6 29］

［9］You L，Lewenstein M，Cooper J 1995 Phys．Rev．A 51 4712

［10］Sun C P，Zhan H，Miao Y X，Li J M 1998 Commun．Theor．Phys．29 161

［11］Jing H，Chen J L，Ge M L 2001 Phys．Rev．A 63 15601

［12］Zhou M，Huang C J 2002 Acta Phys．Sin．51 2514(in Chinese)［周明、黄春佳2002物理学报51 2514］

［13］Zhou M，Fang J Y，Huang C J 2003 Acta Phys．Sin．52 1916 (in Chinese)［周明、方家元、黄春佳2003物理学报52 1916］

［14］Zhou M，Huang C J 2004 Acta Phys．Sin．53 0054(in Chinese)［周明、黄春佳2004物理学报53 0054］

［15］Zhang J M，Liu W M，Zhou D L 2008 Phys．Rev．A 77 033620

［16］Li Z G，Fei S M，Wang Z D，Liu W M 2009 Phys．Rev．A 79 024303

［17］Li Z G，Fei S M，Albeverio S，Liu W M 2009 Phys．Rev．A 80 034301

［18］Li Z G，Zhao M J，Fei S M，Liu W M 2010 Phys．Rev．A 81 042312

［19］Zhou Y X，Xia Q F，Sun C Y 2008 J．At．Mol．Phys．25 0633 (in Chinese)［周玉欣、夏庆峰、孙长勇2008原子与分子物理学报25 0633］

［20］Hu Y 1982 Molecular Thermodynamics on Fluids(Beijing: Higher Education Press)p380(in Chinese)［胡英1982流体的分子热力学(北京:高等教育出版社)第380页］

［21］Ni G J，Chen S Q 2000 Advanced Quantum Mechanics (Shanghai:Fudan University Press)p372(in Chinese)［倪光炯、陈苏卿2000高等量子力学(上海:复旦大学出版社)第372页］

［22］Li M，Sun J X 2006 Acta Phys．Sin．55 2702(in Chinese)［李明、孙久勋2006物理学报55 2702］

［23］Peng J S，Li G X 1996 Introduction of Modern Quantum Optics (Beijing:Science Press)p185(in Chinese)［彭金生、李高翔1996近代量子光学导论(北京:科学出版社)第185页］

PACS:32.80.QK，42.50.－p

*Project supported by the Key Project of Ministry of Education，China(Grant No．209094)and the Natural Science Foundation of Guangxi Province，China(Grant No．2010 GXNSFB013050)．

E-mail:liming@glite．edu．cn

Influence of an atomic Bose-Einstein condensate on the squeezing properties of V-type three-level atomic lasers*

Li Ming
(Department of Mathematics and Physics，Guilin University of Technology，Guilin 541004，China)
(Received 19 September 2010;revised manuscript received 13 January 2011)

The Hamiltonian operator of a system of V-type three-level atomic Bose-Einstein condensation interacting with twomode squeezed coherent light field is analyzed in terms of the lattice-liquid model．It is indicated that the contribution of the interaction between atoms to the Hamiltonian in the literature is irrational，so the Hamiltonian operator is improved and the squeezing properties of atomic laser coupled output from the system of V-type three-level atomic Bose-Einstein condensation interacting with two-mode squeezed coherent light field are studied．The results show that the interaction intensity of light-atoms in the Bose-Eimtein condenation has evident influence on the fluctuations of two quadrature components of the atomic laser．

Bose-Einstein condensation，V-type three-level atom，squeezed coherent state，squeezed atomic laser

*教育部科学技术研究重点项目基金(批准号:209094)和广西自然科学基金(批准号:2010 GXNSFB013050)资助的课题．

E-mail:liming@glite．edu．cn