关于运用随机前沿法（SFA）研究银行效率的探讨

张 玲，柯 军

（1.蚌埠医学院 社科部，安徽 蚌埠233030；2.上海理工大学 管理学院，上海200093）

关于运用随机前沿法（SFA）研究银行效率的探讨

张 玲1，柯 军2

（1.蚌埠医学院 社科部，安徽 蚌埠233030；2.上海理工大学 管理学院，上海200093）

国内外很多学者运用随机前沿法对银行效率进行了研究。从参数估计、前沿效率函数形式和无效率项分布等三个方面进行了分析，认为其在方法上存在一些不足之处，可能会歪曲银行间效率的比较结果，主张在对银行效率进行研究时应慎用随机前沿法。

银行效率；随机前沿法；存在问题

银行效率体现了银行的综合竞争能力，可以综合地反映银行的业绩。国内外对银行效率进行了大量的研究。国外经历了两个阶段：20世纪90年代以前主要从规模经济和范围经济的角度来衡量商业银行的效率；20世纪90年代以后主要研究商业银行的前沿效率（主要包括X效率、成本效率和利润效率）［1］。我国学者也分别从规模经济和范围经济以及X－效率等方面对我国银行业的效率进行了卓有成效的研究。但笔者认为某些方法在运用上有值得注意的地方。Berger and Humphrey（1997）对有关金融机构效率的研究进行了综述，把最佳业务边界的确定方法分为两大类——参数方法和非参数方法，并指出参数方法的主要缺陷是对最佳效率边界首先假定了函数形式，因而可能导致效率计算出现偏差［2］。对此笔者表示赞同，本文以随机前沿法为例来深入探讨参数估计方法中存在的问题。

一、随机前沿法介绍

我国许多学者运用随机前沿法来研究我国商业银行效率，随机前沿法（stochastic frontier approach－SFA）是一种应用最广泛的研究效率的参数估计方法。其特点是在研究银行效率时定义了效率前沿的函数形式，引进了复合误差项，即成本函数或利润函数受到来自低效率值和随机误差项的共同影响［3］。以利润效率为例，多数学者的研究将商业银行利润函数设定为如下的对数形式：

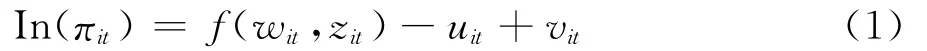
其中πit为第i个银行第t年的利润，wit为相应的投入品和产出品价格向量，zit代表相应的投入和产出要素向量，uit为相应的无效率项，其分布形式有多种假设；vit为相应的随机误差项，服从N（0，σ2ε）分布，uit与vit相互独立，并假设εit＝vit－uit，利润效率的计算公式一般为：

其中g代表（1）式中的参数估计值。X－利润效率的表达式与此相似，只不过将（2）式分母变为E（πit｜－uit＝（－uit）max，g）。

模型将函数f（wit，zit）假定为不存在效率损失的利润函数形式（以下简称理论利润函数）。这一点也可以从uit的假定中看出，uit为无效率项，表示实际利润对理论利润的一种偏离，也即对（1）式中f（wit，zit）值的偏离。

二、模型分析

（一）关于随机前沿法的参数估计方法

1、极大似然估计法（ML法）相对于最小二乘法（OLS法）更适合于随机前沿法的参数估计

有学者在研究中，运用普通最小二乘法进行参数的估计，并对线性回归结果进行了显著性检验，得出利润效率模型线性回归具有较高的样本决定系数，方程也通过了高显著水平的F值检验［4］。有学者分别运用了OLS法和最大似然函数估计法对样本期为2000－2002年的13家商业银行数据进行估计，均得出模型的无效率项（uit）可以在较大程度上解释随机误差项［5］。笔者认为不宜用OLS法进行估计。

正如有学者指出的，OLS法只能根据给定的自变量进行估计，不能综合考虑测量误差及其它不可控因素的影响［3］。也就是说OLS法并没有考虑误差项中的无效率项。但是无效率项的假定在随机前沿法中占有重要位置。另外，从随机前沿法的假定可以看出，εit＝vit－uit项有其一定的分布形式，刘玲玲等（2006）给出了在uit服从半正态分布，vit服从N（0，σ2v）分布且uit与vit相互独立条件下εit的分布密度函数形式［6］。显然E（εit｜wit，zit）≠0（这一结论也适用于uit的其他分布形式），从而不符合误差项条件期望零均值假定，用OLS法参数估计值是有偏的［7］（P79－81）。劳伦斯·克莱因（2000）指出当估计有偏时，系数的微小误差可能导致最终解的巨大误差，并给出了例证［8］（P51－53）。因 此 随 机 前沿法运用OLS法进行参数估计是不合适的，ML法成为其优先选择。

2、ML法需要样本容量足够大

极大似然估计法的优良性质主要体现在大样本的场合，在小样本下却没有一个定理能说明其有什么优良性质［10］（P125－126），因此运用这一方法需要样本容量足够大。这也是大多学者在研究时采用一定时期内我国所有商业银行为样本的一个重要原因，因为这样扩大了样本的容量。

3、在ML法下，（1）式的参数估计结果与uit的分布形式有着极大的相关性

极大似然估计法的参数估计结果依赖于误差项的概率分布形式，在本文中也就是εit＝vit－uit的概率分布形式。如果误差项的概率分布形式未知则无法进行极大似然估计。由于随机误差项vit的分布形式大家意见较为统一，即均值为零的正态分布，那么εit的分布形式就较大程度上取决于uit的分布形式，从而uit分布形式的不同会导致（1）式参数估计结果的不同，进而影响到效率的计算结果。

（二）关于模型中f（wit，zit）形式的设定

1、随机前沿法没有对f（wit，zit）的设定形式加以限制

就（1）式中因变量πit与自变量wit和zit的总体回归模型而言，对于一组被解释变量样本观测值，只能有一种客观的数据生成过程，所以说正确的模型只有一个［11］。而随机前沿法的建模目标并不是寻求πit与（wit，zit）总体上的最佳计量模型关系，它所讨论的是实际利润对理论利润的一种偏离，从而得到效率结果。因此它并不需要找到πit与（wit，zit）总体上的最佳计量模型关系，它只需建立一个理论利润函数形式，并将实际利润与理论利润加以比较即可。

因此，理论利润函数更确切地说应是一个标准，其意义在于提供了一个可资比较的依据，即实际利润与这一标准相差多还是少，从而反应银行效率的低还是高。至于理论利润函数形式孰优孰劣，随机前沿法没有从理论上提出一个判断标准，在银行效率研究的实践中也没有形成一致的最优形式。因此目前理论利润函数形式有不同的设定，如有的学者就将f（wit，zit）设为柯布－道格拉斯函数形式，有的则将其设为超越对数函数形式，有的则将超越对数函数形式中加入时间趋势项等。

2、不同的f（wit，zit）的设定形式会导致效率结果的不同

理论利润函数形式不同必然会出现不同的理论利润。同一（wit，zit）组合在不同的f（wit，zit）形式下，（2）式中的－uit项的具体值会随着f（wit，zit）形式不同而出现变化，从而其利润效率值会发生变化。同样相关研究银行效率的文献也没有阐明随着理论利润函数形式的不同，两个银行的－uit值的大小从而利润效率值在多大程度上会保持一致。如果会出现不一致，那么两个银行的利润效率比较就成为问题。

（三）关于模型中uit分布形式的设定

uit的分布形式有多种假设，如有的学者用此方法研究中国银行业效率时将uit设为服从截尾（在0点处截断）正态分布N（mit，σ2u）［12］，有的则将uit分布形式设为服从半正态（halfnormal）分布，即uit～｜N（0，σ2u）｜。之所以作这样的假定是因为：非效率项不可能降低成本，因而假定为服从被截取的分布［13］［14］。此外uit还有其他分布形式的假定，如指数分布和γ分布等，随机前沿模型相应地可以分为正态－截断正态前沿模型、正态—半正态前沿模型、正态—指数模型、正态－γ分布模型等［15］。研究银行效率的相关文献中并没有对不同的假定提出孰优孰劣的判断标准。由上文可知，uit分布形式的不同假定，势必对（1）式中参数估计的结果产生影响，进而导致效率值发生变化。

有学者提到Berger和Mester（1997）研究发现：选择不同的uit分布假定测得的银行业平均效率值差别不大，也并不显著改变按效率得分对各银行的排序［15］。笔者认为Berger和Mester（1997）的结论本身有两方面问题：（一）结论本身已经表明uit不同的分布是对效率得分有影响的，并且已经改变部分银行排序；（二）至于说影响并不显著，笔者认为这是某一特定条件下的实证结果并不能消除随机前沿法方法上的不足，即它并没有指出uit分布的不同假定在什么样的情况下对银行效率值影响不大，并在多大程度上能够保持两个银行效率值的大小在变化前后保持排序上的一致。如果这一点未得到解决，那么在将随机前沿理论用于研究其他国家银行效率时上述结论就未必成立。

三、结论

通过以上分析，笔者认为：

（一）随机前沿法得出的效率结果如果用于研究银行效率的时间变化趋势从而反映长期变化规律，笔者认为有其合理性，因为有着统一的比较标准。国内许多学者在研究我国商业银行利润效率发展趋势时使用了随机前沿法，研究结果得到了很好的印证和解释。例如，齐树天等用此方法在研究我国商业银行效率演进趋势时得出，在利润效率方面，在1994－2006年样本期内股份制银行和国有银行的利润效率均整体上保持增势［16］。

（二）随机前沿法计算出的效率值可靠性不足，进行银行间效率比较就需要非常慎重。因为该方法运用于银行效率研究时缺乏一个判断f（wit，zit）形式和uit分布形式优劣的标准。f（wit，zit）的形式和uit分布形式不同，效率值也不相同，很可能造成不一致。因此需要一个标准以判断其优劣，那么就可以解决两者设定形式上的不确定性问题。这一标准可以从银行业自身的情况出发来加以研究，也可以在随机前沿法理论层面上来研究。

如果不同银行间的样本数据特征相差较大，这种不确定性也许并不足以掩盖银行间的效率差异，但如果样本数据特征相差不大，那么这种不确定性就很可能会掩盖银行间的效率差异，进而影响其排序。这一点可以在实证分析中看出。以几个研究结果为例，它们均得出国有商业银行比股份制商业银行利润效率低，但并没有提及两类银行内部之间的比较。本文对研究中四个国有商业银行的效率值进行整理排序，结果如表 1 所 示［5］［12］［16］。 分别代表三个研究结果①。从表1中可以看出三个研究结果的排序基本上不一致，且差别很大，其他年份也大致如此，样本期内平均排序也非常不一致。

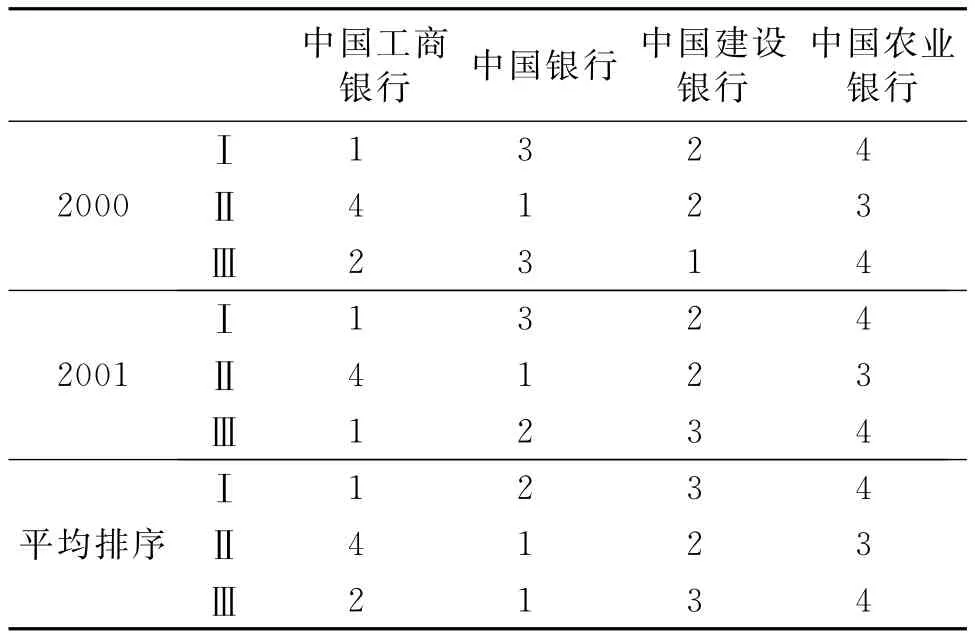
表1 国有商业银行效率排序比较

（三）可靠性不足的另一个来源在于，即便是在同一个f（wit，zit）形式和uit分布形式下，随机前沿法没有说明：一定时期内以我国所有商业银行为样本进行参数估计从而计算出各银行的效率值，与国有商业银行和股份制商业银行分别为样本进行参数估计得出的效率值孰优孰劣，或者从统计上讲在多大程度上能保持排序上的一致性。目前国内此类研究并没有涉及这一问题，大多是用我国全部商业银行为样本进行参数估计。毕竟两类银行的基本情况并不相同，表现在资本实力、规模、管理水平、风险要求、人力资源素质、政策因素、历史因素等各方面的不同，必然有着不同的投入产出结构。一般的计量模型中这种情况是要加以考虑的。因此笔者认为应慎用随机前沿法来研究银行业效率问题。

注释：

①之所以选择这三个研究结果是由于研究中均采用的是随机前沿法计算利润效率，估计方法均为极大似然估计，但在理论利润函数形式和无效率项分布形式上有所不同。

［1］齐天翔，杨大强.商业银行效率研究的理论综述［J］.财经科学，2008，（8）：26－34.

［2］Berger，A.n.，Humphrey，D.B.“Efficiency of Financial Institutions：International Survey and Directions for Research European”［J］.Journal of Operational Reseach，1997，98（2）：175－212.

［3］王聪，谭政勋.我国商业银行效率结构研究［J］.经济研究，2007，（7）：110－113.

［4］李俊玲，陆军，周天芸.中国商业银行X－效率的研究［J］.南方金融，2006，（12）：20－23.

［5］张超，顾锋，邸强.基于随机前沿方法的商业银行利润效率测试［J］.哈尔滨商业大学学报，2005，（4）：525－528.

［6］刘玲玲，李西新.中国商业银行成本效率的实证分析［J］.清华大学学报（自然科学版），2006，（9）：1611－1614.

［7］J.M.伍德里奇.计量经济学导论——现代观点［M］.北京：中国人民大学出版社，2003.

［8］（美）劳伦斯·克莱因.经济理论与经济计量学［M］.沈利生，等，译.北京：首都经济贸易大学出版社，2000.

［9］Battese，G.E.and Collie，T.J.“A Model for Technical Inefficiency Effects in a Stochastic Frontier Production Function for Panel Data”，Empirical Economics［J］.Empirical E－conomics，1995，20（2）：325－332.

［10］茆诗松，王静龙，濮晓龙.高等数理统计［M］.北京：高等教育出版社，2004.

［11］李子奈.计量经济学应用研究的总体回归模型设定［J］.经济研究，2008，（8）：136－143.

［12］姚树洁，冯根福，姜春霞.中国银行业效率的实证分析［J］.经济研究，2004，（8）：4－15.

［13］刘琛，宋蔚兰.基于SFA的中国商业银行效率研究［J］.金融研究，2004，（6）：138－142.

［14］黄隽.中国银行业稳定、效率及其关系研究［J］.中国人民大学学报，2008，（4）：82－88.

［15］王聪，邹朋飞.基于资本结构和风险考虑的中国商业银行X—效率研究［J］.管理世界，2006，（11）：6－12.

［16］齐树天，边卫红，韦艳华.商业银行效率演进趋势及结构特征透析［J］.中央财经大学学报，2008，（8）：23－29.

A Probe into Bank’s Efficiency by Stochastic Frontier Approach

ZHANG Ling1，KE Jun2
（（1.DepartmentofSocialSciences，BengbuMedicalCollege，Bengbu233030，China；2.SchoolofManagement，ShanghaiUniversityofScienceandTechnology，Shanghai200093，China）

SFA has been applied to research the efficiency of banks by many scholars.It has some drawbacks that should influence the reliability of the result of efficiency and retort the comparison of the result according to the analysis which is made from three aspects of the approach in this paper.Therefore，prudence is necessary if SFA should be used to research the efficiency of banks.

efficiency；SFA；drawbacks

F831

A

1009－9735（2011）01－0088－04

2011－01－07

张玲（1978－），女，安徽明光人，蚌埠医学院社科部硕士，研究方向：国际经济法学；柯军（1976－），男，安徽明光人，上海理工大学博士生，研究方向：金融管理。