模糊判断矩阵最优化排序方法研究综述
和媛媛,巩在武
(南京信息工程大学经济管理学院,南京210044)
模糊判断矩阵最优化排序方法研究综述
和媛媛,巩在武
(南京信息工程大学经济管理学院,南京210044)
文章研究基于模糊判断矩阵的方案排序问题。根据完全一致性模糊判断矩阵的特性,依据不同的优化标准建立几种求解排序向量的最优化模型,从而解决具有满意一致性的模糊判断矩阵的方案排序问题,并对常用最优化排序方法进行了总结,初步分析了各种方法排序结果的合理性。
模糊判断矩阵;一致性;最优化模型;方案排序
近年来,许多学者针对模糊判断矩阵排序问题进行了大量的研究。文献[1]从最优化角度提出了模糊判断矩阵排序的权的最小平方法,并给出了严格的理论证明。同时,基于转换矩阵提出了模糊判断矩阵排序的特征向量法,给出了其相应的迭代算法及互补判断矩阵的一致性检验方法。文献[2]针对Fuzzy偏好关系建立了最优化模型,并通过求解该模型得到方案的参考排序值,使得最终方案的排序结果最大程度地反映决策者的偏好。文献[3]利用正互反判断矩阵与模糊判断矩阵的转换关系,探讨了模糊判断矩阵的两种排序方法——对数最小二乘法和对数最小一乘法。在上述研究工作的基础上,本文针对基于模糊判断矩阵的方案排序问题,建立几种求解排序向量的最优化模型,并对常用最优化排序方法进行归纳总结和分析,致力于为决策者选择合理的方案决策方法提供理论依据。
1 相关概念
考虑一个有限的决策方案集(或指标集)X={xi|i=1,2,…,n},记N={1,2,…,n},其中xi(i∈N)表示第i个决策方案。在对方案进行排序时,决策者针对方案集X提供的偏好信息是由一类用实数值表示的模糊判断矩阵给出的。下面给出模糊判断矩阵及其一致性的一些描述。
定义1[4]称直积X'X上的一个模糊子集P∶X×X→[0,1]或为X中的(二元)模糊关系。记pij=μp(xi,xj),pij表示方案xi优于方案xj的相对重要程度,具体规定如下:
(1)pij=0.5,表示xi与xj同样重要;
(2)0≤pij≤0.5,表示xj比xi重要,且pij越小,xj比xi越重要;
(3)0.5 定义2[4]设二元对比矩阵P=(pij)n×n,若满足下列性质: (1)Pii=0.5,∀i∈N; (2)pij+pji=1,∀i,j∈N,i≠j. 则称矩阵P为模糊判断矩阵。其中,性质(2)表示矩阵P具有互补性。 文献[1]给出了模糊判断矩阵的完全一致性定义。 定义4[1]对于模糊判断矩阵P=(pij)n×n,若∀i,j,k∈N,i≠j≠k.有pikpkjpji=pkipjkpij,则称判断矩阵P具有完全一致性。 设A=(aij)n×n为互反判断矩阵,P=(pij)n×n为模糊(互补)判断矩阵,则通过转换公式可得互反判断矩阵A=(aij)n×n。若P=(pij)n×n为完全一致性模糊判断矩阵,则通过公式转换得到的互反判断矩阵A=(aij)n×n亦是完全一致性判断矩阵。对于(完全一致性)互反判断矩阵A=(aij)n×n,则通过转换公式[1]可得(完全一致性)互补判断矩阵P=(pij)n×n。 设ω=(ω1,ω2,…,ωn)T是互反判断矩阵A=(aij)n×n的排序向量,其中当A为完全一致性互反判断矩阵时,则有由转换公式,有pij=,i,j∈N,则P是完全一致性模糊判断矩阵。根据完全一致性模糊判断矩阵的特性,有 据此可导出如下几个等式成立: 若P是非一致性判断矩阵,则上述等式均不成立。为了求解方案的排序向量,根据不同的优化标准,给出以下几种最优化排序方法: (1)权的最小平方法(WLSM) 当判断矩阵P不具有完全一致性,式(2)的等号不成立,则希望求得的排序向量ω=(ω1,ω2,…,ωn)T能够使ωi尽量逼近于,从而构造下列最优化模型: 利用Lagrange乘子法解上述有约束的纯量优化问题[5],得到优化模型的解为 ω=Q-1e/eTQ-1e 其中,e=(1,1,…,1)T, 根据矩阵理论,类似于文献[6]的证明,可证得Q是正定矩阵,且Q-1非负,故有ω>0。 (2)最小二乘法(LSM) 上述模型是非线性最小二乘问题,文献[7]给出了求解该优化模型的简洁的收敛迭代算法。 (3)对数最小二乘法(LLSM) 根据文献[8]求解互反判断矩阵的对数最小二乘优化模型的方法,同理可解得上述优化模型的解为 (4)几何最小二乘法(GLSM) 基于文献[9]提出的几何最小二乘的思想,考虑式(2)的几何意义,希望找到某点ω使得ω至式(2)所示平面方程的平方距离和最短,为此构建以下模型: 其中 (5)χ2方法(CSM) 文献[10]在偏差函数中引入了数量统计中χ2拟合的优化准则,提出了互反判断矩阵的χ2排序方法。根据χ2排序方法的基本原理,在偏差函数中引入χ2拟合的优化准则,构造下列优化模型: 文献[11]给出了求解该最优化模型的收敛性迭代算法。 (6)扩展最小二乘法(ELSM) 文献[12]给出了求解判断矩阵的扩展最小二乘方法的收敛性迭代算法,同理上述模型亦可用该文献给出的迭代算法求解排序向量。 (7)最小偏差法(LDM) 基于式(5),依据文献给出的互反判断矩阵最小偏差法,构造下列优化模型: 文献[13]证明了最小偏差法优化模型的极小值的存在性与唯一性,并提出了LDM的收敛性迭代算法。 (8)最小平方几何距离法(LSGM) 根据文献[14]提出的点平面距离法的基本思想,给出下列优化模型: 令B=(bij)n×n,其中 利用文献[14]导出的点平面距离法的排序公式,解上述优化模型可得 ω=(BTB)-1e/eT(BTB)-1e (9)基于Fuzzy偏好关系的排序方法[2](FRM) 文献[2]给出了一个基于Fuzzy偏好关系的方案排序方法,构造了下列带有约束的最优化模型 并利用Lagrange乘子法求得上述模型的解为 其中, (10)互补判断矩阵排序的权的最小平方法[1](CWLSM) 一般地,式(3)中等式不总能成立,为此文献[1]引入偏差项fij=pjiωi-pijωj,i,j∈N,并构造偏差函数 显然,偏差函数越F(ω)小越好,从而构建以下优化模型[1]: 文献[1]通过Lagrange乘子法解得排序向量为 其中, (11)互补判断矩阵的对数最小二乘法[3](CLLSM) 文献[3]依据式(1),引入扰动函数qij,有由拟合的角度考虑,使qij尽量接近于1,利用极小化函数来达到,给出下列优化模型: 解此优化模型得 针对上一节列举出的目前常见的几种模糊判断矩阵最优化排序方法,下面将对上述排序方法进行归纳总结和比较分析。事实上,根据模糊判断矩阵与互反判断矩阵之间的转换公式,虽然转换前后的两种判断矩阵在形式上发生了变化,但任意两个方案之间的优劣关系却没有改变,原有偏好信息的特征被完整地传递到新的判断矩阵中。所以,可将转换公式直接代入互反判断矩阵的最优化模型中,从而得到模型(M1)—(M8)。因此,上述模型的求解方法、一致性检验均与互反判断矩阵是一致的。比如模型(M3)可看作将公式直接代入互反判断矩阵的对数最小二乘法而得到的,而模型(M11)与之相比较可以看出,在对数运算规则下CLLSM与LLSM两种方法是相同的。由此可见,模糊判断矩阵的LLSM方法可以由互反判断矩阵的LLSM法直接代入即可。 另外,比较模型(M9)与(M10),由于模糊判断矩阵P=(pij)n×n的互补性,即pji=1-pij,则有pjiωi-pijωj=ωi-(ωi+ωj)pij,故模型(M10)与模型(M9)是相同的。并且两个模型各自对应的解中矩阵Q2与Q1只相差一个系数,即有Q1=2Q2,所以有因此,FRM与CWLSM两种方法是完全相同的,故可将两种方法统称为CWLSM。 基于上述分析,模糊判断矩阵的最优化排序方法的排序效果及保序性都应与互反判断矩阵相应方法一致。因此,根据文献[15]对各种互反判断矩阵的排序方法的效果的研究、总结,可得出CSM是排序效果最好的一种排序方法,且排序效果较好的排序算法有LSM、LLSM、LDM,而排序效果比较差的排序算法有WLSM、GLSM以及CWLSM。除此之外,对排序方法的比较还应考虑算法的保序性。Saaty T L指出,当判断矩阵不完全一致时,保序性是决定排序方法优劣的重要准则[16]。根据文献[17]对各种判断矩阵最优化排序方法的保序性的理论分析,可以得到CSM、ELSM、LSGM具有良好的保序性。综上所述,χ2方法(CSM)是相对最好的模糊判断矩阵的最优化排序方法。 本文针对模糊判断矩阵的方案排序问题,根据模糊判断矩阵与互反判断矩阵之间的转换公式,将多种互反判断矩阵的最优化排序方法推广至模糊判断矩阵决策领域,并对常用最优化排序方法进行了总结,并初步分析各种方法排序结果的合理性,从而为决策者选择合理的方案决策方法提供了理论依据。显然,由于最优化模型求解算法的复杂性,关于模糊判断矩阵的最优化排序方法的比较分析还有待今后更深入的比较研究。 [1]徐泽水.互补判断矩阵的两种排序方法——权的最小平方法及特征向量法[J].系统工程理论与实践,2002,(7). [2]樊治平,李洪燕.基于Fuzzy偏好关系的一种方案排序方法[J].东北大学学报(自然科学版),1999,20(6). [3]张卫,马晓燕.模糊互补判断矩阵的对数最小二乘法和对数最小一乘法[J].山东农业大学学报(自然科学版),2006,37(2). [4]樊治平,姜艳萍,肖四汉.模糊判断矩阵的一致性及其性质[J].控制与决策,2001,16(1). [5]陈珽.决策分析[M].北京:科学出版社,1987. [6]王应明,傅国伟.关于层次分析法中权的最小平方法的理论证明[J].系统工程理论与实践,1995,(1). [7]王应明.AHP最小二乘排序方法及其算法研究[J].应用数学与计算数学学报,1997,11(1). [8]许树柏.层次分析法原理[M].天津:天津大学出版社,1988. [9]Islei G,Lockett A G.Judgemental Modeling Based on Geometric Least Square[J].European Jouranl of Operational Research,1988,36(1). [10]Jensen R E.Comparisons of Eigenvector,Least Squares,Chi square and Logarithmic Least Squares Methods of Scaling a Reciprocal Matrix[C].Trinity University,Working Paper,1984. [11]王应明,傅国伟.判断矩阵排序的方法[J].管理工程学报,1994,8(1). [12]王应明.一种用于判断矩阵排序的扩展最小二乘方法[J].厦门大学学报,1997,36(2). [13]陈宝谦.层次分析的两种新排序方法[J].系统工程学报,1990,5(2). [14]王应明,傅国伟.判断矩阵排序的点平面距离法[J].管理工程学报,1993,7(4). [15]袁家新.判断矩阵的排序方法比较及其应用研究[D].南京:南京理工大学,2003. [16]Saaty T L,Vargas L G.Inconsistency and Rank Preservation[J].Journal of Mathematical Psychology,1984,28(2). [17]王应明.判断矩阵排序方法综述[J].决策与决策支持系统,1995,5(3). N945.25;O223 A 1002-6487(2011)07-0165-04 国家自然科学基金资助项目(70901043) 和媛媛(1981-),女,山东泰安人,博士,研究方向:决策分析、系统工程。 (责任编辑/浩天)2 最优化排序方法综述
2.1 最优化排序方法


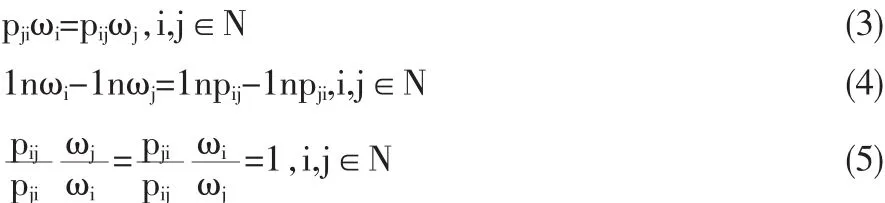
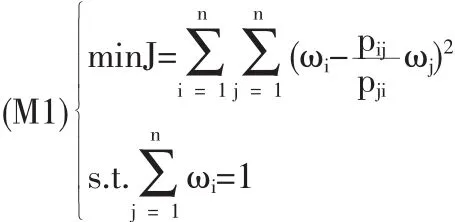













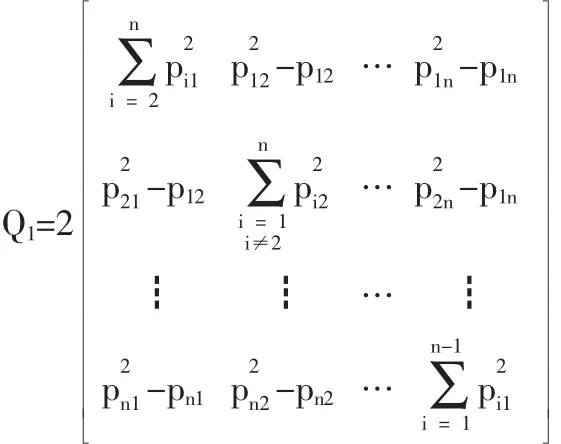

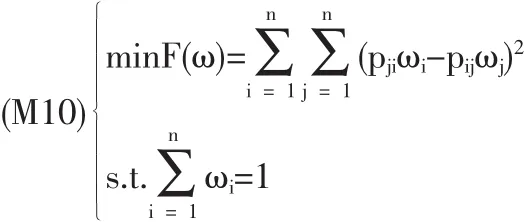




3.2 排序方法比较分析
3 结论

