基于灰色理论的软岩巷道围岩变形预测研究

沈建波,屈建国,詹召伟

(1.山东科技大学资源与环境工程学院,山东青岛 266510;2.济宁矿业集团落陵煤矿,山东邹城 273516;3.济宁矿业集团运河煤矿,山东济宁 272100)

基于灰色理论的软岩巷道围岩变形预测研究

沈建波1,屈建国2,詹召伟3

(1.山东科技大学资源与环境工程学院,山东青岛 266510;2.济宁矿业集团落陵煤矿,山东邹城 273516;3.济宁矿业集团运河煤矿,山东济宁 272100)

在对比不同维数的 G M (1,1)模型和 G M (1,1)等维新信息模型的基础上,得出 G M(1,1)等维新信息模型更适合对软岩巷道围岩变形作预测。在确定了 G M (1,1)等维新信息模型的最佳维数后,对巷道两帮的围岩变形量作了预测,且预测精度较高。

灰色理论;软岩巷道;变形预测;等维新信息模型

变形是煤矿巷道中的普遍现象,软岩巷道围岩变形尤为突出。巷道变形后断面缩小,阻碍运输、通风和行人,因巷道变形而造成巷道报废的现象时有发生,严重影响煤矿安全生产。巷道变形是一个十分复杂的力学问题,在所有影响巷道变形的因素中既有已知因素,也有未知因素,即影响因素的作用特点具有明显的灰色特性,因此,巷道围岩系统是一个介于已知 (白色)和未知 (黑色)系统之间的典型的灰色系统。运用不同的灰色模型预测围岩变形,精度有很大的差别[1-2]。为此,本文通过不同灰色模型的对比,选用 G M (1,1)等维新信息模型对软岩巷道的围岩变形作预测,预测精度较高,为软岩巷道确定合理的支护方案提供了可靠的理论依据。

1 G M (1,1)等维新信息模型的建立

1.1 G M(1,1)模型建立

在灰色预测中,应用最广泛的是邓聚龙教授提出的 G M (1,1)模型[3-4],建模可分 3步完成：

(1)设原始数列 X(0)= (X(0)(1),X(0)(2),…,X(0)(n)),用累加生成法对原始数列进行累加,则一次累加生成的数列为：X(1)= (X(1)(1),X(1)(2),…,X(1)(n)),其中

然后对 X^(1)(t)作累减还原

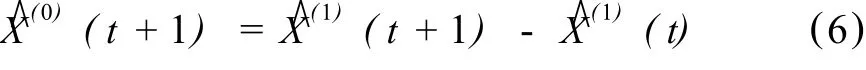
得到了原始数列的模拟值。

1.2 G M(1,1)等维新信息模型建立

G M (1,1)等维新信息模型建模的方法是将G M (1,1)模型的一个值补充到已知数列,同时去掉最老的一个数据,保持数列等维,再建立新的G M(1,1)模型来预测下一个值,并将结果再次补充到原始数列,然后再去掉最老的一个数据,这样依次递补,逐个预测,直到完成预测目标或达到一定精度要求为止。G M (1,1)等维新信息模型有 2个优点：一是及时补充和利用了新的信息,提高了灰区间的白化度;二是每预测 1步模型参数做1次修改,使模型及时得到了改进。正是由于这两个优点,通常都能获得较高的预测精度[5]。本文采用残差大小检验法对模型精度进行检验。原始数据记为 X(0)(t),预测值记为,则相对误差为：

2 软岩巷道围岩变形预测

2.1 软岩巷道围岩变形监测

某矿[6]后组十三轨道上山底板双轨巷道位于松软破碎的变质岩中,由于岩性差、断面大,巷道变形严重,出现喷层开裂、钢筋网弯曲、断面收缩等情况,为此,提出了采用能主动加固围岩强度和施工方便的锚注加固技术,对双轨大断面一段进行加固试验,并对该段试验巷道进行变形预测研究。从掘进工作面向外设 2组测点,1号点距迎头 6m,该段没有采用锚注加固技术,2号点距迎头 11m,该段采用能主动加固围岩强度和施工方便的锚注加固技术,具体监测数据见表 1。

2.2 巷道围岩变形检验性预测

在灰色建模过程中,系统的原始数据不一定都要用来建模,不同维数 (或长度)的序列建模会得到不同的预测结果,而采用选择合适的维数的方法能提高预测的精度。为了建立合适的模型,选取4～7维 1号顶底板位移序列,建立 G M(1,1)模型和 G M (1,1)等维新信息模型,其结果如表 2和表 3。

表1 各测点巷道变形数据

表2 不同维数 G M(1,1)模型顶底板位移预测比较

表3 不同维数 G M(1,1)等维新信息模型顶底板位移预测比较

由表 2和表 3比较可以看出：

(1)G M (1,1)模型预测顶底板位移量,预测的时间越长,误差越大,预测的时间越短,误差越小,因此,G M (1,1)模型不适合对巷道围岩变形做长期预测。这是由于巷道围岩变形从开掘后的破碎变形到围岩进入流变阶段,服从不同的变形规律,在不同的变形阶段用单一的预测公式作长期的预测,这显然是不恰当的。

(2)G M (1,1)等维新信息模型预测顶底板位移量,维数越多 (序列越长)的模型预测误差越大,因此,使用 G M (1,1)等维新信息模型预测顶底板位移量时,不能选的维数过多,否则误差会增大。对于该软岩巷道 4维 G M (1,1)等维新信息模型精度较高,故可选为预测模型,对两帮移近量进行预测。同维的 G M (1,1)模型和 G M(1,1)等维新信息模型相比,G M (1,1)等维新信息模型的误差要比 G M (1,1)模型小的多。这是因为 G M (1,1)等维新信息模型在不断地更新数据时,把新的影响围岩变形的因素加入了预测模型,误差也就变小了。

(3)1号测区第 10天的顶底板位移量已经遗失,根据以上分析,可用 4维 G M (1,1)等维新信息模型对其拟补。经计算得：

2.3 软岩巷道围岩变形预测

对表 1中的两帮位移量建立 4维 G M (1,1)等维新信息模型,预测结果如表 4、图 1所示,通过表 4的相对误差比较可知,预测结果中最大的相对误差是 5.67%,平均相对误差是 4.40%,预测精度较高。

表4 模型预测两帮移近量结果

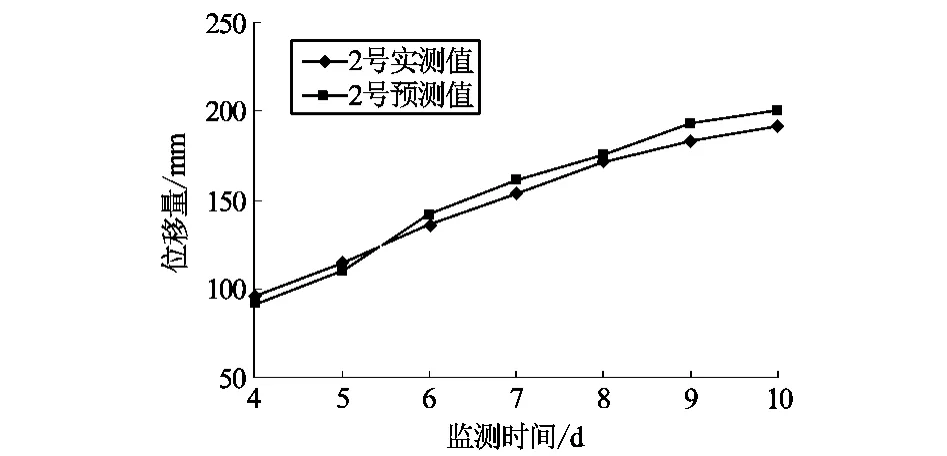
图1 2号测区的巷道两帮变形预测值与实测值比较

3 结论

(1)巷道围岩变形是一个十分复杂的力学问题,可以看作是一个灰色系统问题,G M (1,1)模型预测软岩巷道变形误差较大,且不适合作长期预测。选择合理的维数,使用 G M (1,1)等维新信息模型预测软岩巷道围岩变形量是可行的。

(2)G M (1,1)等维新信息模型不仅采用的数据少,而且不断地将新的数据引入模型,故而考虑了新的影响因素,预测精度较高,能够反映软岩巷道围岩变形的客观发展态势。

(3)G M (1,1)等维新信息模型既可以对巷道围岩变形量作预测,根据预测结果,及时提出合理的支护方案,又可以对矿压监测中缺失的数据进行拟补,具有一定的实用价值。

[1]蒋 刚,林鲁生,刘祖德,等 .边坡变形的灰色预测模型[J].岩土力学,2000,21(3)：244-247.

[2]靳晓光,李晓红,高 茺,等 .隧道围岩位移的灰色优化模型预测 [J].重庆大学学报 (自然科学版),2002,25(1).

[3]邓聚龙 .灰理论基础 [M].武汉：华中科技大学出版社,2002.

[4]吕光华 .矿业灰色系统 [M].北京：煤炭工业出版社,1993.

[5]刘思峰,党耀国,方志耕 .灰色系统理论及其应用 [M].北京：科学出版社,2004.

[6]巩克玉 .灰色系统理论在巷道掘进及围岩变形预测中的应用[D].青岛：山东科技大学,2006.

[责任编辑：李宏艳 ]

Prediction of Surrounding Rock Deformation of Roadway with Soft Rock Based on Grey Theory

SHEN Jian-bo1,QU Jian-guo2,ZHAN Zhao-wei3
(1.Resources&Environment Engineering School,Shandong University of Science&Technology,Qingdao 266510,China;2.Luoling Colliery,Jining Mining Group,Zoucheng 273516,China;3.Yunhe Colliery,Jining Mining Group,Jining 272100,China)

By comparing GM (1,1)with different dimensions and G M (1,1)with geometric-dimension new information,it was believed that geometric-dimension new information model was fitter for deformation prediction of soft-rock roadway.After obtaining the best dimension of G M (1,1)with geometric-dimension new information,the model was used to predict two-side deformation of roadway.The prediction precision was high.

grey theory;soft-rock roadway;deformation prediction;geometric-dimension new information model

TD325.4

A

1006-6225(2011)01-0022-03

2010-09-25

沈建波 (1981-),男,山东邹城人,硕士研究生,从事矿山压力与岩层控制方面的研究。