分散松弛因子在节点电价分解中的应用①

谢云岩， 彭建春， 曾顺意， 曲桂颖， 宋小明

(湖南大学电气与信息工程学院， 长沙 410082)

分散松弛因子在节点电价分解中的应用①

谢云岩， 彭建春， 曾顺意， 曲桂颖， 宋小明

(湖南大学电气与信息工程学院， 长沙 410082)

提出一种分散松弛因子的确定方法。这种方法以当前仍具有有功调节能力的发电机组(边际机组)为对象，先计算边际机组有功出力对负荷有功的灵敏度，再按与灵敏度成正比的方法确定分散松弛因子，继而将这种分散松弛因子应用于电力市场中广泛采用的基于直流最优潮流的节点电价分解模型中，弥补了常规算法无法正确反映边际机组的缺陷。数字仿真结果验证了该方法的有效性。

电力市场； 电价分解； 节点边际电价； 分散松弛因子； 最优潮流

随着电力工业放松管制和电力市场的兴起，节点电价LMP(locational marginal price)理论在国外许多电力市场，特别是北美电力市场中得到了很好的应用[1]。我国华东区域电力市场也在试行节电电价理论框架下的单一买方市场[2]。

LMP定义为满足某节点新增1MW电量需求时的系统边际成本，通常分解为能量电价(energy component)、损耗电价(loss component)和阻塞电价(congestion component)三个分量[5]。系统的能量电价分量主要反映系统的发电成本，全系统的各个节点都具有统一的能量电价；损耗电价分量反映各节点功率对网损的影响；阻塞电价分量反映系统各种安全约束对电价的影响。

较早的文献[6～10]都是基于单个松弛节点的潮流模型确定LMP分量的。由于在潮流分布算出以前，网络中的功率损失是未知的，所以传统潮流问题[11]都要预先指定一个节点作为松弛节点(或称平衡节点)。系统中所有节点的功率增量都是由该松弛节点平衡的，LMP的损耗电价分量也是在该条件下计算的，致使松弛节点的损耗电价分量总为零，松弛节点处的机组没有和其它机组一样平等对待。因此，基于单个松弛节点的节点电价分解模型依赖松弛节点的选取，影响不同市场参与者的经济利益[5]，不利于市场公平、公正的原则。

为了减小潮流计算对单一松弛节点的依赖，文献[12]给出了基于分散松弛节点的潮流计算方法，此后，文献[13～16]对分散松弛潮流做了深入探讨，并将其用于潮流计算、经济调度和电价分解等方面。

分散松弛潮流需要预先给出一组分散松弛因子，该因子的值决定了系统功率失配量的分配方式，直接影响潮流计算结果和电价分解结果。常规分散松弛因子算法是根据各电源的出力比例进行计算的，与各电源出力初始值有关。由此分散松弛因子计算得到的潮流结果和电价分解结果也将与各电源出力初始值有关。

本文首先介绍了基于分散松弛因子的潮流计算方法，分析了分散松弛因子常规计算方法的不足，然后从LMP的定义及分散松弛因子的含义出发，给出了一种基于灵敏度分析的分散松弛因子的确定方法，并将它应用于节点电价的分解计算。

1 分散松弛因子的常规算法

分散松弛因子是在分散松弛(或分散平衡)潮流计算中提出的。为此，下面先给出分散松弛潮流的概念，再说明分散松弛因子的常规算法。

1.1 分散松弛潮流计算模型

基于分散松弛因子的潮流计算首先给出一组分散松弛因子αi，其作用是将有功功率失配量Pm按αi分配到各节点i。有功功率失配量Pm定义为

(1)

式中：N为系统节点集合。

假设系统中共有n个节点，r个PQ节点，G为电源节点的集合，B为线路的集合。基于分散松弛因子的潮流计算方法可用式(2)描述：

(2a)

(2b)

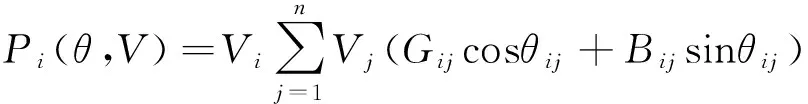
(3)

分散松弛因子αi满足：

(4)

由于式(2b)中未指定各机组的无功出力，所以不需要引入分散松弛因子对无功功率失配量进行分配。式(2a)是对系统所有节点列写的，共有n个等式，式(2b)是对所有PQ节点列写的，共有r个等式，而式(2)共有(n+r)个变量，所以可以仿照潮流计算的牛顿法写出修正方程式：

(5)

式中：H、N、K、L、V-1沿用文献[11]中的定义，矩阵S、T中的元素分别为

(6a)

(6b)

最后，给出各变量初始值，如θ0=0，V0=1.0和Pm=0，就可以用牛顿法求解修正方程式(5)，从而得到潮流结果。迭代过程中，除了对θ、V进行修正外，还要按照式(7)对机组输出功率进行修正。

(7)

1.2 分散松弛因子的常规算法

在计算分散松弛因子潮流时，需事先给出分散松弛因子α的值。

当节点i对应的分散松弛因子αi=1时，表示有功功率失配量Pm仅由单个节点i承担，此时的潮流计算就是传统的使用单个松弛节点的计算，节点i就是该松弛节点。

当节点i对应的分散松弛因子αi=0时，表示节点i不参与有功功率失配量Pm的分配，其输出的有功功率保持不变。

通常，分散松弛因子的值按式(8)确定：

(8)

通过式(7)和式(8)，可以证明每次迭代均满足：

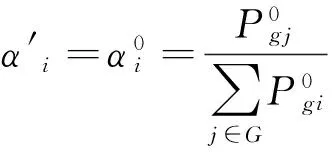
(9)

式(7)表明有功功率失配量Pm按与各电源出力成正比分配。

式(9)说明由式(8)确定的α的值与电源出力的初值有关且在迭代过程中保持不变。

值得注意的是，这种分散松弛因子是人为定义的，它不反映任何电路规律(KCL/KVL)的作用。为此，下面基于电路规律和灵敏度，给出一种新型的分散松弛因子算法。

2 基于灵敏度的分散松弛因子

2.1 基于灵敏度的分散松弛因子算法

求得系统的普通或最优潮流解后(也可以是系统的状态估计潮流解)，将所有出力未达上/下界的机组归为边际机组，所在节点称为边际节点；将出力已达上/下界的机组称为非边际机组，所在节点称为非边际节点。非边际机组的出力认为是不再改变的，所以系统的负荷功率增量将由边际机组平衡。

设负荷节点k的功率增量为ΔPdk，由此带来的损耗增量为ΔPlk，系统总的功率增量就应该为ΔPdk+ΔPlk，根据分散松弛潮流的基本思想，ΔPdk+ΔPlk应由所有分散松弛节点的增出力来平衡，即

Pm=ΔPdk+ΔPlk

(10)

用ηi,k表示电源i出力对负荷k的有功功率的灵敏度，则有

(11)

当负荷节点k的功率增量为ΔPdk时，边际节点i的功率增量为

(12)

(13)

由式(10)和式(13)得：

(14)

当负荷节点k的功率增量为ΔPdk时，为了平衡系统功率，边际节点i的功率增量占所有边际节点功率增量总和的比例(用β表示)为

(15)

本文称边际节点i的功率增量占所有边际节点功率增量总和的比例β为新型松弛因子。由于系统的功率增量是由边际节点平衡的，故非边际节点对应的松弛因子β应该为零。这样就得到了所有节点的分散松弛因子。

2.2 新型分散松弛因子的算法分析

从Pm、β的含义可知，系统功率增量Pm是依据β由所有的边际机组平衡的。从式(11)可以看出，对于不同的节点k，ηi,k的值一般是不同的，从而βi的值也就不同，也就是说，不同节点的功率增量将按不同的比例由所有边际机组平衡，对于不同的节点k，都对应一组βi,k。由式(15)可知，β真实反映了各机组为平衡系统有功功率失配量而新增出力的比例大小。

对于不同的节点k，ηi,k不同，反映了边际机组出力会因负荷节点的不同而不同的事实；同时，分散松弛因子β定义为对系统有功功率失配量进行分配，自然就包括对节点功率增量引起的损耗进行分配，这说明β是与损耗有关的量。当各节点电气位置不同时，节点的功率增量引起的损耗一般不同，所以β也会因负荷节点的不同而不同。

3 新型分散松弛因子在节点电价分解中的应用

3.1 基于直流最优潮流的节点电价模型

本文采用文献[14]给出的直流最优潮流模型计算LMP，该模型可表述为

(16)

(17)

(18)

(19)

(20)

假定节点注入功率为正，线路i-j的潮流方向为i到j，则节点k的电价为

(21)

式中：λ0、μi-j分别是功率平衡式和线路约束不等式对应的影子价格。

(22)

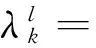
(23)

(24)

3.2 新分散松弛因子在节点电价分解中的应用

将本文提出的松弛因子算法用于节点电价分解，首先应根据松弛因子计算直流模型中的边际损耗因子∂L/∂Pgk和发电机输出功率转移分布因子Di-j,k，然后求解直流最优潮流模型，得到各节点边际电价，最后可根据式(22)～(24)得到分解结果。

需要说明的是，我国华东区域电力市场也在试行节电电价理论，所使用的日前竞价交易出清数学模型[17]与上述节点电价模型相似。但是，由于华东区域电力市场仅开放了发电侧市场，故仅给出发电机组i的上网节点电价。

(25)

用本文提出的松弛因子算法计算损耗因子∂L/∂Pgk和发电机输出功率转移分布因子Di-j,k，然后根据日前竞价交易出清数学模型就可以确定每台机组的中标出力和上网节点电价。文献[3]指出这种处理方法相当于用节点损耗因子对统一结清电价进行修正，以反映其市场效率,与社会效益最大化的目标一致。文献[17]指出上网节点电价λgi可用于对发电企业的日前竞价电量进行结算。因此，将本文方法用于华东区域的电力市场是可行的。

4 算例

本文以PJM5节点系统为例进行分析。为得到阻塞状态，将线路1-2的有功功率潮流约束改为240 MW。各线路参数如图1所示。图1还给出了交流最优潮流解并作为初始潮流解。

首先根据初始潮流解计算边际损耗因子∂L/∂Pgk和发电机输出功率转移分布因子D1-2,k；然后计算灵敏度ηi,k和分散松弛因子β，计算结果示于表1，由于节点4为负荷节点，∀k∈N，η4,k=0，β4,k=0，所以表中略去了η4,k和β4,k值。

当计算得到初始潮流解时的边际损耗因子和转移分布因子后，就可以按照文献[14]中介绍的方法，计算基于分散松弛因子β的边际损耗因子和转移分布因子,然后求解直流最优潮流模型得到潮流结果和各节点电价，最后根据式(22)～(24)给出分解结果，如表2所示。

从表1可以看出，不同节点对应的η、β的值一般是不同的，其中η项准确反映了各节点功率变化引起的各电源出力的微增信息，β项真实反映了各机组为平衡系统有功功率失配量而新增出力的比例大小。

由于各节点的β值不同，根据基于分散松弛节点的节点电价分解算法，它们对应的能量电价也是不同的。

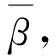
表3同时给出了使用常规分散松弛因子算法计算的β值及节点电价分解结果。

比较两种计算方法，从结果可以看出本文方法计算得到的机组5对应的分散松弛因子为零，这是因为最优潮流分布时机组5为非边际机组，出力不再改变，不能提供额外的功率用于平衡系统的有功功率失配量。而常规计算方法得到的机组5对应的分散松弛因子不为零。所以本文方法可以反映最优潮流分布时边际机组的真实情况。

图1 修改后的PJM5节点系统Fig.1 Modified PJM five-bus system表1 损耗灵敏度因子、转移分布因子和分散松弛因子计算结果Tab.1 Results of loss sensitivity factors，shift distribution factors and participation factors

Bus∂L/∂PgkD1-2,kη1,kη2,kη3,kη5,kβ1,kβ2,kβ3,kβ5,k10.00960.11201.00000.00000.00000.00001.00000.00000.00000.00002-0.0293-0.3685-0.55780.00001.49350.0000-0.59610.00001.59610.00003-0.0473-0.20900.00000.00001.00000.00000.00000.00001.00000.00004-0.0460-0.15090.09180.00000.81970.00000.18960.00000.81040.000050.00000.00000.63800.00000.34520.00000.64890.00000.35110.0000

表2 基于灵敏度分析的分散松弛因子的节点电价分解结果Tab.2 Results of LMP decomposition based on sensitivity analysis

表3 基于常规分散松弛因子算法的节点电价分解结果Tab.3 Results of LMP decomposition using conventional participation factor

5 结语

在基于分散松弛节点的节点电价分解算法中，分散松弛因子起着重要作用。本文根据基于分散松弛节点的节点电价分解法的基本思想，分析了分散松弛因子的含义，并结合LMP的定义给出了基于灵敏度分析的分散松弛因子的确定方法，该方法得到的结果与电源出力初始值无关，通过与分散松弛因子的常规确定方法相比较，可以看出本文给出的确定方法能够反映最优潮流分布时边际机组的真实情况。

[1] 李道强，韩放(Li Daoqiang, Han Fang).美国电力市场中的金融交易模式(Financial transaction modes applied in electricity market in USA)[J].电网技术(Power System Technology)，2008，32(10):16-21.

[2] 周坚，蒋逸静，严正，等(Zhou Jian, Jiang Yijing, Yan Zheng,etal).网损因子法在华东区域电力市场的应用分析(Application analysis of loss factor method in east China power market)[J].电网技术(Power System Technology)，2008，32(3):76-81.

[3] Finney Jhon D, Othman Hisham A, Rutz William L. Evaluation transmission congestion constraints in system planning [J]. IEEE Trans on Power Systems, 1997, 12(3):1143-1150.

[4] Sarkar V, Khaparde S A. Introduction to loss-hedging financial transmission rights [J]. IEEE Trans on Power Systems, 2009, 24(2):621-630.

[5] Cheng X and Overbye T J. An energy reference bus independent LMP decomposition algorithm [J]. IEEE Trans on Power Systems, 2006, 21(3):1041-1049.

[6] Baughman Martin L, Siddiqi Shams N. Real-time pricing of reactive power: theory and study results [J]. IEEE Trans on Power Systems, 1991, 6(2):23-29.

[7] EI-Keib A A, Ma X. Calculating short-run marginal costs of active and reactive power production [J]. IEEE Trans on Power Systems, 1997, 12(2):559-565.

[8] Chen Luonan, Suzuki Hideki, Wachi Tsunehisa,etal.Components of nodal prices for electric power systems [J]. IEEE Trans on Power Systems, 2002, 17(1):41-49.

[9] Xie Kai, Song Yong-hua. Decomposition model and interior point methods for optimal spot pricing of electricity in deregulation environments [J]. IEEE Trans on Power Systems, 2000, 15(1):39-50.

[10]侯芳，吴政球，王良缘(Hou Fang, Wu Zhengqiu, Wang Liangyuan).快速实时电价算法(Fast spot price solution)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2002，14(4):32-35.

[11]何仰赞，温增银.电力系统分析(第三版)[M].武汉:华中科技大学出版社，2002.

[12]Meisel Jerome. System incremental cost calculations using the participation factor load-flow formulation [J]. IEEE Trans on Power Systems, 1993, 8(1):357-363.

[13]River M and Perez-Arriaga I J. Computation and decomposition of spot prices for transmission pricing [C]∥11th PSC Conference, Avignon, France: 1993.

[14]Litvinov Euqene, Zheng Tongxin, Rosenwald Gary,etal. Marginal loss modeling in LMP calculation [J]. IEEE Trans on Power Systems, 2004, 19(2):880-888.

[15]Wu Tong, Alaywan Ziad, Papalexopoulos Alex D. Locational marginal price calculations using the distributed-slack power-flow formulation [J]. IEEE Trans on Power Systems, 2005, 20(2):1188-1190.

[16]Cardell Judith B. Marginal loss pricing for hours with transmission congestion [J]. IEEE Trans on Power Systems, 2007, 22(4):1466-1474.

[17]国家电力监管委员会.华东电力市场运营规则[Z].北京：国家电力监管委员会,2005.

ApplicationofParticipationFactorstoLMPDecomposition

XIE Yun-yan， PENG Jian-chun， ZENG Shun-yi， QU Gui-ying， SONG Xiao-ming

(College of Electrical & Information Engineering, Hunan University,Changsha 410082, China)

A method has been developed to determine the participation factor ,which deals with those so-called marginal generators that still have capability of active power adjustment. Firstly, calculate the sensitivity coefficient of marginal units' active power with respect to load's, then determine the participation factor which proportional to the sensitivity coefficient .The participation factor is applied to the price decomposition model, which is based on Direct Current Optimal Power Flow (DC-OPF) andwidely implemented in electricity market, compensating the conventional algorithms' deficiency that can not correctly reflect the marginal units. The effectiveness of this approach is demonstrated by digital simulation.

electricity markets； decomposition； locational marginal price(LMP)； participation factor； optimal power flow

2010-03-11

2010-04-15

TM731

A

1003-8930(2011)04-0083-06

谢云岩(1984-)，男，硕士研究生，研究方向为电力系统优化运行与控制。Email:xyyhnu@163.com

彭建春(1964-)，男，教授，博士生导师，主要从事电力系统优化运行与控制、电力市场的研究。Email:jcpeng@163.com

曾顺意(1985-)，男，硕士研究生，研究方向为电力系统优化运行与控制。Email:zengshunyi@126.com