考虑不确定因素的逐步倒推法电网规划①

王 淳， 欧阳年会

(南昌大学信息工程学院， 南昌 330031)

考虑不确定因素的逐步倒推法电网规划①

王 淳， 欧阳年会

(南昌大学信息工程学院， 南昌 330031)

针对电力市场环境下输电网络规划面临大量不确定因素的影响，提出考虑不确定因素的逐步倒推法电网规划方法。该方法采用半不变量法计算节点注入功率的各阶半不变量，按直流潮流方程计算状态相量的各阶半不变量，取一阶半不变量为节点状态相量的期望值，二阶半不变量的开二次方为其均方差，并定义待选线路功率的期望值与其投资的二次方之比为其有效性指标。修改的18节点系统和46节点系统验证了该方法的可行性和有效性。该方法计算速度快、且不存在收敛问题，能够用于实际电网规划中。

输电网规划； 不确定因数； 半不变量法； 逐步倒推法

在电力系统的运行和规划中存在多种不确定因素，传统潮流计算的负荷、发电机出力、网络结构和参数都是确定的。对负荷预测或量测的误差、发电和输电元件的随机故障等，若以确定性潮流计算系统的每种可能状态，则计算量巨大且统计分析复杂。开发考虑这些不确定因素的规划和可靠性分析工具符合实际需要[1]。

针对不确定性因素的处理，近年来出现一些新方法。文献[1]用Von Mises提出的方法由各阶矩求离散分布，与正态分布卷积后获得电压和支路功率的分布函数，分析了线路故障对随机潮流结果的影响。文献[2]考虑线路的被选概率，根据电网可靠性要求和算出的被选线路概率，将各待选线路按顺序加入网络，形成一种具有较好适应性的电网灵活规划方案。文献[3，4]分别采用场景决策方法和机会约束规划方法进行不确定规划。文献[5]提出基于蒙特卡罗仿真和遗传算法求解考虑发电和负荷不确定因素的输电网灵活规划，所得方案能兼顾经济性和安全性。文献[6]运用不确定规划理论建立输电网随机期望值规划模型，采用随机数来描述新增发电机节点出力，新增节点负荷变化值，新增线路造价的不确定性因素，利用Monte-Carlo仿真和改进小生境遗传算法求解模型。

本文考虑新增节点的发电机出力及负荷变化，根据半不变量的可加性特点，先分别求出各节点发电机组和负荷功率的各阶半不变量，从而得到各节点注入功率的各阶半不变量，按直流潮流方程计算状态相量θ的各阶半不变量，取一阶半不变量为节点状态相量θ的期望值，二阶半不变量的开二次方为其均方差，结合逐步倒推法对网络进行规划。以修改的18节点和46节点系统进行验证，证明该方法的可行性和有效性。

1 考虑不确定因素的电网启发式逐步倒推规划方法

1.1 不确定的注入功率向量

电力市场的厂网分开，使得输电网的规划模式发生了重大变化，电网投资者的目的从原来的发、输、配电总体利益最大化转变成电网建设和运行利益最大化[5]。在进行输电系统规划时，对未来发电厂址及容量可在相当程度上做出估计。对未来电厂的厂址、容量和负荷等不确定性因素估计后，可用概率密度函数描述这些随机变量并反映到模型中。设规划期内节点i的装机容量 服从离散分布：

(1)

1.2 随机变量的半不变量

对于离散随机变量x取值xi的概率为pi，则随机变量x的期望值为

(2)

各阶中心矩Mv可表示为

(3)

式中v为阶数。

半不变量与中心矩的关系式为

(4)

对于正态分布随机变量N(μ，δ2)，其半不变量求解如式(5)所示。

(5)

半不变量性质1：独立随机变量之和的各阶半不变量等于各随机变量的各阶半不变量之和。

1.3 有效性指标和过负荷检验

采用逐步倒推法考虑不确定因素的输电网络规划，综合考虑待选线路的功率期望值和其投资关系，定义待选线路有效性指标如式(6)所示，即投资小载流期望值高的待选线路为有效线路。

(6)

式中：[Pl]为待选线路l上有功功率的期望值；Cl为待选线路l的建设投资。

过负荷检验采用式(7)所示的关系式。

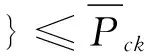
(7)

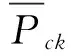
2 考虑不确定因素的电网启发式逐步倒推规划流程

考虑不确定因素的电网启发式逐步倒推规划流程见图1。

1)输入原始数据，包括各节点的负荷和发电出力随机分布、待选线路的各项参数、现有电网结构及参数等。

2)所有待选线路全部加入现有网络，形成虚拟网络，求解网络节点阻抗矩阵X。

3)按随机变量的半不变量计算公式计算节点发电机注入功率和负荷的各阶半不变量，从而得到节点注入功率的各阶半不变量。

4)计算状态相量θ的各阶半不变量，取一阶半不变量为节点状态相量θ的期望值，二阶半不变量的开二次方为其均方差。

5)根据直流潮流模型，计算线路潮流得到线路功率的期望值和方差。

6)按式(6)计算各待选线路有效性指标El，并按从小到大顺序排列(l=1，2，3，…)。

7)去掉线路l后，修正节点状态相量θ的各阶半不变量，重新计算潮流。网络若有过负荷或解列，保留线路l；否则，修正节点阻抗矩阵，返回5)。

8)所有线路是否检验完毕，若是，停止；否则l=l+1，返回到7)。

图1 考虑不确定因素的逐步倒推法电网规划流程图Fig.1 Flow chart of successive backward method fornetwork planning considering uncertainty factors

3 算例

3.1 18节点系统

采用修改文献[13]中的18节点系统，假设所有线路走廊都为可增线路走廊且最大可增线路数量为3，节点11、14、16、18为可能出现的新增电源节点，其概率分布函数服从两点分布；节点11、12、13、14、15、16、17、18为新增的负荷，其负荷预测服从正态分布，有关参数见文献[6]。系统中其它参数与文献[13]相同。

采用逐步倒推法及用VB编制程序求得18节点系统规划结果及线路功率的期望值和均方差如表1所示。

采用考虑节点新增发电机组和负荷不确定因素的逐步倒推法所得规划网络需新增线路17条，扩建线路的总长度为1815 km，与文献[13]中的确定性规划结果相比，其线路有所增加，但系统的适应性有了较大的提高，更能满足实际运行需要。

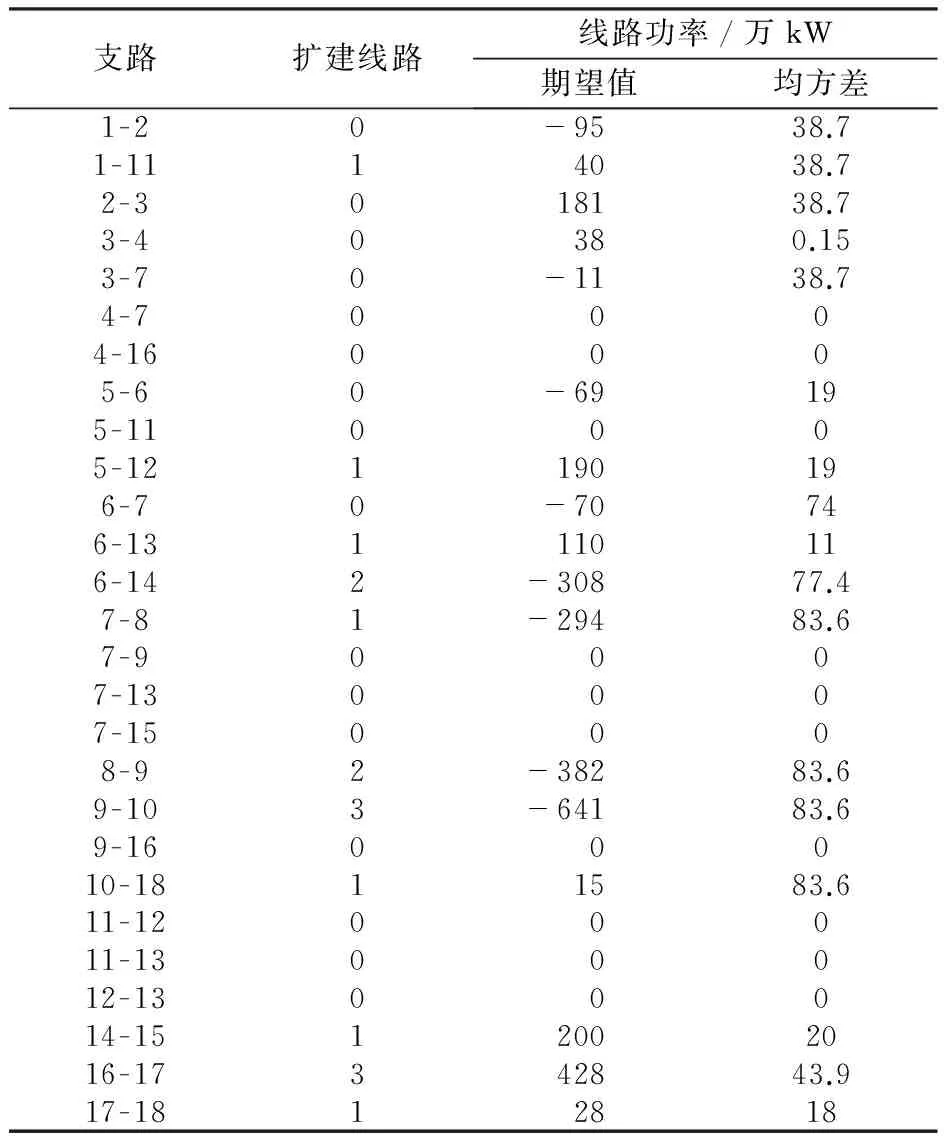
表1 18节点系统规划结果Tab.1 Planning result of 18-bus system planning

3.2 46节点系统

46节点系统的节点和支路数据见文献[15]，假设所有线路走廊都为可增线路走廊且最大可增线路数量为4，节点6、28、31、41 为新增的电源节点；节点3、10、11、15、25、29、30为新增负荷节点且服从正态分布，有关参数见文献[6]。采用本文方法得到46节点系统的规划结果如表2。

表2 46节点规划结果Tab.2 Planning result of 46-bus system planning

本文规划结果与文献[11]确定性规划相比，其扩建线路与投资成本都有所增加，但系统的适应性增强了。

4 结语

针对不确定因素对输电网规划的影响，本文采用半不变量法计算节点注入功率的各阶半不变量，结合启发式逐步倒推法，取待选线路功率的期望值与其投资的二次方之比为有效性指标，对网络进行规划。所得规划方案在未来不确定性环境下更具灵活性和适应性，可在实际电网规划中进一步推广。

[1] 胡泽春，王锡凡，张显，等(Hu Zechun, Wang Xifan, Zhang Xian,etal).考虑线路故障的随机潮流(Probabilistic load flow method considering branch outages)[J].中国电机工程学报(Proceedings of the CSEE)，2005，25(24)：26-31.

[2] 朱海峰，程浩忠，张焰,等(Zhu Haifeng, Cheng Haozhong, Zhang Yan,etal).考虑线路被选概率的电网灵活规划方法(A novel method of electric power network flexible planning considering the selected probability of transmission line)[J].电力系统自动化(Automation of Electric Power Systems)，2000，24(17)：20-24.

[3] 高赐威，程浩忠，王旭(Gao Ciwei, Cheng Haozhong, Wang Xu).考虑场景发生概率的柔性约束电网规划模型(Electric power network flexible planning model based on the probability of scene occurrence)[J].中国电机工程学报(Proceedings of the CSEE)，2004，24(11)：34-38.

[4] 杨宁，文福拴(Yang Ning, Wen Fushuan).基于机会约束规划的输电系统规划方法(Transmission system expansion planning based on chance constrained programming)[J].电力系统自动化(Automation of Electric Power Systems)，2004，28(14)：23-27.

[5] 麻常辉，杨永军，鄢安河，等(Ma Changhui, Yang Yongjun, Yan Anhe,etal).考虑发电和负荷不确定因素的输电网灵活规划(On transmission flexible planning considering the uncertainties of generation and load)[J].电力系统保护与控制(Power System Protection and Control)，2008，36 (21)：29-32.

[6] 范宏，程浩忠，叶幼君(Fan Hong, Cheng Haozhong, Ye Youjun). 基于随机期望值规划的输电网规划方法(Transmission expansion planning based on stochastic expected value programming models)[J].华东电力(East China Electric Power)，2007，35 (12)：16-21.

[7] 武鹏，程浩忠，邢洁，等(Wu Peng, Cheng Haozhong, Xing Jie,etal).不确定信息下的输电网规划新模型(A new transmission network planning model considering uncertain information)[J].电力系统自动化(Automation of Electric Power Systems)，2008，32(13)：21-25.

[8] 麻常辉，薛禹胜，鲁庭瑞，等(Ma Changhui, Xue Yusheng, Lu Tingrui,etal).输电规划方法的评述(A review of transmission planning method)[J].电力系统自动化(Automation of Electric Power Systems)，2006，30(12)：97-101.

[9] 麻常辉，梁军，杨永军，等(Ma Changhui, Liang Jun, Yang Yongjun,etal).基于蒙特卡罗模拟法的输电网灵活规划(Monte Carlo simulation based flexible planning of power transmission network)[J].电网技术(Power System Technology)，2009，33(4)：99-102.

[10]李雪，李渝曾，李海英(Li Xue, Li Yuzeng, Li Haiying). 几种概率潮流算法的比较与分析(Comparison and analysis of several probabilistic power flow algorithms)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2009，21(3)：12-17.

[11]金义雄，程浩忠，严健勇，等(Jin Yixiong , Cheng Haozhong , Yan Jianyong,etal).改进粒子群算法及其在输电网规划中的应用(Improved particle swarm optimization method and its application in power transmission network planning)[J].中国电机工程学报(Proceedings of the CSEE)， 2005，25(4)：46-50，70.

[12]余晓丹，曹树存，那广宇，等(Yu Xiaodan, Cao Shucun, Na Guangyu,etal).基于小扰动稳定域的电力系统概率安全分析(Power system probabilistic security analysis based on small signal stability region)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA) ，2007，19(2)：15-20.

[13]王锡凡. 电力系统优化规划[M].北京：水利电力出版社，1990.

[14]程浩忠，张焰，严正，等.电力系统规划[M].北京：中国电力出版社，2008.

[15]Haffner S, Monticelli A, Garcia A,etal.Branch and bound algorithm for transmission system expansion planning using a transportation model[J].IEE Proceedings: Generation, Transmission and Distribution, 2000, 147 (3): 149-156.

SuccessiveBackwardMethodforNetworkPlanningConsideringUncertaintyFactors

WANG Chun， OU YANG Nian-hui

(School of Information Engineering, Nanchang University, Nanchang 330031, China)

Because of the uncertain factors in electricity market environment,a successive backward method for network planning consdering uncertainty factors is proposed.The cumulant method is to calculate all order cumulants of nodal injection powers and the D.C. load flow equations is to calculate state vector's all order cumulants.The first-order cumulants are taken as nodal state vector's expected values and the second-order cumulants are taken as nodal state vector's standard deviations,and the ratio of the expected value of active power of the elected line to the square of its investment is defined as the effectiveness indicators.The method is proved to be feasible and effective through the modified 18-bus system and the 46-bus system.The proposed method has high calculation speed,and does not hare convergence problems,so it can be used in practical network planning.

transmission network； uncertainty factors； the cumulant method； successive backward method

2009-09-08

2009-11-23

TM715

A

1003-8930(2011)02-0050-04

王 淳(1963-)，男，博士，副教授，研究方向为电力系统规划及可靠性、优化理论在电力系统中的应用。Email:cwang_ncu@163.com

欧阳年会(1982-)，男，硕士研究生，研究方向为电力系统规划。Email:oynh4833@sina.com