串联电路系统可靠度最大化的算法研究

李帅 杨康

沈阳理工大学信息工程学院

串联电路系统可靠度最大化的算法研究

李帅 杨康

沈阳理工大学信息工程学院

对电子电路系统而言，如何使其获得最大的可靠性是设计的主要目标之一。文章给出了粒子群算法的可靠性优化求解策略，根据数学模型，讨论了求解步骤，还加入变异操作来避免早熟收敛，最后给出了实验仿真结果。结果表明该算法与其他方法相比收敛速度更快，精度更高，从而验证了该算法应用于最大化串联电路系统可靠性问题的可行性和有效性。

可靠性；最大化；单目标优化；PSO算法；变异操作

由于计算机性能的提高和软件技术的发展，使得优化过程得以快速、容易地实现，缩短了可靠性优化设计时间，促进了可靠性优化方法在可靠性设计中更加广泛的发展和应用。以往的最优冗余大多关注于在满足一定的可靠性要求下,整个系统的成本最小,少有关于系统可靠度最大化的研究。

1. 单目标优化模型建立

系统可靠性优化问题按照其目标函数数目的多少分为：单目标优化和多目标优化。单目标优化：是指在一定资源消耗的条件下，优化目标为最大化系统可靠度或者最小化系统资源消耗的单一优化问题，最终获得一个最优解。

在串－并联电路系统中，最大化系统可靠度的问题可用如下优化模型表示:

式中：ni为第i级子系统的冗余数；qi(qi=1-Ri)为第i级子系统各不相同元件的不可靠度；g（ni）为第i级子系统单元成本，Ri为子系统各相同元件的可靠度。

图1 串－并联冗余系统

若qi＜＜1,目标函数还可以表示为

对非线性规划(2),若目标函数f(x)是凸函数,约束集合是凸集,则称非线性规划(2)是凸规划。显然在(2)中只含不等式约束,又gi(x)是凹函数,则约束集是凸集。存在定理:凸规划的局部最优解必是全局最优解.求解问题式(2)就是在可行集中找出一点x*使得目标函数f(x)在该点处取得最小值。

2. PSO算法

系统可靠性优化已被证明是一个NP完全问题，很难采用基于梯度的微分方法求解，即不存在精确的求解方法。为此，本文采用粒子群优化算法(PSO)来进行复杂系统的可靠性优化分析。它是一种现代群体智能算法，1995年首先由Kennedy和Eberhart提出[1],是以所有粒子追随着最优粒子飞行，在解空间中进行随机搜索。每个潜在解与粒子运行速度相联系，该速度不停地根据粒子经验以及粒子邻居们的经验来调整大小、方向，总是希望粒子能朝着更好的方向发展。在搜索过程中，全局搜索能力与局部搜索能力的平衡关系对于算法的成功起着至关重要的作用。粒子更新公式如下所示：

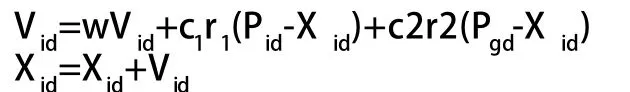
其中w称为惯性权值，c1和c2是两个正常数，称为加速因子，r1和r2是两个0～1之间的随机数.通常使用一个常量Vmax来限制粒子的速度，改善搜索结果。

用粒子群算法求解本文的问题，具体可按如下步骤进行：

首先注意到本文的最优解是在整数空间，即使粒子的位置和速度均为整数，下一位置则可能为实数，这样不能保证仍在整数空间内搜索。本文取变量y1，y2，…均属于[0，1]区间的实数，其值对应于粒子的位置。xi与yi对应，若k=[liyi]，则xi取整数集合｛n1，n2，n3，…,nm｝中的第k个元素，即xi=n1+k-1。这样[0，1]区间的实数就与整数对应起来。目标函数:

另外在有约束的极小化问题的惩罚函数中，适应值函数定义为最小不可靠度模型的目标函数和对违反约束的惩罚之和。有约束的问题“变成无约束的优化问题”即

式中,M为一充分大正数。

设每一个冗余子系统的n值为Xi，则每一个粒子的编码为[X1，X2，…，Xn]，种群大小popsize设置为20，粒子飞行最大速率Vmax=2.0，种群规模为20，最大迭代次数为100,c1=1.4946，c2=1.4946，惯性权重w由0.9～0.4线性减小,M为18。

算法描述：

Stepl初始化所有的粒子，在允许的范围内随机设置粒子的初始位置和初始速度;

Step2判断每个粒子是否满足约束条件;

Step3评价每个粒子的适应值，即计算目标函数值；

Step4计算个体历史最优位置pbest；

Step5计算种群历史最优位置gbest；

Step6根据粒子的速度和位置更新方程更新粒子的速度和位置；

Step7若满足迭代条件，则终止迭代，输出结果；否则转到Step2。

3.求解实例

设某4级串一并联系统，总造价不大于200元，各级别元件不可靠度及单价数据见表1，求最佳冗余设计方案，使系统可靠度最大。

用matlab进行仿真求解,得到如下结果:迭代进化得到的适应度值:0.049.(见图2)。

图2 pso求解的适应度进化曲线

粒子群优化算法收敛快，具有很强的通用性，但同时存在着容易早熟收敛，搜索精度较低，后期迭代效率不高等缺点。在粒子群优化算法中引入变异操作，即对某些变量以一定的概率重新初始化。变异操作拓展了在迭代中不断缩小的种群搜索空间，使粒子能够跳出先前搜索到的最优值位置，在更大的空间中开展搜索，同时保持了种群多样性，提高算法寻找到更优值的可能性(迭代过程见图3)。

表 1

图4 20次平均适应度进化曲线

因此，在普通粒子群算法的基础上引入了简单变异算子，基本思想就是粒子每次更新之后，以一定概率重新初始化粒子，最终得到最优解[3]。

最优解:n1=1,n2=3,n3=1,n4=1,n5=2,n6=1,n7=1,n8=2;此时的系统最大可靠度R=0.9949。没有冗余优化的8级串联系统可靠度为0.400,由此可见，群智能算法对于解决最大化复杂系统可靠性问题具有一定的高效性和易实现性。

为了检验算法的有效性，本文同时采用了遗传算法和模拟退火算法对该问题进行求解。遗传算法参数如下：种群规模为N＝20,交叉概率为pc=0.95,变异概率为pm=0.08,迭代次数为100; 模拟退火算法参数如下：起始温度T=100000，终止温度T0=1,退火速度为0.9。三种算法随机运行20次所找到的平均最小适应度进化曲线所示。显然，粒子群算法的要比其他算法进化的快，而且结果也优于另两种算法（见图4）；通过比较三者的目标函数值的标准方差,发现粒子群算法的方差比其他算法的小一个数量级,说明粒子群算法求最优解时,优化表现比较平稳；另外,粒子群达到最优的频率明显大于其他算法(见表1)。

图3 改进的pso求解的适应度进化曲线

4.结束语

以往解决可靠性优化问题都是从整个系统的成本最小化的角度建立单目标优化模型,本文则从串联电路系统可靠性最大化的角度建立了数学模型。

在粒子群算法求解的过程中注意到本文的解都应该在整数空间,因此对模型进行了改进，并通过加入罚函数的方法将有约束问题转化为无约束问题，最终形成了适合粒子群算法的目标函数。

粒子群算法作为一种全局搜索算法，尤其适用于处理传统搜索方法难以解决的复杂问题和非线性问题，但是它却不能保证最终收敛于问题的全局最优解。在算法中引入变异操作后，通过仿真发现这种自变异的粒子群算法克服了早熟收敛，搜索精度较低，后期迭代效率不高的缺点。

考虑到遗传算法存在早熟的弱点,而模拟退火算法全局搜索能力差，经过改进的粒子群算法能够较好地克服了这两种算法的缺点。通过实际算例仿真计算验证了自变异粒子群算法与遗传算法。模拟退火算法相比在求解串联电路系统可靠度最大化时无论是求解过程还是结果，这种算法都胜过其他两种算法。因此，加入变异操作的粒子群算法为串联电路系统可靠性最大化问题的求解提供了新的思路。

[1]Kennedy J, Eberhart R. Particle swarms optimization [A]. Proc IEEE Int Conf on Neural Networks[C]. Perth, 1995: 1942-1948

[2] Eberhart R C, Shi Y. Particle swarm optimization: developments, applications and resources[A].Proceedings of the IEEE Congress on Evolutionary Computation [C]. Piscataway, NJ:IEEE Service Center, 2001: 81-86

[3]吕振肃，侯志荣.自适应变异的粒子群优化算法.电子学报. Mar.2004, Vol.32 No.3

[4]丰建荣，刘志河，刘正和.混合整数规划问题遗传算法的研究及仿真实现.系统仿真学报.2004，16(4)：845～848

[5]飞思科产品研发中心 编著. MATLAB 6.5辅助优化计算及设计.电子工业出版社

[6][加]B.S.迪隆.系统设计和应用的可靠性工程.宇航出版社

[7]谢云.用模拟退火算法并行求解整数规划问题.高技术通讯.1991，1(10)：21—26

10.3969/j.issn.1001-8972.2011.18.011

辽宁高等教育教学资源平台建设

李帅， 男 沈阳理工大学信息工程学院硕士研究生。 研究方向:虚拟仪器与信息处理。