可靠度理论在隧道衬砌结构设计中的应用
陕西铁路工程职业技术学院 高攀科
可靠度理论在隧道衬砌结构设计中的应用
陕西铁路工程职业技术学院 高攀科
可靠度理论在工程结构设计中的应用从20世纪40年代开始。我国从20世纪50年代开展了极限状态设计方法的研究工作,20世纪50年代中期,采用了前苏联提出的极限状态设计方法。20世纪60年代,土木工程界广泛开展结构安全度的研究与探讨。20世纪70年代开始在建筑结构领域开展可靠度的理论和应用研究工作,并把半经验半概率的方法应用到工业与民用建筑、水利水电工程、港口工程、公路工程和铁路桥梁等6种有关结构设计的规范中。目前,我国以可靠度理论为基础修订铁路隧道设计规范的工作取得了重大进展,并完成了新的《铁路隧道设计规范》(JB10003—99),其机构采用“荷载—结构”模式。
在隧道建设理论中,随着岩石力学的发展和锚喷支护的应用,逐渐形成了以岩石力学理论为理论基础的,支护与围岩共同作用的现代支护结构原理。当前国际上广泛流行的新奥地利隧道设计施工方法,就是基于这一支护原理。本文,笔者简述了用随机有限元对隧道锚喷支护结构进行分析的基本方法和过程,在现场勘察资料还比较欠缺的情况下,按概率及数理统计原理,利用蒙特卡洛法(Monte—Carlo),通过计算机对随机变量取样,然后对某隧道二次模注混凝土衬砌的承载能力极限状态可靠度作了初步评估。
一、蒙特卡洛法简介
当前在工程实践中均采用可靠指标β作为构件或结构可靠度的度量指标:

其中,μZ、σZ为构件的均值和标准方差。
若要得出结构的可靠指标β,首先应求得构件抗力R、荷载效应S的统计特征μR、μS、σR、σS,就必须有大量用于计算的原始几何与物理力学参数,但由于现场地质勘察资料还不充足,为此,采用较为简单且精度较高的Monte—Carlo试验法。Monte—Carlo法对结构工程中不确定性的统计分析,特别是对于那些通过非线性方程来表达数量很多的随机变量之间关系的问题,是一个行之有效的工具。
该方法的基本原理是:首先对各基本随机变量X通过计算机进行随机抽样,分别获得其分位值x1,x2,…,xn。利用随机函数产生(0,1)之间的均匀分布随机数u1,u2;将u1,u2转换为标准正态分布随机数r1,r2;将标准正态随机数r1,r2转换为基本变量实际分布随机数xi。其次,根据所得X的大量样本求出X的统计μx、σx、δx,并用假设检验方法求出X的概率分布。
二、可靠度分析
由于坍方段的覆盖层薄、围岩松散破碎,地表渗水对洞身围岩的稳定性影响大,且洞身中、下部及仰拱开挖支护扰动时会进一步影响其稳定性,故必须对地表坍腔及坍塌体、洞内坍口及相邻初期支护段进行紧急加固处理,防止坍方的进一步扩大。具体实施简述如下。
1.建立分析模型。笔者在对围岩与衬砌结构相互作用机理的处理上采用主动荷载加围岩弹性约束的模型。此模型认为在非均匀分布的主动荷载作用下,衬砌结构的一部分将发生向围岩方向的变形,只要围岩具有一定的刚度,就必然会对衬砌结构产生弹性抗力以抑制它的变形;衬砌的另一部分则背离围岩向着隧道内变形,不产生弹性抗力,形成所谓的脱离区。如图1所示。
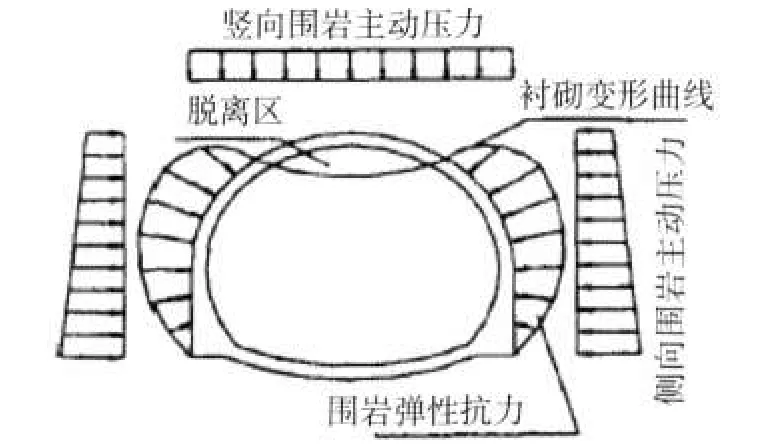
图 1 围岩与衬砌结构相互作用机理模型
2.模型求解。由上述分析可知,衬砌结构的内力分析是个非线性问题,须采用迭代或某些线性化的假定:转换成超静定结构求解。并将它简化成一个平面应变问题。根据结构力学原理,把衬砌结构离散成50个梁柱单元,单元之间采用刚性节点联结,在节点上安设只承受压力的弹性支座,各单元编号顺序如图2所示(根据对称性,图中仅给出半跨的情况)。用矩阵位移法进行求解。
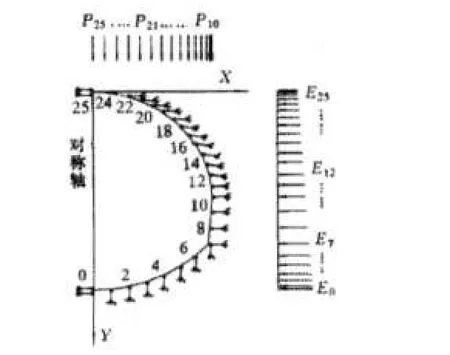
图 2 衬砌单元编号示意
3.利用Monte—Carlo法计算参数。计算时把围岩容重γr侧压力系数λ、垂直荷载高度(或埋深)hq、围岩的弹性抗力系数Kr、衬砌结构的弹性模量Ec、混凝土容重γc、结构的厚度d以及混凝土的抗拉强度fcl与抗压强度fca等几何与物理力学参数均当作随机变量,对以上各参数采用蒙特卡洛法,由此得出衬砌的相关位移与内力的均值和方差,并计算出衬砌结构的可靠指标。
三、工程实例
分析了某隧道衬砌筛选的3种断面:单心圆、坦三心圆和尖三心圆在Ⅴ级围岩(浅埋)荷载作用下,二次模注混凝土衬砌的可靠度进行了计算分析(图3为推荐的单心圆断面形式)围岩与衬砌结构各随机变量统计特征结果见表1(仅列Ⅴ级围岩的统计结果)。从表1中数据可以看出,与围岩荷载有关的计算参数多呈对数正态分布,而与衬砌几何、力学性能有关的指标侧均呈正态分布。而衬砌厚度d的变化范围也大致能反映洞室开挖后内轮廓的凹凸不平。

图 3 隧道内轮廓优化单心圆(cm)

表 1 Ⅴ级围岩与衬砌结构各随机变量统计
为便于分析,将衬砌结构的可靠指标计算结果中几个具有可比性的关键部位,如边墙脚、最大跨度处、限界高度为4m处、拱腰、拱顶以及最小的可靠指标列于表2进行比较。根据《铁路隧道设计规范》衬砌结构截面目标可靠指标β值在承载能力极限状态时取3.7,正常使用极限状态时取1.0。结果表明只有拱顶和边墙局部的值β小于3.7,但都大于1.0。

表 2 Ⅴ级围岩浅埋3种断面主要部位可靠度指标β值
四、结论
通过蒙特卡洛法对该隧道衬砌结构进行了承载能力的可靠度分析,得出了以下一些结论。
1.就整体衬砌结构的力学性能与施工时洞室开挖的稳定性而言,单心圆最佳,尖三心圆次之,坦三心圆最差。
2.在Ⅴ级围岩地段仰拱厚度宜适当增加(≥40cm)。Ⅴ级围岩深埋地段亦应设计仰拱。
3.单心圆衬砌结构大部分截面都能满足承载能力极限状态时的受力要求,虽然还存在局部截面的可靠指标不能达到“理想值”,但不会导致结构整体失效。工程实践证明,只有当衬砌的拱圈或边墙的大部分部位失效时,衬砌结构才会失去承载能力。

