感应电能传输系统多谐振点及其自治振荡稳定性分析*

唐春森 孙 跃 戴 欣 王智慧 苏玉刚 呼爱国

1)(重庆大学自动化学院，重庆 400044)2)(奥克兰大学工程学院，奥克兰 1010，新西兰)(2010年9月1日收到;2010年11月10日收到修改稿)

感应电能传输系统多谐振点及其自治振荡稳定性分析*

唐春森1)孙 跃1)戴 欣1)王智慧1)苏玉刚1)呼爱国2)

1)(重庆大学自动化学院，重庆 400044)2)(奥克兰大学工程学院，奥克兰 1010，新西兰)(2010年9月1日收到;2010年11月10日收到修改稿)

以串联型感应电能传输(IPT)系统为例，用非线性动力学的方法研究了IPT系统的多谐振点的判断及稳定性分析问题.建立了系统的频闪映射模型，根据不动点理论推导出了系统的稳态响应分段解析函数式，并在此基础上，给出了系统谐振工作点的理论判据，结合系统庞加莱映射的雅可比矩阵特征值分布情况，给出了谐振点的稳定性判据.结合具体实例系统，讨论了其多谐振点现象，并通过仿真和实验进行了验证，证明了本文理论分析结果的正确性.本文所提出的分析方法也可为其他类似谐振变换电路的建模及稳态工作点分析提供一定的理论参考.

感应电能传输(IPT)，频闪映射，雅可比矩阵，稳定性

PACS:84.30.Jc，05.45.－a

1.引 言

感应电能传输技术(inductive power transfer，IPT)是一种借助高频电磁场将电能从电源端耦合到负载端的电能传输新技术.由于能量发射(原边)与接收(副边)部分完全绝缘且可以相对移动，使得电能传输过程具有更加安全、可靠及灵活等优点，因此该技术在某些特殊领域具有无可比拟的优势.如用其为生物体内植电装置充电或供电，则可以大大降低手术的风险及病人的痛苦［1，2］;用其为有轨电车供电，则可以彻底去除传统滑动或者滚动取电存在的电磁污染、不安全及不可靠等缺点［3］;在易燃易爆环境、潮湿甚至水下环境用电设备的供电方面，本技术也提供了绿色安全的解决方案［4］.因此，近年来，对该技术的研究已成为电力电子领域的一个热点.

IPT系统的核心环节是电与磁的两次转换，即原边实现由电能到磁能的转换，副边实现磁能到电能的转换.虽然这与变压器功能类似，但是与变压器的紧密耦合特性不同，IPT系统具有典型的松耦合特性，其原副边间的耦合系数通常低于甚至远远低于0.5［5］.为了提高能量转换的效率和功率传输的能力，系统主电路拓扑通常采用原副边均谐振的形式，主要有并联谐振、串联谐振以及串并混联谐振等［6］.然而开关谐振电路的应用，虽然大大提高了系统的功率传输能力，却也使得系统数学模型呈现出典型的高阶非线性特性，从而导致系统存在复杂的动力学行为，最显著的在于多软开关工作点的存在.文献［7］在 LCL型谐振电路中发现了多软开关工作点的存在，并研究了参数变化对软开关工作点的影响以及各工作点上的稳态特性.

谐振工作点是软开关工作点的一种特殊情况，即开关频率与谐振电压及电流的振荡频率一致的软开关工作点.IPT系统主要有定频和浮频控制策略两种常规控制方法［8］.定频模式下，系统开关频率固定，不随参数变化而变化，因此，在负载切换或者参数漂移时，系统很容易进入硬开关工作状态，引起较大的开关损耗和EMI.而浮频模式下，系统开关频率跟踪谐振频率，每次开关谐振电压或者电流过零时切换开关管，可以保证系统总工作在软开关状态，因此浮频模式相对于硬开关模式具有更好的参数自适应能力.然而由于系统的高阶非线性特性，使得系统存在多软开关工作点的同时，还可能存在多谐振工作点，这使得浮频控制模式下的IPT系统具有更为复杂的动态过程.文献［9—12］发现在某些情况下，IPT系统存在频率跳变的现象.文献［11—14］基于阻抗分析方法对系统的频率稳定性问题进行了探讨，但是由于阻抗分析方法的基波近似特性，使得这种方法的分析精度存在一定的限制，在分析系统频率分岔行为方面，甚至可能造成错误的结果［7］.

频闪映射及庞加莱映射方法是分析非线性系统的两种典型离散化方法，广泛应用于DC-DC变换器的分岔及混沌等非线性行为分析及控制方面［15—19］.本文以原副边均串联谐振的感应电能传输系统为研究对象，基于频闪映射方法及不动点理论提出一种周期振荡稳态分析方法，给出一种新的谐振点判据，并结合庞加莱映射方法推导出其自治振荡稳定性判据.结合实例系统，分析了其谐振点分岔现象及各谐振点稳定性，并进行了仿真及实验验证.

2.频闪映射模型及系统稳态响应

感应电能传输系统实质上是一个可分段线性化的高阶开关切换系统，稳态时，系统呈周期振荡状态，各状态变量周期性重复，因此以工作周期为采样时间间隔对系统进行采样，将得到一个稳态不动点.据此，本文首先建立系统的频闪映射模型求取其周期不动点，再以周期不动点为初值，计算各状态变量的稳态响应函数.

图1 串联谐振型IPT系统主电路

图1所示为串联谐振型IPT系统的主电路拓扑，其中开关管S1—S4组成的全桥逆变器将直流电源Edc变换为高频交变电压加到谐振回路上.实际控制中，由于开关管开通和关断过程的延迟，使得桥臂存在短路的风险，因此通常要设置一定的死区时间，以避免引起电源短路.死区时间很小的情况下，逆变器输出电压波形为近似方波，这里为简化分析，将开关管进行了理想化，即开关过程在瞬间完成，且导通损耗为零.

如图1所示的串联谐振型IPT系统，根据前面的理想开关假设，谐振回路的输入电压可以表示为

其中，T为系统稳态开关周期.

分别取系统原副边的谐振电流及谐振电压组成系统状态向量，取谐振回路输入电压为系统输入向量，即 x= ［ip，up，is，us］，u= ［uin］，则根据电路原理可得系统状态空间模型为

式中

(2)式的解析解为

式中Φ(t)=eAt.

半周期内，输入电压是恒定不变的，因此，(3)式可以简化为

设xn(T)与xn+1(T)为第n周期的初始状态及终止状态，则由(4)式可得稳态下系统以周期T为采样时间间隔的频闪映射模型为

因为稳态时系统状态必然周期性重复，即xn+1(T)=xn(T)，则由(5)式的迭代方程可得状态的周期不动点为x*(T)=xn(T)=xn+1(T)，即以此不动点 x*(T)为周期初始值，则稳态周期响应为

3.谐振工作点及其稳定性分析

3.1.谐振工作点及其判断条件

在谐振工作点上，系统工作于软开关状态且开关频率和振荡频率一致.为了便于准确判断一个开关频率是否对应于系统的一个谐振工作点，这里在前面得到的系统状态的周期不动点及稳态响应函数基础上，从系统状态中分离出原边谐振电流分量，根据系统的软开关工作条件及谐振工作点的频率特征，给出谐振工作点的判断条件如下:

式中Y=［1 0 0 0］为状态选择矩阵，用于从系统状态中分离出原边谐振电流分量.

满足(8)式的所有非零解均为系统的谐振周期，每个谐振周期值对应系统的一个谐振工作点.然而由于(6)，(7)式均为超越方程，因此很难推导出(8)式的解析解，通常只能借助于计算机进行数值求解.

3.2.谐振点自治振荡稳定性分析

前面已经推导出了系统稳态谐振点的判断方法，但是这些导出的稳态谐振点能否在浮频模式下稳定存在，还需要对其稳定性进行分析.在浮频控制模式下，IPT系统工作于自治振荡状态，全桥逆变器根据原边谐振电流的方向实时切换，即原边谐振电流ip每次过零时关闭当前导通的一对开关管并打开另一对互补的开关管，则逆变器的输入电压的数学模型可以表示为

在动态过程中，系统各模态的切换取决于状态变量ip的方向，因此各模态的工作时间是不定的，设模态1和2的工作时间分别为ξ1和ξ2，则系统模态切换的边界条件为每次切换时原边谐振电流为零，即

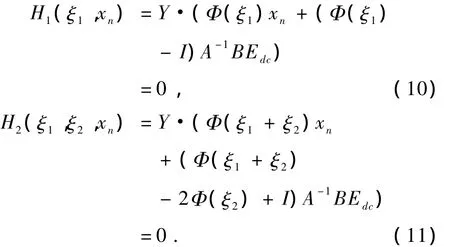
由(10)，(11)式可知，模态持续时间 ξ1和 ξ2均为状态xn的函数.

由(4)式可得系统自治振荡模式下的周期迭代模型(庞加莱映射模型)可表示为

与(5)式所示的频闪映射模型不同的是，上式所示模型中模态持续时间ξ1和ξ2均为状态xn的函数，由(10)和(11)式所示的ZCS软开关边界条件所确定.在稳态下，因为两个线性模态的持续时间相等，分别为半个稳态周期，则(12)和(5)式形式上完全等价.物理意义上，(5)式是针对固定频率的系统周期采样模型，对硬开关和软开关运行模式均适用，而(12)式为系统软开关运行模式下的周期迭代模型，满足条件的相轨迹在稳态时正好周期性地穿过软开关边界条件所确定的庞加莱截面.因此，为了判断(8)式所确定的谐振工作点的自治振荡稳定性，我们可以以周期不动点x*为(12)式所示周期迭代模型的初始状态，在干扰Δx作用下，经历一个周期后，观察此干扰的作用是被抑制还是放大，即是否收敛于初始状态点.这可以通过分析(12)式的雅可比矩阵特征值的分布情况来实现.

定义系统雅可比(Jacobi)算子为

由软开关边界条件方程(10)和(11)式，根据隐函数求导法则，可得

(14)，(15)式代入(13)式可得系统雅可比矩阵为

式中各偏导项的计算可由(10)—(12)式导出

根据Floquet定理［20］可知，如果系统雅可比矩阵的所有特征值λ均位于单位圆内，即模均小于1，则对应谐振工作点的自治振荡是渐近稳定的，若有一个特征值的模大于1，则对应谐振工作点的自治振荡是不稳定的.

4.多谐振点现象研究

这里将对一个串联谐振型IPT系统的多谐振点现象进行研究，利用前面的理论分析结果确定该系统的多个谐振点的工作频率，并分析各工作点的自治振荡稳定性，分析结果通过仿真和实验结果进行了验证.

4.1.多谐振点现象

对图1所示的串联谐振型IPT系统，假设其参数取值如表1所示.

表1 串联谐振型IPT系统参数表

根据(8)式所示谐振工作点判断条件，可以得到系统在表1所示参数下，具有三个谐振工作点，如表2所示.

表2 串联谐振型IPT系统谐振工作点

三个谐振工作点对应的逆变器输出电压及原边谐振电流波形如图2所示.

这三个谐振点上，由(16)式可得系统雅可比矩阵特征值如表3所示.由表3可以看出，工作点1和3的特征值均分布在单位圆内，为稳定工作点，而工作点2有一个特征值分布在单位圆外，为不稳定工作点.

图2 逆变器输出电压及原边谐振电流稳态理论波形 (a)谐振点1;(b)谐振点2;(c)谐振点3

表3 系统谐振点雅可比矩阵特征值

4.2.仿真及实验验证

4.2.1.多谐振工作点验证

为了验证前面理论分析结果，在PSpice软件中建立了图1所示系统的仿真模型，以定频模式控制系统分别工作在各理论谐振频率点上，稳态时逆变器输出电压及原边谐振电流仿真波形分别如图3所示.

由图3可以看出，系统在各理论谐振点上均工作于ZCS软开关状态，对比图2和图3中各谐振点的稳态波形，可以看出符合得很好.另外当系统工作频率偏离各谐振点时，PSpice仿真结果发现系统将进入硬开关工作模式，因此，PSpice仿真结果说明本文方法的计算结果是准确有效的.

为了对理论结果进行实验验证，我们搭建了以图1所示电路为主电路的串联谐振型IPT实验系统，系统主要元器件参数测量值如表1所示.实验中，用信号发生器产生控制信号，该信号经驱动电路控制全桥逆变器的开关管.通过信号发生器扫频，我们得到实验系统的谐振工作点如表4所示.为了便于对比分析，表4中同时列出了理论计算结果、交流阻抗分析结果、PSpice仿真验证结果及实验测试结果.

图3 逆变器输出电压( )及原边谐振电流(◇)波形PSpice仿真波形 (a)谐振点1;(b)谐振点2;(c)谐振点3

表4 串联谐振型IPT系统谐振工作点(单位:kHz)

从表4可以看出，交流阻抗分析结果与本文的理论计算结果比较接近，但存在一定的偏差，而PSpice仿真结果与理论值完全一致，实验测试结果与理论结果也符合得很好，考虑到实验过程中存在参数漂移以及测量精度有限等问题，可以看出实验测试值与理论值基本一致.因此，由表4可知本文所提理论方法具有较高的准确性，计算结果更接近实际情况.

在各谐振点上，逆变器的输出电压及原边谐振电流实验波形如图4所示.

图4 逆变器输出电压及原边谐振电流波形实验波形 (a)谐振点1;(b)谐振点2;(c)谐振点3

对比图2至图4中各谐振点的电压电流波形可以看出，理论与实验波形基本一致，只是实验中由于开关管存在一定的导通压降及开通与关断时间，使得逆变器输出电压波形存在一定的畸变，使得加在谐振网络上的电压有效值有所偏低，但这并不影响系统的谐振工作频率.

4.2.2.谐振工作点稳定性验证

将系统切换到浮动频率控制模式以检验系统谐振工作点的自治振荡稳定性，这里为了更好地反映稳定性测试效果，我们设计了负载扰动实验，在稳态时通过开关电路给系统负载并联上一个阻值相同的电阻，然后再断开该并联电阻，从而形成一个50%的负载波动.负载扰动电路如图5所示.

图5 负载扰动电路

图6 负载扰动过程逆变器输出电压及原边谐振电流实验波形(下半窗口波形为上半窗口矩形选择框的局部放大波形)(a)扰动前;(b)扰动中;(c)扰动后

负载扰动实验中，逆变器输出电压及原边谐振电流波形如图6所示，图中上半部分为扰动过程波形图，下半部分为局部展开图，图6(a)—(c)分别显示了扰动前、扰动过程中及扰动后系统的稳态波形.

由图6所示的实验结果可以看出，浮频控制模式下，负载扰动前系统工作在谐振点3上，谐振频率为22.2 kHz;并联电阻后，系统的谐振频率受负载的影响变为26.7 kHz;负载扰动后，并联的电阻被断开，系统恢复到扰动前的参数，在扰动影响下，系统工作点切换到谐振点1并稳定运行，谐振频率变为29.4 kHz.因此，在谐振点1和3上，系统均可稳定运行，与理论分析的结果一致，这验证了本文自治振荡稳定性分析方法的正确性.

5.结 论

本文以串联型感应电能传输(IPT)系统为例，研究了IPT系统的多谐振点的判断及稳定性分析问题.文中建立了系统的频闪映射模型，根据不动点理论推导出了系统的稳态响应分段解析函数式，并在此基础上，给出了系统谐振工作点的理论判据，结合庞加莱映射的雅可比矩阵特征值分布情况，给出了谐振点的稳定性判据.结合具体实例系统，讨论了其多谐振点现象，并通过仿真和实验进行了验证，证明了本文理论分析结果的正确性.

值得注意的是本文的分析方法主要适用于分析系统的稳态谐振点及其自治振荡稳定性，对动态过程的动力学行为如负载切换过程中谐振工作点的变化尚不能描述，这还需在后续研究中进一步完善.

本文所提出的分析方法可以推广应用到其他类似谐振变换电路的建模及稳态工作点分析中，为谐振变换电路的研究提供一定的理论参考.

［1］ Ping S 2008 Ph.D.Dissertation(Auckland:The Univeristy of Auckland)

［2］ Yang Z，Liu W T，Basham E 2007 IEEE Trans.Magn.43 3851

［3］ Covic G A，Boys J T，Lu H G 2006 Proceedings of the 1st IEEE Conference on Industrial Electronics and Applications Singapore，May 24—26，2006 p466

［4］ Dehennis A D，Wise K D 2005 Journal of Microelectromechanical Systems 14 12

［5］ Green A W，Boys J T 1994 Proceedings of the 5th International Conferenceon Power Electronics and Variable-Speed Drives London，UK，Oct 26—28，1994 p694

［6］ Su Y G，Tang C S，Wu S P，Sun Y 2006 Proceedings of the International Conference on Power System Technology Chongqing，China Oct 22—26，2006 p794

［7］ Tang C S，Sun Y，Su Y G，Nguang S K，Hu A P 2009 IEEE Trans.Power Electron.24 416

［8］ Wang C S，Covic G A，Stielau O H 2004 IEEE Trans.Power Electron.19 995

［9］ Sun Y，Hu A P，Dai X，Su Y G.2004 Proceedings of the International Conference on Power System Technology Singapore，Nov 21—24，2004 p1015

［10］ Dai X， Huang X Y， SunY 2006 TransactionsofChina Electrotechnical Society 21 78(in Chinese)［戴 欣、黄席樾、孙 跃2006电工技术学报21 78］

［11］ Han T，Zhuo F，Yan J K，Liu T，Wang Z A 2005 Advanced Technology of Electrical Engineering and Energy 24 45 (in Chinese)［韩 腾、卓 放、闫军凯、刘 涛、王兆安 2005电工电能新技术24 45］

［12］ Hu A P 2001 Ph.D.Dissertation(Auckland:The University of Auckland)

［13］ Wang C S，Covic G A，Stielau O H 2004 IEEE Trans.Ind.Electron.51 148

［14］ Wu Y，Yan L G，Xu S G 2004 Proceedings of the CSEE 24 63(in Chinese)［武 瑛、严陆光、徐善刚2004中国电机工程学报24 63］

［15］ Wang X M，Zhang B，Qiu D Y，Chen L G 2008 Acta Phys.Sin.57 6112(in Chinese)［王学梅、张 波、丘东元、陈良刚2008物理学报 57 6112］

［16］ Li M，Ma X K，Dai D，Zhang H 2005 Acta Phys.Sin.54 1084(in Chinese)［李 明、马西奎、戴 栋、张 浩 2005物理学报54 1084］

［17］ Wang A Y，Ling Z H 2010 Chin.Phys.B 19 070506

［18］ Luo X S，Wang B H，Chen G R，Quan H J，Fang J Q，Zhou Y L，Jiang L Q 2003 Acta Phys.Sin.52 12(in Chinese)［罗晓曙、汪秉宏、陈关荣、全宏俊、方锦清、邹艳丽、蒋品群 2003物理学报 52 12］

［19］ Zhao Y B，Luo X S，Fang J Q，Wang B H 2005 Acta Phys.Sin.54 5022(in Chinese)［赵益波、罗晓曙、方锦清、汪秉宏 2005物理学报54 5022］

［20］ Chen Y S 1993 Bifurcation and Chaos Theory of Nonlinear Vibration Systems(Beijing:Higher Education Press)p109(in Chinese)［陈予恕1993非线性振动系统的分叉和混沌理论(北京:高等教育出版社)第109页］

PACS:84.30.Jc，05.45.－a

Analysis of multiple resonant operating points and their autonomous oscillation stabilities in inductive power transfer systems*

Tang Chun-Sen1)Sun Yue1)Dai Xin1)Wang Zhi-Hui1)Su Yu-Gang1)Hu Ai-Guo2)
1)(College of Automation，Chongqing University，Chongqing 400044，China)2)(School of Engineering，The University of Auckland，Auckland 1010，New Zealand)(Received 1 September 2010;revised manuscript received 10 November 2010)

In this paper we determine multiple resonant operating points(ROPs)of inductive power transfer(IPT)systems and perform the corresponding stability analysis of a series-tuned IPT system，which is taken for example，through using nonlinear dynamics theories.The stroboscopic mapping model of the system is built and a piecewise analytical function of the steady-state response is derived with the fixed-point theory.Then a criterion for assessing the system ROPs is given mathematically.The stability analysis of ROPs is achieved according to the locations of the eigenvalues of the Jacobi matrix of the Poincare mapping model of the system.A case study of the phenomenon of multiple ROPs is conducted，and both simulation and experimental results verify the theoretical results of the proposed method.Furthermore，the proposed method can provide useful theoretical reference for modeling and steady-state analysing other similar resonant converters.

inductive power transfer(IPT)，stroboscopic mapping，Jacobi matrix，stability

*中央高校基本科研业务费(批准号:CDJZR10170003)资助的课题.

E-mail:cstang@cqu.edu.cn

*Project supported by the Fundamental Research Funds for the Central Universities(Grant No.CDJZR10170003).

E-mail:cstang@cqu.edu.cn