基于模糊Box-Jenkins方法的电价建模与短期预测

蔡 宁，孟 濬，颜文俊

（浙江大学 电气工程学院，杭州 310027）

基于模糊Box-Jenkins方法的电价建模与短期预测

蔡 宁，孟 濬，颜文俊

（浙江大学 电气工程学院，杭州 310027）

由于单一的AR、MA和ARMA模型不能很好地匹配复杂的电价时间序列数据，因此传统的Box-Jenkins方法不能很好地进行电价预测。文章提出了基于模糊Box-Jenkins的电价建模和短期预测方法。引入模糊策略，生成分别对应Box-Jenkins方法中的AR，MA，ARMA三个模型的模糊因子，再通过模糊因子对三个模型进行模糊综合。对浙江省电力市场电价数据的仿真表明，在电价序列不能较好地匹配Box-Jenkins方法中各模型的情况下，模糊Box-Jenkins方法能取得更好的预测效果。

建模；短期预测；模糊；Box-Jenkins；电价

0 引言

电价预测是指在考虑市场供求关系、市场参与者的市场力、电力成本、电力市场体制结构以及社会经济形势等重要因素影响的条件下，利用数学工具对历史数据进行分析和研究，探索事物之间的内在联系和发展变化规律，在满足一定精度和速度的情况下，对未来电力市场中的电力交易价格进行预测。随着全球电力市场化的不断发展，电价在电力市场中的重要地位受到越来越多的重视。近年来学者们开始对电价进行比较深入的研究，提出了不少电价预测方法[1-4]。

Box-Jenkins方法[5]是由美国统计学家Box和英国统计学家Jenkins提出，并在社会、经济预测等领域取得了广泛的应用[6-10]。

在现实生活中，电价受诸多因素影响，例如政府政策和经济水平等，所以从本质上来说，电价预测问题是一个经济预测问题。传统的Box-Jenkins方法，利用时间序列的自相关函数和偏相关函数的特征，采用AR、MA和ARMA三种模型对时间序列进行建模识别。但电价数据往往是高度复杂，并且具有非线性、强耦合性，因此无法将现实数据采用某种线性模型进行精确描述。针对这一问题，本文采用模糊Box-Jenkins的方法，对电价序列进行建模和短期预测。采用模糊策略，对AR、MA和ARMA模型进行模糊综合。通过对浙江省电力市场电价数据进行仿真，结果表明，在电价序列不能较好地匹配Box-Jenkins方法中各模型的情况下，模糊Box-Jenkins方法能取得较好的效果。

表1 Box-Jenkins方法中模型选择

1 Box-Jenkins预测方法

Box-Jenkins法是通过分析现象随时间推移而变化的特征，以现象的历史统计资料为基础去建立时间模型，并进行外推预测。它以自相关函数、偏自相关函数的统计特性为依据，确定模型的类型(AR、MA和ARMA)，进而对模型进行定阶、参数估计、适应性检验并建立适应序列模型。

Box-Jenkins建模方法的步骤：

(1)数据处理：检验时间序列是否为平稳时间序列。若时间序列为非平稳时间序列。通过对序列进行差分和零均值的方法使序列平稳化。若{Yt}为非平稳时间序列，则进行差分处理：

其中n为样本数，s为周期。

进而进行零均值处理：

形成新序列Wt：

检验Wt是否为平稳序列。若不是，则继续进行差分和零均值处理，直至得到新的平稳时间序列。一般来说，差分迭代不会多于3次。

(2)模型选择：计算平稳时间序列的偏相关函数和自相关函数。例如偏相关函数是截尾的，而自相关函数是拖尾的，则该序列适合AR模型，模型选择方法如表1所示。

(3)参数估计：模型定阶主要依据F-判据准则对残差平方和进行比较，可以由低阶到高阶拟合模型，直到模型残差平方和的变化不显著为止。模型参数估计的方法有很多，其中有效的方法为最小二乘估计和极大似然估计。

(4)模型的检验：通过对残差序列的随机性进行检验，如果残差序列具有随机性，则说明试用模型是合适的，否则需要进一步改进。

(5)模型的预测：运用获得的模型进行相应预测，若时间序列的特性发生变化，需要对模型进行修改，甚至需要重新建模。

从上述步骤可以看出，Box-Jenkins法通过对时间序列进行平稳化处理来降低时间序列的复杂度。但对于复杂时间序列来说，平稳化处理之后，时间序列的复杂度依然较高，无法采用Box-Jenkins法获得较为精确的预测结果。因此，本文利用模糊Box-Jenkins法去解决上述相关问题。

2 模糊Box-Jenkins预测方法

为了克服Box-Jenkins预测方法存在的不足，使模型更加符合实际情况，本文在Box-Jenkins预测模型的基础上，加入模糊策略参数调整，通过自相关函数和偏相关函数的相关变化，对模型进行模糊整合。模糊Box-Jenkins预测系统结构见图1。模糊调节器的输入为平稳时间序列的自相关函数和偏相关函数，输出是对应AR模型、MA模型和ARMA模型的柔化系数。

2.1 模糊Box-Jenkins方法建模

首先，检验时间序列是否为平稳时间序列，一般需要消除时间序列的趋势因素和周期因素。根据公式1，先取s=1，进行一次差分和零均值处理，消除时间序列的趋势因素；再取s=T（T为时间序列的周期），消除时间序列的周期因素。通过对自相关函数和偏相关函数的“截尾”和“拖尾”显著性检验，来对模型的类别进行判断。采用F-判据准则和最小二乘估计方法对模型进行定阶和参数估计。

同时将自相关函数和偏相关函数作为模型的模糊输入，通过模糊规则的运算，得到AR模型、MA模型和ARMA模型的柔化系数，然后对三个模型进行模糊整合。

最后对模型进行残差序列检验，若检验成功，则可通过该模型进行预测，否则要继续对模型进行进一步改进。

2.2 模糊调节器设计

由于平稳时间序列相应的自相关函数和偏相关函数决定了系统的模型类别和模型阶数，因此自相关函数和偏相关函数分布反映了各个模型在实际模型中所占的比重。将自相关函数ρk和偏相关函数φkk进行模糊化处理，转换到模糊论域[-6,6]，同时定义 7 个模糊语言变量：“正大”（PB），“正中”（PM），“正小”（PS），“零”（0），“负小”（NS），“负中”（NM），“负大”（NB）。输入隶属度函数如图2所示。

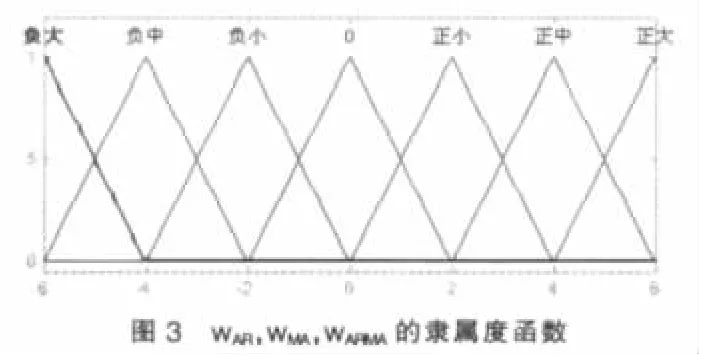
将输出量wAR，wMA，wARMA进行模糊划分，模糊论域为[-6,6]，同时定义 7 个模糊语言变量：“正大”（PB），“正中”（PM），“正小”（PS），“零”（0），“负小”（NS），“负中”（NM），“负大”（NB）。输出的隶属度函数如图3所示。

相应模糊规则为：

其中Ri是第i条模糊规则，φkk是序列的偏相关函数，ρk是序列的自相关函数wAR，wMA和wARMA分别是AR模型，MA模型，ARMA模型的柔化系数。

3 模糊Box-Jenkins算法的电价预测应用研究

为了验证算法的有效性，本文采用浙江电力市场2001年2月的电价数据进行仿真验证。电价数据采样间隔为半小时，电价的分布情况如图4所示。

首先采用2001年2月16日到2001年2月18日的电价序列进行仿真，研究电价序列的自相关函数和偏相关函数，发现其收敛速度较慢，因此可以判断该序列不是平稳时间序列，需要对该序列进行差分和平稳化处理。首先为了消除周期项对时间序列的影响，以周期长度作差分和零均值化处理；其次为了消除趋势项对时间序列的影响，对前后项进行差分和零均值化处理。原始序列的自相关函数如图5(a)所示，原始序列的偏相关函数如图5(b)所示，平稳化后的自相关函数如图5(c)所示，平稳化后的偏相关函数如图5(d)所示。从图中可以判定时间序列已经平稳。

分别运用传统Box-Jenkins方法和模糊Box-Jenkins方法对2001年2月16日到2001年2月18日的数据进行建模，然后对2001年2月19日的电价进行预测。预测结果如图6所示。

图5 平稳化前后的自相关函数和偏相关函数

图6 Box-Jenkins建模预测和模糊Box-Jenkins建模预测的对比

图7 Box-Jenkins建模预测和模糊Box-Jenkins建模预测的对比

运用同样的方法，取2001年2月23日到2001年2月25日的电价数据，分别进行Box-Jenkins预测建模和模糊Box-Jenkins预测建模，然后对2001年2月26日的电价进行预测，结果如图7所示。

仿真结果表明，模糊Box-Jenkins预测建模方法的结果要优于传统Box-Jenkins预测建模方法。由图6可以看出，当现实电价序列能够较好地匹配传统Box-Jenkins方法中的模型时，传统Box-Jenkins方法和模糊Box-Jenkins方法都能较好地对电价进行预测，通过误差计算，传统Box-Jenkins方法的误差约为3.5%，模糊Box-Jenkins方法的误差约为2.6%；由图7可以看出，当现实电价序列较为复杂，Box-Jenkins方法中的模型不能完全对其进行描述时，通过误差计算，传统Box-Jenkins方法的误差约为14%，模糊Box-Jenkins方法的误差约为4.3%。

4 结论

本文对传统Box-Jenkins方法进行了深入研究，针对其预测复杂电价序列能力不足的问题，进行了相应的改进，提出了模糊Box-Jenkins方法。新方法克服了传统Box-Jenkins方法对复杂非线性序列的模型选用问题，通过加入模糊策略层，对传统模型进行模糊综合。仿真结果表明，模糊Box-Jenkins方法的预测精度较传统的Box-Jenkins方法高。模糊Box-Jenkins方法目前还是对Box-Jenkins方法进行算法结构上的改进，没有考虑到现实中的各种因素对模型的影响，以后的研究中可考虑在模型中引入外界因素扰动，对模型进行修改，进一步提高模型的预测精度。

[1]X.Lu,Z.Dong,X.Li.Electricity Market Price Spike Forecast with Data Mining Techniques[J].Electric Power Systems Research,2005，(1).

[2]R.Pino,J.Parreno,A.Gomez,P.Priore.Forecasting Next-day Price of Electricity in the Spanish Energy Market Using Artificial Neural Networks[J].Engineering Applications of Artificial Intelligence,2008，1（21）.

[3]姜巍，王富忠，沈祖志.基于多智能体的短期电价智能预测方法[J].电力系统及其自动化,2007,31(4).

[4]张春辉，闵勇，丁仁杰等.级联相关的神经网络模型在边际电价预测中的应用[J].电力系统及其自动化,2003,27(3).

[5]B.George,G.M.Jenkins.Time Series Analysis,Forecasting and Control，Revised Edition[M].Oakland，CA：Holden-Day，1997．

[6]J.Gillberg,L.Ljung.Frequency-domain Identification of Continuous-time ARMA Models from Sampled Data[J].Automatica,2009,6(45).

[7]R.Pintelon,J.Schoukens.Box–Jenkins Identification Revisited—Part I:Theory[J].Automatica,2006，1（42）.

[8]R.Pintelon,Y.Rolain,J.Schoukens.Box-Jenkins Identification Revisited—Part II:Applications[J].Automatica,2006，1(42).

[9]B.H.Goh,H.P.Teo.Forecasting Construction Industry Demand,Price and Productivity in Singapore:the Box-Jenkins Approach[J].Construction Management and Economics,2000，5（18）.

[10]Y.Lu,S.M.Abou Rizk.Automated Box–Jenkins Forecasting Modeling[J].Automation in Construction,2009，5（18）.

（责任编辑/浩 天）

TP271

A

1002－6487（2011）03－0167-03

国家高技术研究发展计划（863）（2007AA05Z232）；浙江省科技计划项目（2007C21180）

蔡 宁（1986-），男，浙江三门人，硕士研究生，研究方向：复杂系统的智能建模、控制。