基于Copula理论的投资组合风险测度

赵 鹏

（西安交通大学 经济与金融学院，西安 710061）

基于Copula理论的投资组合风险测度

赵 鹏

（西安交通大学 经济与金融学院，西安 710061）

文章基于现代前沿的Copula理论，以中国股市八个行业板块指数的组合为研究对象，构建了Copula-GARCH模型，得到了更加准确的组合收益联合分布函数。通过蒙特卡洛模拟法获得投资组合的VaR，回测检验表明Copula-GARCH模型能够较Riskmetrics和历史模拟法的更加准确地描述组合风险。这为我们在国内股票市场上应用Copula理论管理证券投资市场风险提供了理论依据。

Copula；中国股市；市场风险；金融风险管理

0 引言

随着计算机技术的日新月异，一种早在上世纪五十年代就被提出却在技术上难以应用的理论——Copula理论，在金融领域尤其是市场风险管理领域的应用研究得以迅速发展。1959年，Sklar提出可以将一个联合分布分解为k个边际分布和一个Copula函数的观点[1]。Nelsen（1998）对Copula作了系统的介绍[2]，而张尧庭将Copula理论引入国内[3][4]。

在经典的证券投资组合理论中，资产组合的风险由系统风险和非系统风险组成，其中非系统风险即单个证券的风险由其本身的属性来确定，而系统风险则由组合内各证券资产的相关结构来决定，这个相关结构由协方差矩阵来描述。不过限于线性和正态假设，协方差矩阵方法在实践中无法刻画金融资产波动的尖峰厚尾分布特征。在引入Copula函数后，我们就可以刚好把投资组合的整体风险按照系统风险和非系统风险进行分解，系统风险即资产组合的结构风险可以由一个Copula函数来描述，而非系统风险即单个证券的市场风险可以由成熟的单变量时间序列波动模型（如EWMA、GARCH）来刻画。本文将以中国股票市场八个行业板块指数为实证研究对象，通过应用Copula理论来获得资产组合的VaR（在险价值），为金融机构管理国内股票投资的市场风险提供应用理论依据。

1 Copula函数的选择、估计与检验

1.1 Copula函数的选择

在多变量的金融应用研究中，我们最常用的是正态Copula函数和t-Copula函数。

⑴多元正态Copula分布函数的表达式为

其中，ρ为对角线上的元素为1的对称正定矩阵，Φρ表示相关系数矩阵为ρ的标准多元正态分布，Φ-1()表示标准正态分布函数的逆函数。

⑵多元t-Copula分布函数的表达式为

其中，ρ为对角线上的元素为1的对称正定矩阵，Tρ,v表示相关系数矩阵为ρ、自由度为v的标准多元t分布，tv-1(ui)(i=1，2，…，N)为自由度为v的一元t分布的逆函数。

1.2 Copula函数的估计

Copula函数的估计方法一般包括极大似然估计法（ML）、边际分布推导法（IFM）[5]和规范极大似然法（CML）。 在变量维数很高时，极大似然法会显得参数过多，IFM法将边际分布参数的估计和Copula函数参数的估计分成两个阶段进行，比ML法要简化许多，但也容易产生边际分布模型的设定错误。CML法不对边际分布作任何假设，在IMF法的第一步中用经验分布代替边际分布。Okaes[6]对此专门做过研究，其结论是只要边际分布形式符合实际，CML方法较前两种方法更加精确。因此在本文的实证研究中采用CML法进行Copula函数参数的估计。

1.3 Copula函数的检验与选优

对于估计得到的Copula函数，我们需要进行拟合优度检验以确定其有效性。在本研究中，我们采用K-S检验。KS检验是非参数检验，统计值T定义为经验累积分布函数与理论累积分布函数之间的最大差异其中，为经验 Copula 函数[7]，F(x)为理论 Copula 函数。

2 边际分布的选择与Copula-GARCH模型的构建

根据Copula理论，在确定了描述资产相依结构的Copula函数后，只要能够确定各资产变量的边际分布，即可获得整个资产组合的联合分布，进而计算出资产组合的VaR。大量的金融时间序列研究发现，金融时间序列的波动分布是随时间变化的，存在着明显的波动聚集效应，而GARCH族模型是目前最成熟的单变量金融时间序列波动模型，因此在本研究中，我们采用GARCH族模型来刻画联合分布的条件边际分布。于是，我们可以构建出描述投资组合收益联合分布的Copula-GARCH模型：

假设{y1t}t=1T,…,{yNt}t=1T为N个服从GARCH过程的随机变量，结合Copula理论，我们可以得到N元Copula-GARCH模型：

其中C为任意形式的N元条件Copula函数，Fnt为联合分布的边际分布，随机干扰项ξ1t,…,ξNt可以是服从独立同分布的标准t正态分布、标准t分布或其他分布。根据（3）式，我们得到y1,…,yN的联合分布：

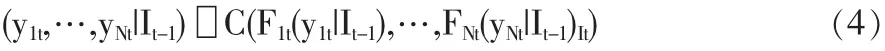
3 Copula函数的模拟与VaR计算

对于大多数的Copula函数，其相应的逆函数的解析式一般很难求出，因此我们常采用蒙特卡罗模拟法来实现VaR的计算。完整的基于Copula理论的多资产投资组合VaR计算的步骤为：⑴确定恰当的Copula函数C和边际分布Fn(x)的形式并估计分布参数，组建基于Copula的联合分布模型；⑵根据多元Copula仿真技术生成边际分布随机数；⑶根据，rn=Fn-1(un)得到与边际分布随机数对应的资产收益；⑷计算投资组合的收益，由此得到投资组合未来收益的一个可能情景；⑸重复步骤⑵~⑷k次，得到k个投资组合未来收益的可能情景，从而获得投资组合未来收益的模拟经验分布，给定置信水平α，即可根据P{rp≤-VaR}=α，得到投资组合的VaR。

4 实证研究

4.1 Copula-GARCH模型的参数估计与检验

4.1.1 样本的选取

本研究选取了沪深300材料指数（399909）、300工业指数 （399910）、300 公 用 指 数 （399917）、300 金 融 指 数（399914）、300 能源指数 （399908）、300 消费指数（399912）、300信息指数（399915）和 300医药指数（399913）八个行业板块指数的日收益率作为研究对象。研究所需原始数据来源于中证指数有限公司发布的自2007年9月26日至2009年12月31日的552组交易日的历史收盘价。根据收益率计算公式，共得到551组收益率样本观测值。其中，2009年8月5日前的451组观测值用于估计参数，之后的100组观测值用于回测检验。

4.1.2 Copula函数的估计

我们采用规范极大似然法（CML）估计八个指数的Copula函数，得到结果见表1、表2。

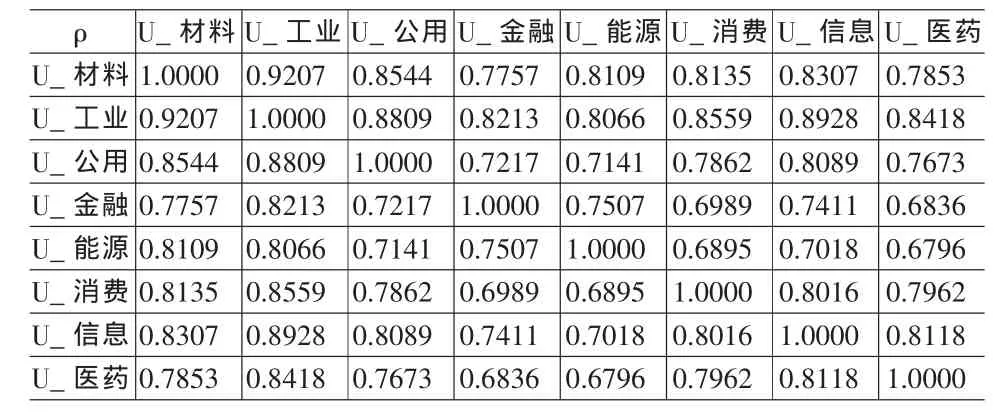
表1 正态Copula函数的参数矩阵ρ的估计结果

表2 t-Copula函数的参数矩阵ρ的估计结果

4.1.3 Copula函数的拟合优度检验

我们对估计出的正态Copula函数和t-Copula函数进行K-S检验，得到的结果如表3。

从K-S检验的结果看，正态Copula函数和t-Copula函数的K-S检验的相伴概率p值分别为0.4310和0.3397，均通过了显著性水平0.05的K-S检验，因此两个Copula函数均可用于描述投资组合内部的相依结构。

4.1.4 边际分布模型的选择与参数估计

⑴均值方程的确定

经我们对八个行业指数的收益率作ADF平稳性检验、滞后20阶的序列自相关检验以及对各指数收益率的GARCH过程进行拟合检验后可以确定：（5）式均可作为各指数收益率GARCH模型的均值方程

检验表明，对于各行业指数，通过选择合适的方差方程，（5）式的残差序列不再存在序列自相关和ARCH效应。

⑵方差方程的确定

我们用GARCH族模型对各行业指数收益率进行拟合。根据AIC和SC信息准则，经过比较选择，我们确定八个行业指数收益率GARCH模型的方差方程类型见表4。

由此可见，行业指数收益率所服从的条件分布各不相同。根据Eviews软件的计算，我们得到各行业指数收益率的GARCH模型参数估计检验结果如表5。

从均值方程的估计检验结果看，各均值方程的截距项在0.05的水平下均不显著，说明在观测阶段，行业指数收益率与零值无统计上的差异；从方差方程的估计检验结果看，各方差方程的GARCH项系数、ARCH项系数以及杠杆系数均通过了显著性水平0.05的检验；我们对均值方程的残差项进行了检验，发现各估计方程的残差项均不再存在自相关和ARCH效应，因此我们认为，估计出的GARCH族模型可以用来描述实际资产收益率序列的波动。

表3 理论Copula函数的K-S检验

表4 各行业指数条件方差方程的选择

表5 行业指数收益率GARCH模型参数估计检验结果

表6 不同方法得到的T+1日投资组合VaR结果比较 （单位：%）

上文中，我们确定了描述资产收益间相依结构的Copula函数，也确定了各资产收益的边际分布，下面即可通过进行蒙特卡罗模拟法计算投资组合的VaR。

4.2 投资组合VaR的计算与回测检验

4.2.1 未来收益分布的模拟与VaR计算

为便于说明，我们令用于计算的观测样本最后一日即2009年8月5日为T日。设第T+1日的初始总投资为1，对各行业指数的资金投入平均分配。首先，按照选定的Copula函数生成10000个随机数，即对应10000个可能的情景，并以各边际分布的GARCH模型模拟推算各行业指数T+1日的收益率，最后计算出T+1日的投资组合收益率。经过仿真计算，得到以正态Copula-GARCH模型和t-Copula-GARCH模型（ν=8.6262）分别模拟得到的T+1日的投资组合收益率分布直方图如图1所示。

经统计检验，两个分布的峰度分别为3.4296和3.4214，J-B统计值分别为79.44和75.64，均显著不同于正态分布，这符合经验收益分布的尖峰、厚尾特征。从图形直观地观察，由两个Copula-GARCH模型分别模拟得到的投资组合收益率分布的差异较小。之后对分别得到的模拟数据进行排频，并根据设定的置信水平得到投资组合T+1日的风险值VaR。这里设定置信水平分别为95%，97.5%和99%，得到的模拟结果如表6。为便于比较，我们同时给出了历史模拟法和Riskmetrics参数法的计算结果。

可以看到，由历史模拟法得到的VaR的绝对值在4个不同的置信水平下均是最大的，以正态假设为基础的标准Riskmetrics参数法计算得到的VaR的绝对值在4个不同的置信水平下均是最小的，而由Copula-GARCH模型模拟得到的结果介于前二者之间。

4.2.2 回测检验及模型的比较

为确定究竟哪种方法更加准确，需要进行回测检验。分别以上述四种方法计算了自T+1日至T+100日的8个行业指数投资组合的VaR，其中历史模拟法和Riskmetrics法以经验数据推算，Copula-GARCH方法以蒙特卡罗模拟法推算投资组合收益未来100天的10000条路径，然后对模拟得到的每日的投资组合收益率进行排频，最后根据设定的置信水平得到VaR。自T+1日至T+100日共100天的VaR回测结果见图2和表7。

表7 八行业指数投资组合的VaR回测检验结果

回测结果分析：

⑴在95%的置信水平下，由历史模拟法、Riskmetrics、正态Copula-GARCH及t-Copula-GARCH蒙特卡罗模拟四种方法预测得到的VaR在后来的100天内分别失败了3次、6次、5次和5次，回测结果均通过了Kupiec检验，可见在95%的置信水平下，上述四种方法都可以用来预测投资组合的VaR。从LR统计量的相伴概率p值来看，两个Copula-GARCH模型的表现最好，而Riskmetrics模型也表现良好，历史模拟法则稍劣于前三种模型。

从经济角度看，以Riskmetrics方法计算VaR最节约风险资本，运用Copula-GARCH模型较Riskmetrics方法要平均增加8.83%的风险准备，以历史模拟方法进行风险控制的机构则需要较Riskmetrics方法增加37.89%的风险准备。

⑵在97.5%的置信水平下，由四种方法预测得到的VaR在后来的100天内分别失败了2次、5次、4次和4次，回测结果也都通过了Kupiec检验。从LR统计量的相伴概率p值来看，历史模拟法表现最好，两个Copula-GARCH模型的表现也不错，而Riskmetrics模型则稍显低估了风险。

从经济角度看，以Riskmetrics方法计算VaR仍然最节约风险资本，运用正态Copula-GARCH模型或t-Copula-GARCH模型较运用Riskmetrics方法要平均增加11.72%和12.44%的风险准备，而以历史模拟方法进行风险控制的机构需要较Riskmetrics方法增加38.04%的风险准备。

⑶在99%的置信水平下，由四种方法预测得到的VaR在后来的100天内分别失败了0次、4次、1次和1次，Riskmetrics方法不能通过显著性水平为0.05的Kupiec回测检验，已不能运用于中国股票市场投资组合的风险控制。从LR统计量的相伴概率p值来看，正态Copula-GARCH及t-Copula-GARCH模型的表现一样好，由其计算出的VaR正好覆盖了后来100天内的99天的风险，而历史模拟法又再次表现出一定的高估风险的迹象。

从经济角度看，由于Riskmetrics方法已不能准确刻画99%置信水平下的投资组合风险，因此我们只比较其他三种方法。从得到的VaR的均值看，正态Copula-GARCH模型在三者中是最经济的，但运用t-Copula-GARCH模型也仅仅较前者平均增加1.57%的准备金，而以历史模拟方法进行风险控制的机构则需要较运用正态Copula-GARCH方法的机构增加22.16%的风险准备资本金。

5 结论

在本研究中，历史模拟法无论是在三种置信水平下都是经济成本最高的模型，这与观测期内有较多大的波动而回测期内波动减小有直接关系。从VaR的回测图形及标准差可以看出，由历史模拟法得到的VaR变动很小，不能快速反映市场风险的变化，这样，当市场从大波动期向小波动期转换时，历史模拟法会高估市场风险，增大金融机构成本，而在市场从小波动期向大波动期转换时，又会低估市场风险，引发金融机构风险。

其他三种模型均可快速反映市场波动的变化。基于正态资产收益分布正态假设的Riskmetrics模型在较低的置信水平下是良好的、经济的风险控制模型，但其缺点是在高置信水平下会明显低估市场风险，这对于金融机构是危险的。而正态Copula-GARCH模型和t-Copula-GARCH模型虽然没有Riskmetrics模型经济，但其在各置信水平下都能比较准确地覆盖风险，综合比较起来，Copula-GARCH模型是金融机构测度投资组合VaR的理想方法。就这两种Copula-GARCH模型而言，两个模型的波动刻画能力在总体上差异很小。正态Copula模型在计算时相对容易，而t-Copula模型则对市场极端的波动更加敏感一些，二者各有优劣，金融机构可根据自己的偏好选择使用。

[1]Sklar A.Fonctions de RepartitionànDimensionsetLeurs Marges[J].Publication de l'Institut de Statistique de l'Université de Paris,1959,(8).

[2]Nelsen R B.An Introduction to Copulas[M].New York:Springer,1998.

[3]张尧庭.连接函数技术与金融风险分析[J].统计研究,2002,(4).

[4]张尧庭.我们应该选用什么样的相关性指标[J].统计研究,2002,(9).

[5]Durrleman V,Nikeghbali A,Roncalli T.Which Copula is the RightOne?[C].Working Paper，Groupe de Recherche Operationnelle.Credit Lyonnais，France，2000.

[6]Okaes D.Semiparametric Inference in a Model for Association in Bivariate Survival Data[J].Biometrika，1986，73(2).

[7]Deheuvels P.A Non-parametric Test for Independence[J].Publications de 1’Institut de Statistique de 1’Universite de Paris,1981,(26).

（责任编辑/浩 天）

F224.9

A

1002－6487（2011）03－0037-04

赵 鹏（1976-），男，河南郑州人，博士研究生，研究方向：金融理论与货币政策、金融风险管理。