基于角度和多普勒频率信息的动福射源的无源定位研究
乔 梁
(广东金融学院 计算机系,广州 510520)
单站无源定位技术因为具有隐蔽性和具有高度的独立性等特点而受到重视[1-4],并且在现代电子战和无线通信系统中都有广泛应用.传统的只测角单站无源定位技术只利用了目标的角度信息.这种方法的跟踪收敛速度慢、精度低,而且要求观测平台有一定的机动飞行,这为该技术的应用带来诸多的不便.因此研究增加辅助信息实现对运动目标的快速、无机动定位成为单站无源定位领域的发展趋势.这些辅助信息中包括目标辐射源信号的空域变化率信息(角度变化率)和频域变化率信息(多普勒频率及其变化率).研究结果表明增加角度变化率信息和多普勒频率及其变化率信息可以克服传统的只测角单站无源定位的缺点,更好地实现对运动辐射源的定位与跟踪.
1 系统方程的建立
1.1 系统状态方程
假设辐射源辐射等周期(周期Tr恒定)的脉冲信号,观测站每接收N个脉冲做一次观测,则T=NTr为采样间隔.
设Xk=1/fT]为三维条件下辐射源k时刻状态矢量,目标作一定加速度扰动下的匀速运动,观测站位于坐标原点,得到辐射源状态方程为
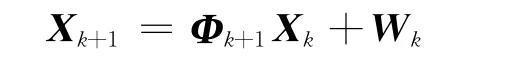
式中,fT为目标辐射信号载频.
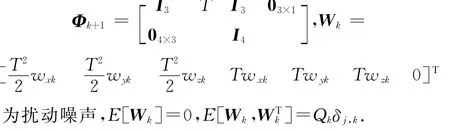
1.2 系统测量方程
由于多普勒效应,观测站得到的辐射源频率中包含了多普勒频率fdk.即

三维情况下fdk的表达式为

式中,vrk为k时刻目标相对于观测站的径向速度.
另外,对上式两边求导得

对上式化简并考虑到目标距离很远时,通常不会有大的机动,所以可以考虑目标作匀速运动,所以:

目标的方位角、俯仰角、方位角变化率、俯仰角变化率和多普勒频率及其变化率是常用的无源定位观测量,在这里我们称它们为空域变化量和频域变化量.由方位角、俯仰角、方位角变化率、俯仰角变化率的定义,得到测量方程:
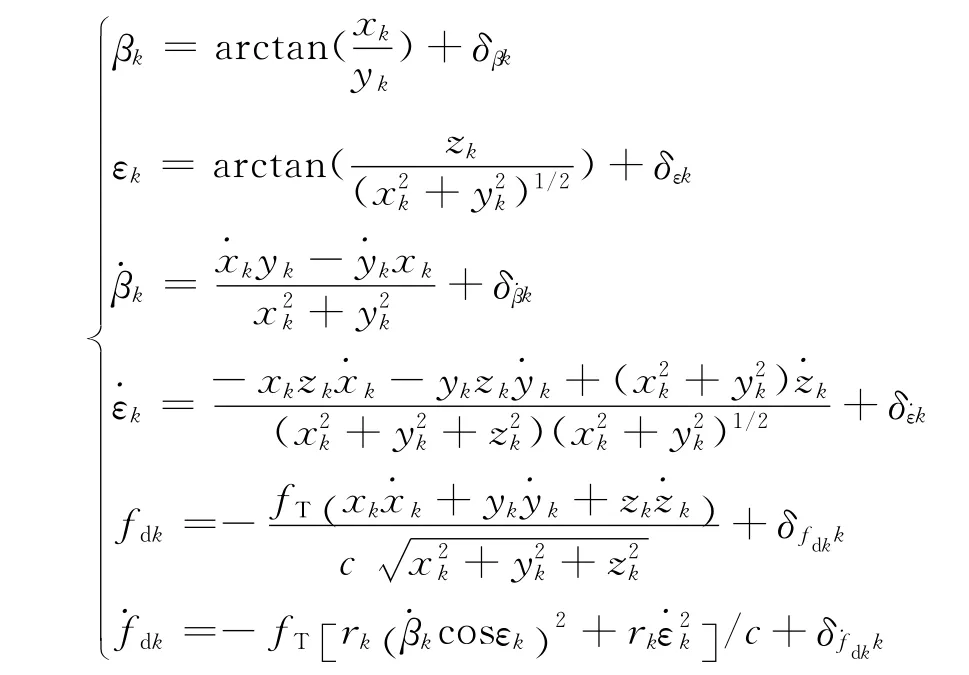
将上式写成矩阵形式为
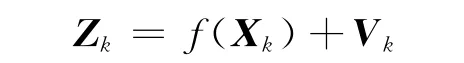
式中,Zk为测量矩阵;f(Xk)为状态矢量的实值向量函数;Vk为测量噪声,其协方差矩阵为Rk=E[].
1.3 测量方程的线性化
因上面的方程都是非线性的,需对其进行线性化处理.以俯仰角表达式为例,将其在预测点k/k-1处进行Taylor级数展开并取一次项,可以近似得出

用同样方法可以对其它表达式进行线性化处理.
经过上述分析,我们建立了测量量与目标状态之间的关系,应用修正增益的扩展卡尔曼滤波算法就可以实时得到目标状态的滤波估计值,从而实现对目标的定位跟踪.
2 定位算法分析
无源定位通常都是非线性问题,而对非线性滤波最经典的算法是扩展卡尔曼滤波[5-8].但是因为EKF算法存在协方差容易出现病态,以及对初始状态假定精度敏感等缺点,所以一些学者提出了MGEKF(修正增益的扩展卡尔曼滤波)算法.MGEKF滤波方法在大量实践中被证明是一种对非线性系统较好的滤波算法.
MGEKF算法如下:
(1)计算预测方程:
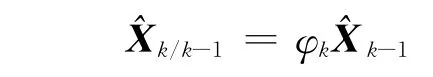
(2)计算预测协方差:

(3)计算 Kalman增益

(4)计算滤波方程:

(5)计算估计误差的协方差:
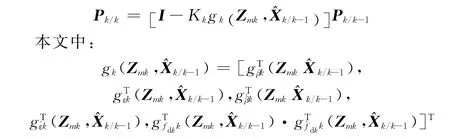
由前面分析可知,这些量均为已知.
3 计算机仿真

从图1仿真结果可以得到以下结论:通过测量频域和空域参数可以实现无机动单站对运动辐射源的无源定位跟踪,且定位误差可以收敛到很小.加入角度变化率和多普勒频率变化信息后,利用测量子集2和3的定位结果,其性能要优于子集1.

图1 相对位置误差曲线
4 结 语
实现对辐射源的单站无源定位具有非常重要的意义.本文主要讨论了单站无源定位与跟踪,并提出了一种改进的无源定位与跟踪算法.该算法不仅克服了传统的卡尔曼算法的不足,而且计算比较简单,实现容易,具有很强的实用性.经过一定次数的迭代滤波,在较短的时间内可将定位误差减到几百米以内.理论分析和仿真结果表明,通过测量频域和空域参数可以实现无机动单站对运动辐射源的无源定位跟踪,而且定位误差可以收敛到很小.这种方法使单站被动定位跟踪技术的研究走上了新台阶,拓宽了应用范围.尽管本文的方法还存在着一定的局限性,但仍不失为一种好的定位手段.
[1]郭广寒,王志刚.一种改进的粒子群算法[J].哈尔滨理工大学学报,2010,12(2):31-34.
[2]冯道旺,李宗华.一种单站无源定位方法及其可观测性分析[J].国防科技大学学报,2004(1):68-71.
[3]满春涛,盛桂敏.改进的协同粒子群优化算法[J].哈尔滨理工大学学报,2010,15(5):51-53.
[4]罗景青,刘文山,俞志富.对运动辐射源的单站无源定位技术研究[J].解放军电子工程学院学报,2000(2):9-11.
[5]李群力,傅妍芳.基于Kalman滤波的数据融合研究[J].计算机仿真,2007,24(8):299-302.
[6]郭艳丽,杨绍全.差分多普勒无源定位[J].电子对抗技术,2002,17(6):20-23.
[7]王 鼎,曲阜平,吴 瑛.一种基于空域和频域信息的固定单站无源定位跟踪改进算法[J].电子与信息学报,2007,29(12):2891-2895.
[8]汪语哲,史小平,朱 胤.抑制闪烁噪声的SMM-IUKF目标跟踪算法[J].哈尔滨理工大学学报,2010,15(5):69-74.
——2022 F1意大利大奖赛

