水声传感器网络节点自定位的遗传算法优化研究

谢远党，徐荣伟，张 华

（1.浙江海洋学院机电工程学院，浙江舟山 316004;2.舟山万达船舶设计有限公司，浙江舟山 316101）

无线传感器网络应用中，重要的是监测目标的具体位置，没有确切监测消息的位置没有任何意义。按照定位过程中是否需要测量节点之间的实际距离，把定位算法分为，基于距离的定位算法和距离无关的定位算法。距离无关的定位机制定位性能受环境因素的影响小，虽然定位的误差相应有所增加，但定位精度能够满足多数传感器网络的应用要求，是目前大家普遍重点关注的定位机制[1-2]。

质心算法是一种仅基于网络节点连通性的定位算法，定位精度取决于信标节点的密度和分布。许多人针对质心算法提出了改进，文献[3]中提出一种采用最小二乘原理构建的加权定位算法思路，该算法需要测距误差的均方值；文献[1]提出一种密度自适应的HEAP算法，通过在信标节点密度低的区域增加新标节点，以提高定位的精度；文献[4]中提对距离无关的几种定位机制进行了比较，信标节点密度的大小影响了定位精度的高低。陆地传感网一样，水下无线传感网中，节点的位置信息同样是数据采集必不可少的一部分。水声传感器网络是陆地无线传感器网络概念向水下应用的延伸,由多个传感器节点组成。

1 水声通信网络概述

水声通信是利用声波在海水里传播实现的。基本工作原理是先将文字、语音、图像等信息转换成电信号，进行数字化处理，换能器又将电信号转换为声信号进行发送；声信号通过水介质，将信息传递到接收换能器，声信号转换成电信号，解码器将数字信息解码，再将信息变成声音、文字及图片。

水声通信网络的研究起步于20世纪90年代。美国计算机学会从2006年开始成立了国际工作组，专门开展水下声传感器网络的研究和交流。美国的多所著名大学，都开展了水下声传感器网络课题的专门研究工作[5-6]。国内，水声传感器网络方面的研究也才刚刚开始，2006年，哈尔滨工程大学、北京科技大学等研究单位在863计划的支持下，结合多年水声通信的研究经验，开展水下声传感器网络的相关研究[7-9]。目前的水声传感器网络主要有两种拓扑结构，即二维水下传感器网络和三维水下传感器网络[10]。在二维水声传感器网络的系统模型中，传感器节点被放置在海洋底部,主要应用于海洋环境的监测和海底板块构造的研究领域。文献[11]讨论了在传感器网络节点自定位问题，并分RANGE，AOA，AOA+RANGE，AOA+COMPASS，AOA+COMPASS+RANGE几种情况进行探讨，证实了传感器网络能够定位并传输数据。

从现有的文献来看，对水声无线传感器网络节点自定位的问题开展比较少，陆地上无线传感器网络自定位相对较多。水下传感器网络二维模型如图1，本文主要研究水下传感器网络二维情况下节点的自定位问题，采用遗传算法优化节点自定位的精度，实现节点自定位的优化控制。

图1 水下传感器网络二维分布模型Fig.1 Sensor water under distribution network model of a two-dimensional sensor

2 定位数学模型

从现有的文献和研究来看，陆地上无线传感器网络以随机抛洒形式分布，包括均匀分布、高斯分布、瑞利分布等，其中以高斯分布最常见。在探讨无线传感器网络节点自定位以及节点覆盖的绝大部分的文献中，对节点的信号传播模型采取了圆形无线信号传播模型，节点分布选取均匀分布，在实际使用中，无线信号的传播模型是按信号传输强度的等高线分布，与理想的圆形模型有很大区别，因而也会造成节点自定位的误差，然而水声无线传感器网络的节点分布的复杂程度远远超过了陆地，比如信标节点自身的位置信息，陆地上的节点可以携带GPS等测量仪器，在水下却不能采取同样方式实现。文献[12]概述了目前水声传感器网络的应用前景和所面临的挑战，并对短距离声通信和MAC协议等进行了讨论，本文选取节点为均匀分布模型，通信模型取椭圆形模型，以替代等高线模型，减少通信模型对节点自定位的误差。

假定研究对象为二维平面，区域大小为xlength×ylength，其中xlength，ylength分别是该坐标对象的横坐标长度和纵坐标长度；随机布撒数量为N的节点作为信标节点，各个节点通过相互通信获得坐标或者网络中的位置等信息，各节点坐标分别为Pi（xi，yi），（i=1，2，…，n），信标节点均匀分布；随机布撒未知节点，数量为m个，未知节点坐标为Xj（xj，yj），（j=1，2，…，n）；对每个未知节点而言真实坐标跟估算坐标以及质心坐标都不相同，设某未知节点坐标X（xest，yest），与其通信的信标节点按质心算法建成一个质心坐标X（xav，yav），它们之间存在误差值，

图2 传感器节点初始分布及等高线模型Fig.2 Distribution of sensors node initial and equal altitudes line model

Δx；Δy分别表示信标节点构建成质心坐标值与未知节点真实值之间的误差。f（x，y）表示未知节点与信标节点之间距离，如下

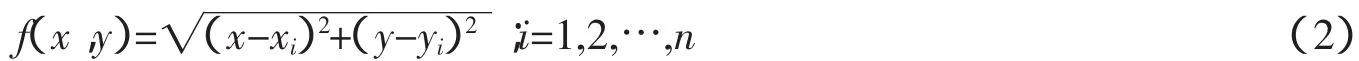
从数学角度而言，只有公式2知道了2个信标节点坐标和距离公式，在满足满秩的情况下，一定能够求解出未知节点的坐标，然而实际上，由于节点本身的限制，比如计算能力，通信干扰，使得实测数据中坐标以及距离都存在一定的误差，因而采用公式2进行求解带来一定的误差，导致定位精度较低。泰勒级数的实质是采用切线逼近方式求解方程的解，本文拟采用泰勒级数对距离公式进行变换求解。多元泰勒级数展开形式见公式3，其中第二行表示拉格朗日余项。

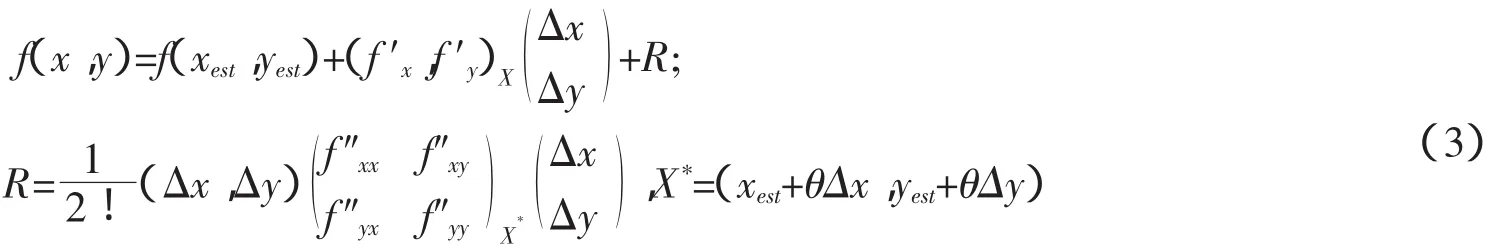
对公式2在未知节点真实坐标处X（xest，yest），用多元泰勒级数展开，公式2分别对x，y求一阶偏导数，

则公式2在未知节点X（xest，yest）处的泰勒级数展开如下，

公式5中，右侧两项分别表示如下

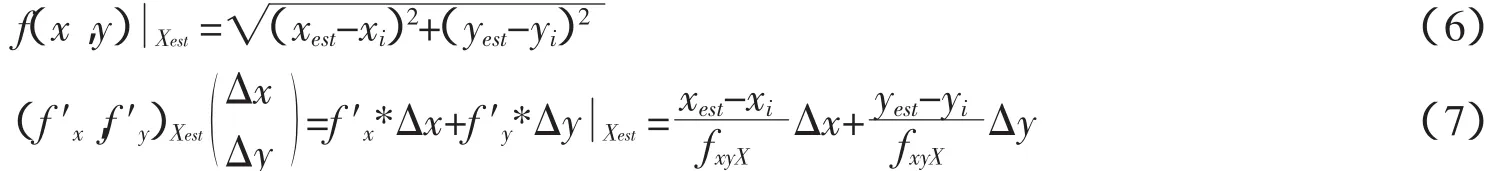
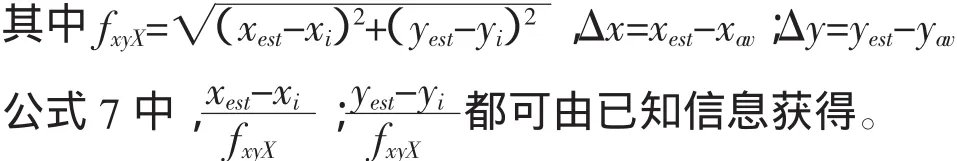
3 遗传算法下节点自定位及优化

3.1 优化设计

遗传算法是是一种高效、并行、全局搜索的方法，对于复杂的优化问题无需建模和进行复杂运算，只需要利用遗传算法的算子就能寻找到问题的最优解或满意解。采用遗传算法对节点自定位进行优化是目前研究节点自定位方面的一个研究方向，纵观现有的研究采用遗传算法的传感器网路节点自定位文献来看，针对陆地上的节点自定位的研究比较多[1,3,7,9]，由于陆地环境和水下环境不同，陆地上的现有的研究设计环境及优化不一定适合于水下，而针对水下传感器节点的自定位比较少，水下的环境比较复杂，影响节点自定位的因素也很多，本文主要考虑二维空间的情况。

在水下某区域布置传感器节点，假设节点能够通过某种方式布置在同一的深度位置，节点位置不随着洋流，扰动等因素发生变化，节点之间能够水声方式进行有效的通信，信标节点能够通过某种方式(如通过浮标等)获得自身的各种信息，从大规模布置节点，信标节点和浮标的制作，从经济等角度来看，目前还不适合大规模布置所有节点都是信标节点，因而少部分信标节点大部分为未知节点是目前现有的方式之一[10-14]，将该模型简化成在一个二维空间中，已知若干节点坐标，对其余一些节点进行坐标的位置的确定。遗传算法的最重要的特点之一是，仅仅关注适应度函数本身，而对具体是什么样的问题不作关心，将水下二维节点自定位问题简化，等效，然后可以用遗传算法对其进行寻优。按公式（1-7）取适应度函数如下：

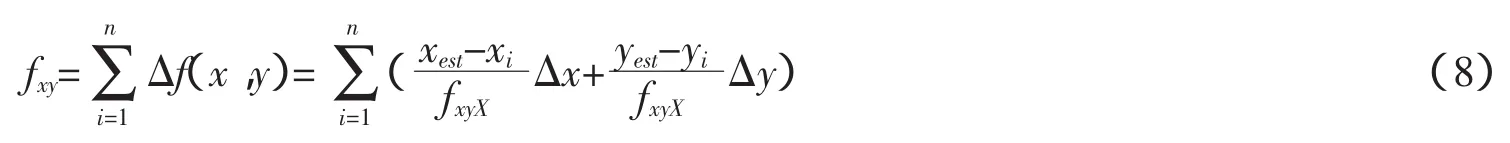
步骤设计

开始，节点初始化，信标节点相互之间通过交换信息，获知各自在网络中的位置等信息，然后向外界不断广播自身的信息，未知节点接收信息。

1）随机产生NIND个个体作为初始种群，每个个体为二维向量，每个二维个体含有PRICE个基因位，因而初始种群构成了NIND*(2*PRICE)大小的矩阵；二维向量代表了未知节点的坐标估计位置；

2）初始种群转换为十进制，并按公式10计算每一个个体的适应度函数值；

3）对函数值按适应度大小进行排序；适应度较高的个体被遗传到下一代的概率较大，适应度较低的个体被遗传到下一代的机会较少，概率为GGAP；对个体配对，按概率Pc进行交叉操作，按概率Pm进行变异操作，交叉操作受γ参数控制；

4）重插入子种群产生新的NIND个个体，计算目前种群适应度函数；

5）判断，是否满足收敛条件，不满足则跳转到步骤2），满足则输出最优解。

4 结果及分析

在80×80空间内布置25个信标节点，15个未知节点，取个体数目为45个，遗传迭代次数为25次，代沟取0.9，变异概率取0.2，交叉概率取0.7。采用主频为3G的计算机在matlab7.0.1环境下进行仿真。

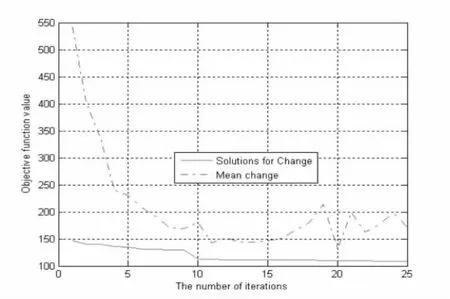
图3 均值和最佳解Fig.3 Average and the best solution

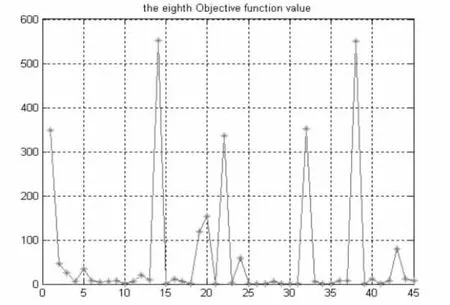
图4 进化到第八代的目标函数值Fig.4 The values of objective function in eighth generation

观察图3和图4，可以看出，均值在不断的变小，表明在不断寻优过程中，解不断向最佳情况变化，采用泰勒级数能够逼近最优解。

为进一步研究参数对结果的影响，分别改变变异概率以及交叉概率。

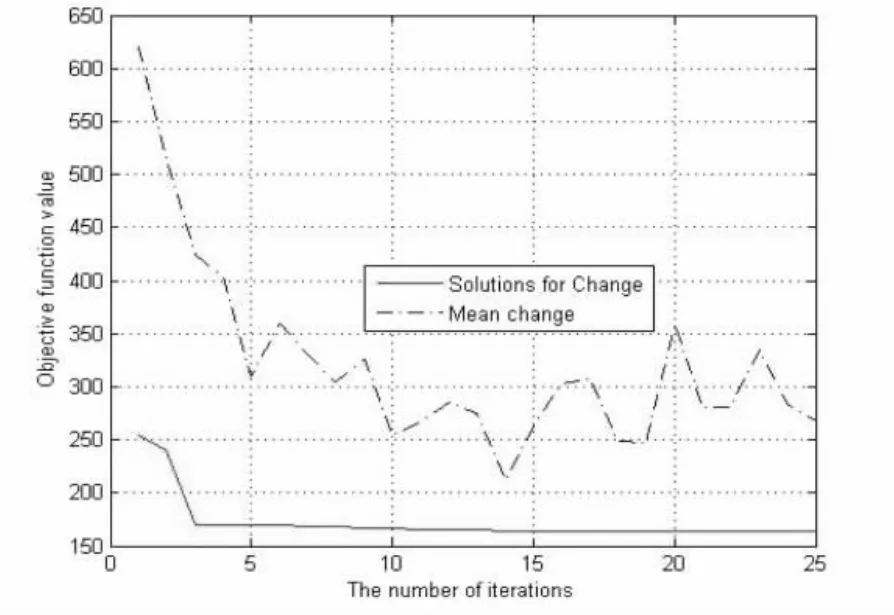
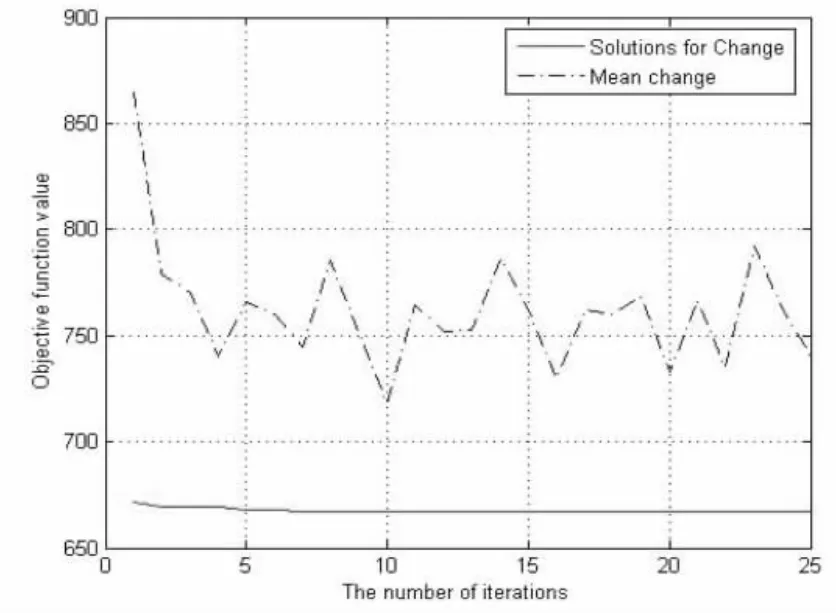
图6 均值和最佳解Fig.6 Average and the best solution

图5和图6是在代沟不变的情况下，分别改变变异和交叉概率得到的，其中图5的变异和交叉概率分别是0.1和0.5，图6的分别是0.01和0.1，对比图3、图5和图6可以看出，图6最佳解几乎没有什么变化，也就是说在变异概率和交叉概率很小的情况下，很难寻找到最优解，从而使得节点定位的精度变低。从以上各图可以得出，采用泰勒级数开展方式，并用遗传算法进行寻优迭代，能够求出最佳解，进而能够对未知节点进行定位。

遗传算法本身只对适应度函数感兴趣，对定位的研究提炼成适应度函数以后，没有再考虑节点实际情况，本文的最佳目标函数解是0，从理论上表明遗传算法能够对节点定位起到优化作用，但到实际应用中去，还有一些工作要做，这也是下一步研究的方向。

5 结束语

水声传感器网络是海洋战略中重要的一环，节点自定位则是水声传感器网络节点自定位的关键技术之一。本文采用泰勒级数对节点间的距离公式进行逼近求解，并用遗传算法对其进行优化，仿真结果表明，在不额外增加硬件设备的条件下，不考虑信标节点与未知节点的通信距离约束情况，能够实现对未知节点的定位误差的寻优求解。

[1]孙利民,李建中,陈 渝,等.无线传感器网络[M].北京:清华大学出版社,2005.

[2]SHENG Xiao-hong,HU Yu-hen.Maximum likelihood multiple-source localization using acoustic energy measurements with wireless sensor networks[J].IEEE Transactions on Signal Processing,2005,53(1):44-53.

[3]HE Tian,HUANG Cheng-du,BLUM B M,et al.Range-Free Localization Schemes in Large Scale Sensor Networks[C]//Proceedings of the 9th Annual Inter2 National Conference on Mobile Computing and Networking (MobiCom).San Diego,California,USA:ACM Press,2003:81-95.

[4]AKYILDIZ I F,POMPILI D,MELODIA T.Underwater acoustic sensor networks:research challenges[J].Ad Hoc Networks,2005,3(3):257-279.

[5]石琴琴.无线传感器网络节点自定位系统及其算法研究[D].上海:上海交通大学,2009.

[6]王驭风,王 岩.基于矢量的无线传感器网络节点定位综合算法[J].通信学报,2008,29(11):227-231.

[7]曹正文,赵 健,高宝建.基于加权最小二乘法的红外多站定位的研究[J].光子学报,2005,34(7):1 001-1 004.

[8]CHENG W,TEYMORIAN A Y,MA L,et al.Underwater localization in sparse 3d acoustic sensor networks 2008.IEEE.

[9]王 怿.水下传感网时钟同步与节点定位研究[D].武汉:华中科技大学,2009.

[10]AKYILDIZ I F,POMPILI D,MELODIA T.Challenges for efficient communication in underwater acoustic sensor networks[J].ACM Sigbed Review,2004,1(2):3-8.

[11]NICULESCU D.Positioning in ad hoc sensor networks.Network[J].IEEE,2004,18(4):24-29.

[12]CUI J H,KONG J,GERLA M,ET AL.The challenges of building scalable mobile underwater wireless sensor networks for aquatic applications[J]..IEEE NETWORK,2006,20(3):12.