巴斯噶蜗线型齿轮的啮合特性及数字制造技术研究

刘永平 孟鹏飞

（①兰州理工大学数字制造技术与应用省部共建教育部重点实验室，甘肃兰州 730050;②兰州理工大学机电工程学院，甘肃兰州 730050）

巴斯噶蜗线是法国数学家为解决阿基米德斜向问题而发明的一种蚌线，这种蜗线在机器中具有独特的作用，通常作为特定场合使用的凸轮轮廓曲线。巴斯噶蜗线型齿轮就是根据上述背景提出的，是一种新型的非圆齿轮，即变传动比齿轮，它以巴斯噶蜗线作为齿轮的节曲线参数方程［1］。

文献［1］的初步研究结果表明，巴斯噶蜗线型齿轮是可以实现变传动比的。这种齿轮可用于在机床往复运动机构、农用机械（谷物收割机、插秧机分插机构）、纺织机械引纬机构、冶金行业连铸机等装置中，实现周期性往复运动［2］;另外，根据巴斯噶蜗线的运动特性，这种蜗线型齿轮还可以用于设计微冲击振动的无曲轴发动机和压缩机，具有传动效率高、运动平稳、工作可靠等优点。

据国内外相关资料来看［2－4］，有关巴斯噶蜗线型齿轮及其共轭的非圆齿轮的研究，目前仅局限于简单的理论分析和计算模拟。本文通过对巴斯噶蜗线型齿轮及其共轭的非圆齿轮的啮合特性及数字制造技术研究，为这类齿轮的设计、制造、测量及应用提供较为系统的理论基础，以进一步拓展非圆齿轮的研究和应用范围。

1 巴斯噶蜗线的定义及性质

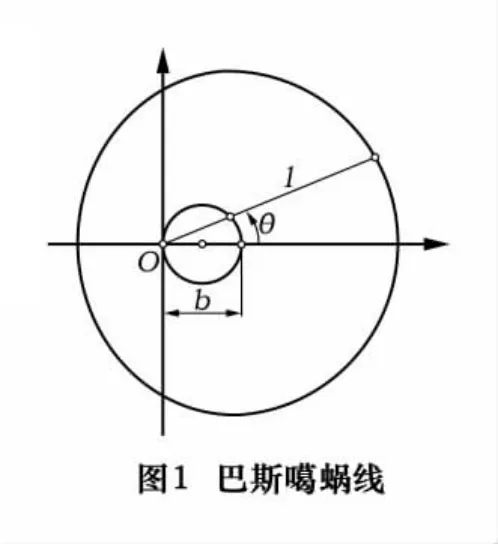
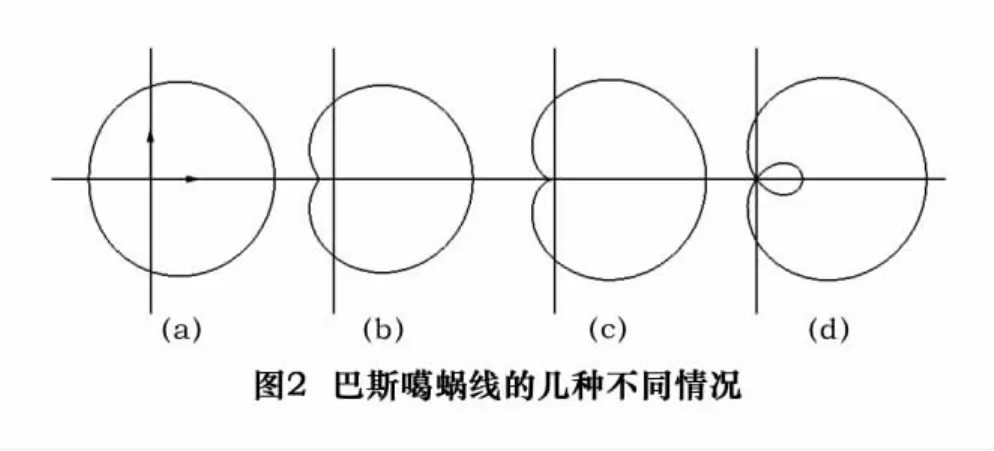
如图1所示，在极坐标系中，半径为b/2、圆心为（b/2，0）的发生圆上任一点的向径方向上，与该点距离为l的点的轨迹称为巴斯噶蜗线［5］。其数学方程为r=bcosθ+l，式中，b为发生圆的直径，l为定长。当b和l的取值不同时，巴斯噶蜗线的形状也不同，主要有以下4种情况，如图2所示:

（1）当 l≥2b 时，Pascal蜗线为全凸封闭节曲线，如图2a所示;

（2）当 b＜l＜2b时，Pascal蜗线为无卷曲的内凹曲线，如图2b所示;

（3）当 l=b时，Pascal蜗线为心脏曲线，如图2c所示;

（4）当l＜b时，Pascal蜗线为有卷曲的内凹曲线，如图2d所示。

2 巴斯噶蜗线型齿轮的节曲线

2．1 巴斯噶蜗线型齿轮副的节曲线方程

对外啮合传动的非圆齿轮副，若主动轮1的节曲线是一巴斯噶蜗线，则该节曲线方程为［1］

根据微分几何，它上面各点的曲率半径计算公式为

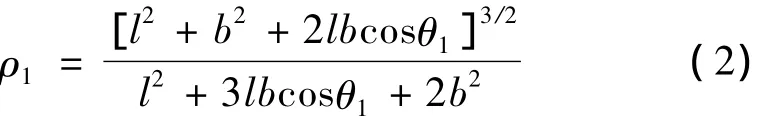
设与其共轭的从动轮2的阶数为n2，则齿轮2节曲线封闭的条件为

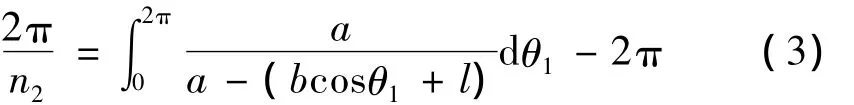
此时齿轮副的中心距a为

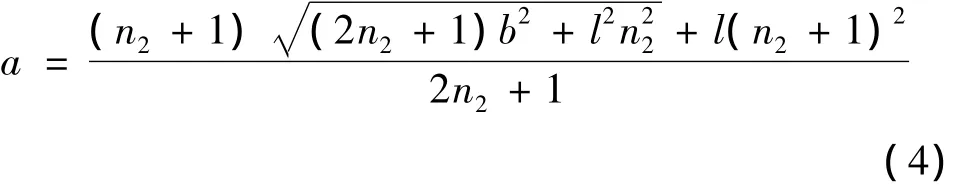
则从动轮2的节曲线方程为

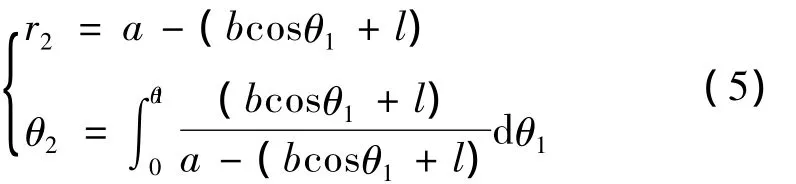
外啮合齿轮副的传动比为

主动轮1的节曲线弧长为

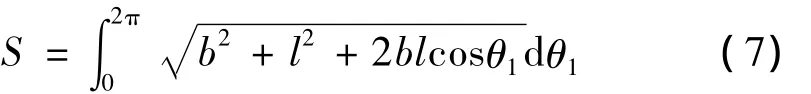
为方便计算，令 L=l+b，Sa=l－ b，k=Sa/L。L称为长轴，Sa称为短轴，k为长短轴比率。则l=（L+Sa）/2，b=（L－Sa）/2。将其转换在直角坐标系中，计算弧长，可得

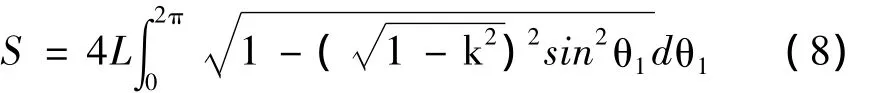
另外，根据节曲线的封闭性和轮齿在节曲线上的均布性，其弧长还必须满足条件［6－8］

因此，在设计这种齿轮时，当主动轮齿数z1、模数m、长短轴比率k确定后，就可以根据式（8）和（9）求解出L的值，得出其主动轮节曲线方程。然后由式（5）得出从动轮节曲线方程。

2．2 巴斯噶蜗线型齿轮的传动比

当 n2=1，k=0、0．2、1/3、2/3、1、1．5、2 时，由公式（5）和（6）计算并绘制蜗线齿轮副传动比曲线，如图3所示。考虑到蜗线节曲线全凸的条件:k≥1/3。从图中可以看出，在k=0时，蜗线是心脏线，其节曲线存在内凹且有尖点，传动比曲线变化幅度较大;当0＜k＜1时，传动比的幅度（Ai12）随着k值的变大而变小，即Ai12和i12成反比;当k=1时，蜗线节曲线变为圆，传动比为一定值;当k＞1时，传动比的幅度（Ai12）随着k值的变大而变大，即Ai12和i12成正比。

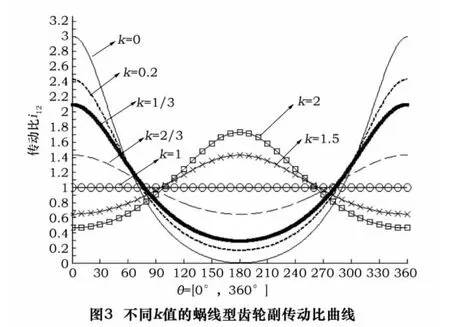
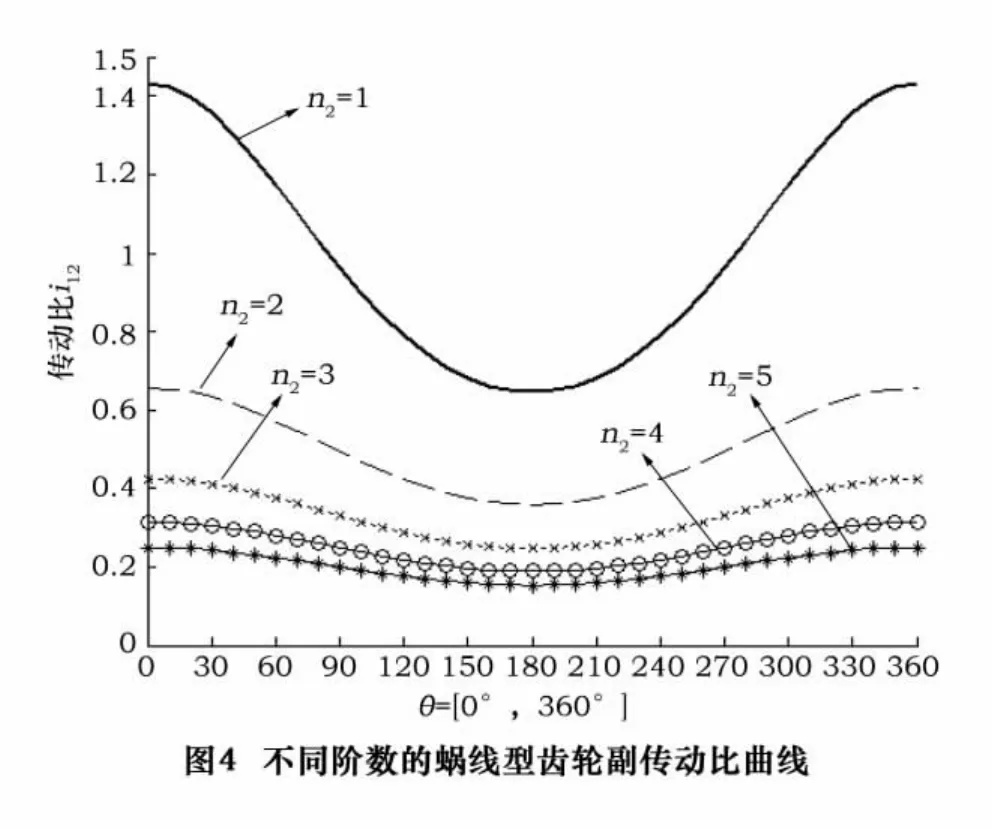
当 k=2/3，n2=1、2、3、4、5 时，蜗线齿轮副的传动比函数曲线如图4所示。可以看出，当k为定值时，传动比的幅度（Ai12）随着n2值的变大而变小，即Ai12和i12成反比。

2．3 巴斯噶蜗线型齿轮的凸凹性

由第1节分析可知，对于这种类型的齿轮，其节曲线的凸凹性和k值有关。当k≥1/3时，该齿轮的节曲线全凸;特别的，当k=1时，蜗线成为半径为l的圆;当0＜k＜1/3时存在内凹但无卷曲;当k=0时，蜗线成为心脏线;当k＜0时，出现卷曲，这种情况无法满足齿轮的传动要求。下面讨论一下与其相啮合的从动轮的凸凹性。

为了计算方便，引入新的符号d。d称为相对中心距。

令ε为偏心率，则

由此可得

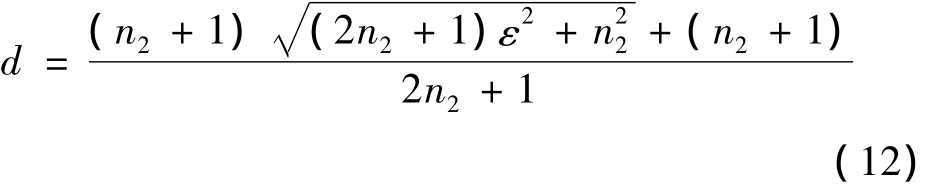
由文献［3］可知，从动轮的曲率半径为

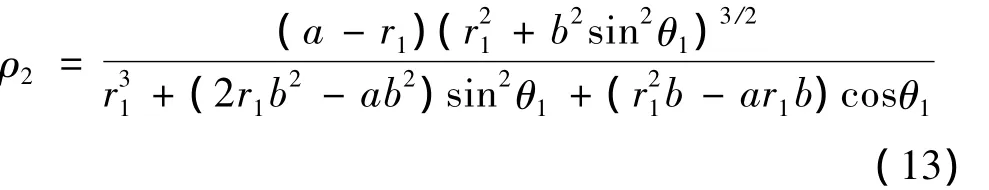
由于a＞r1，式（13）中分子总是正值，所以与蜗线齿轮啮合的非圆齿轮2的节曲线上不出现内凹部分的条件，是分母大于等于零，即

对式（14）求导可知，此式最小值是在θ1=0，r1=l+b时取得，将其代入式（14）得

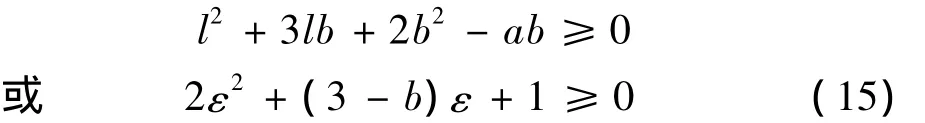
由式（12）及（15）知，当 n2=1、2、3、4 时，k≥1/3就能保证与蜗线齿轮共轭的非圆齿轮节曲线为凸。

3 巴斯噶蜗线型齿轮的齿形设计

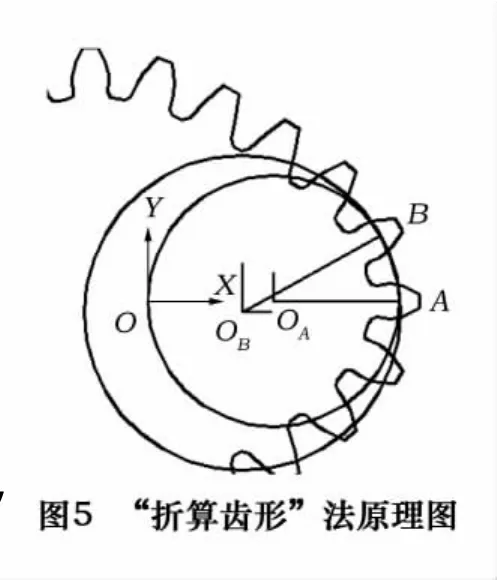
由于非圆齿轮的齿形随着轮齿所处的节曲线位置不同而不同。因此，不论是用齿形法或用解析法来求齿形均较麻烦。为了作图简便，可利用“折算齿形”来绘制［9］。如图5所示，若非圆齿轮上A点是第一个轮齿的中点，该齿的对称轴与A点节曲线的法线方向一致，则该齿的齿形近似于半径为ρA（节曲线上A点的曲率半径）的圆柱齿轮齿形，而该圆柱齿轮的齿数ZA称为“折算齿数”。

折算齿数按如下公式计算

其中，A点的曲率半径即ρA为

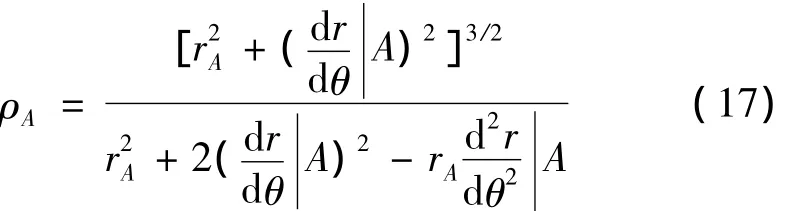
同理可计算出B点以及其他等分点处的曲率半径，并用与其相对应的圆柱齿轮齿廓来代替该等分点处的齿廓。

4 巴斯噶蜗线型齿轮的CAM实例分析

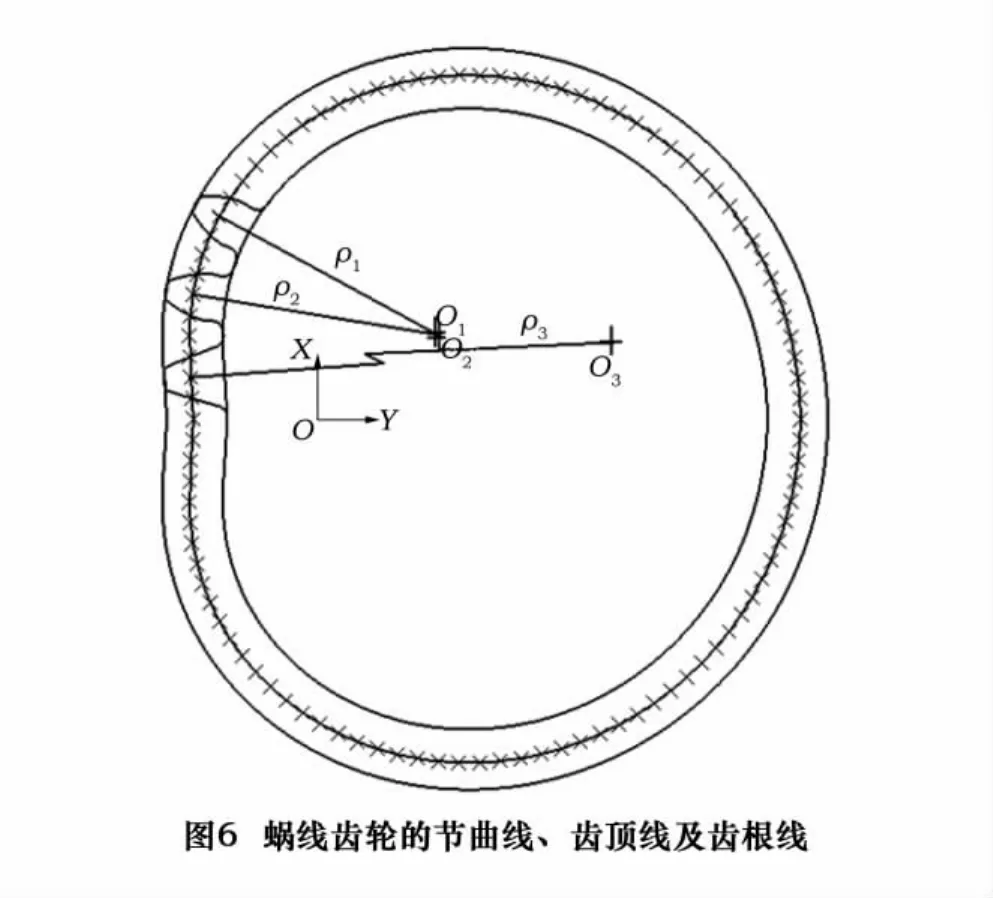
为了验证上述研究内容的正确性，下面列举实例对巴斯噶蜗线型齿轮及其CAM技术进行分析。设给定初始参数:b=20 mm、l=34 mm、m=3 mm、z1=25、n1=1、n2=2。由于l≤2b，故主动轮节曲线不是全凸的，存在一定的内凹。其节曲线、齿顶线、齿根线如图6所示。该齿轮各个等分点处的曲率半径ρ和折算齿数ZA如表1所示。

表1 主动轮齿形参数

根据表1数据，利用CAXA软件绘制出主动轮的各个轮齿齿形，如图7a所示;其三维仿真结果如图7b所示。

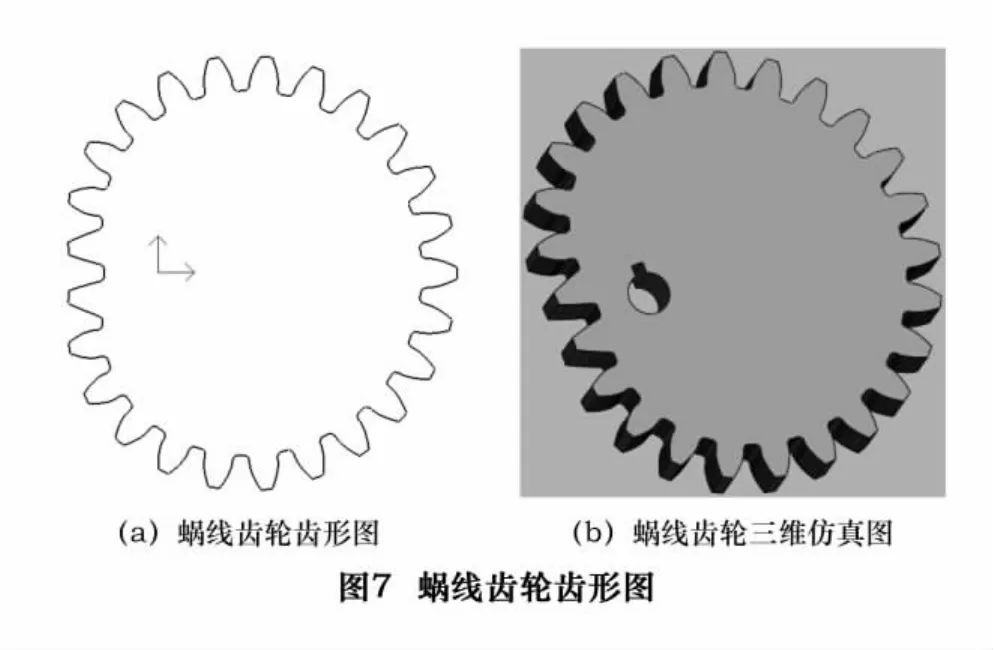
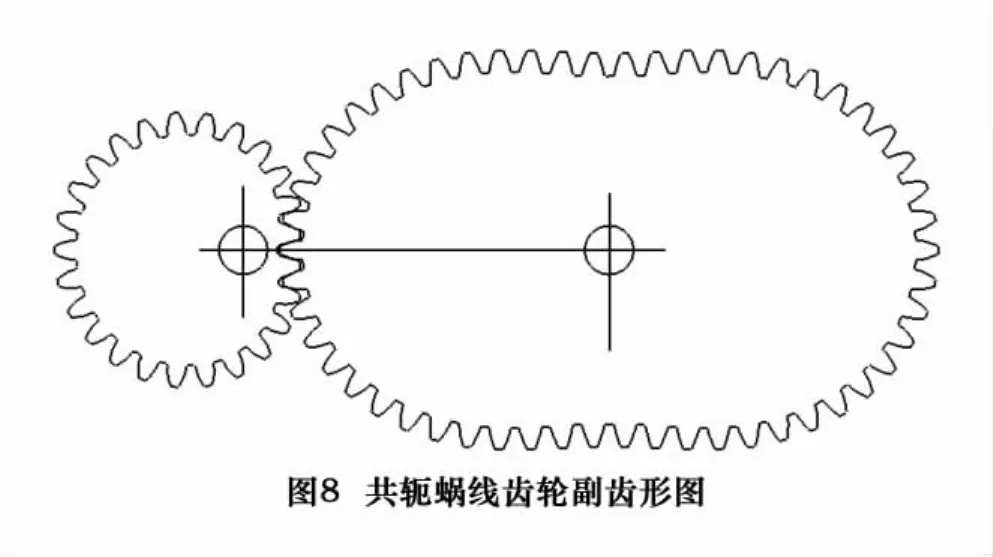
同理，可以计算并绘制出与蜗线齿轮共轭啮合的从动轮，其中z2=54，齿轮副中心距a=110.031 mm，齿轮副啮合状态及齿形图如图8所示。可以看出，从动轮也是一非圆齿轮。

5 结语

巴斯噶蜗线型齿轮是一种新型的非圆齿轮传动机构，具有与传统非圆齿轮（椭圆齿轮、偏心圆齿轮）不可替代的传动特性。本文根据非圆齿轮啮合原理，通过对巴斯噶蜗线型齿轮节曲线的参数化设计、传动特性分析、齿形设计、CAM分析及加工仿真，系统研究了这类齿轮的啮合特性及数字制造技术，验证了这类齿轮传动的可行性及可加工性，为其实际应用提供了较为系统的理论基础，具有较高的实用价值。

［1］刘永平，吴序堂，李鹤岐．常见的凸封闭节曲线非圆齿轮副设计［J］．农业机械学报，2007，38（6）:143 －146．

［2］廖伟，赵匀，方明辉．巴斯噶蜗线齿轮在分插机构上的应用和参数优化［J］．浙江理工大学学报，2009，26（3）:547 －550．

［3］任廷志，程爱明，景奉儒．蜗线齿轮及其共轭齿轮的几何分析与仿真［J］．机械工程学报，2006，42（9）:71－77．

［4］BAIR B W．Computer aided design of non－standard elliptical gear drives［J］．Proceedings of the Institution of Mechanical Engineers，2002，216（4）:473－483．

［5］《数学手册》编写组．数学手册［M］．北京:人民教育出版社，1979．

［6］吴序堂，王贵海．非圆齿轮及非匀速比传动［M］．北京:机械工业出版社，1997．

［7］TONG S H，YANG C H．Generation of identical noncircular pitch curves［J］．Transactions of the ASME，Journal of Mechanical Design，1998，120（2）:337－341．

［8］BAIR B W．Computer aided design of elliptical gears［J］．Transactions of the ASME，Journal of Mechanical Design，2002，124（6）:787－793．

［9］LITVIN F L．Gear geometry and applied theory［M］．NJ:Prentice－Hall，1994．