基于PCA方法的地理系统分析

李旭军

（安徽经济管理学院 计算机工程系，安徽 合肥 230031）

基于PCA方法的地理系统分析

李旭军

（安徽经济管理学院 计算机工程系，安徽 合肥 230031）

在多要素复杂系统的分析，利用主成分分析方法，用较少的变量代替原来较多的变量，可以简化问题的处理，提高处理的效率.

复杂系统；主成分分析法；地理系统

地理环境是多要素复杂系统，进行地理系统分析时，多变量问题是经常会遇到的.变量太多，无疑会增加分析问题的难度与复杂性，而且在许多实际问题中，多个变量之间是具有一定的相关关系的.在各个变量之间相关关系研究的基础上，用较少的新变量代替原来较多的变量，而且使这些较少的新变量尽可能多地保留原来较多的变量所反映的信息.主成分分析把原来多个变量化为少数几个综合指标的一种统计分析方法，是一种降维处理技术[1-3].

1 主成分分析方法原理

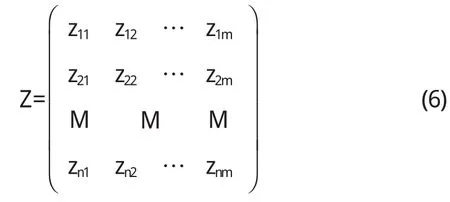
假设有n个地理样本，每个样本共有p个变量描述，这样就构成了一个n×p阶的地理数据矩阵：

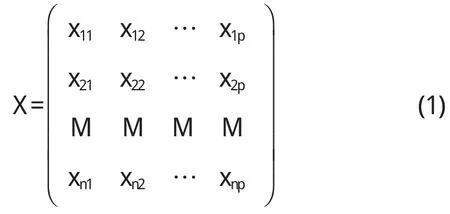
如何从这么多变量的数据中抓住地理事物的内在规律性呢？要解决这一问题，自然要在p维空间中加以考察，这是比较麻烦的.为了克服这一困难，就需要进行降维处理，即用较少的几个综合指标来代替原来较多的变量指标，而且使这些较少的综合指标既能尽量多地反映原来较多指标所反映的信息，同时它们之间又是彼此独立的.那么，这些综合指标（即新变量）应如何选取呢？显然，其最简单的形式就是取原来变量指标的线性组合，适当调整组合系数，使新的变量指标之间相互独立且代表性最好[4-5].

如果记原来的变量指标为x1，x2，…，xp，它们的综合指标——新变量指标为x1，x2，…，xm（m≤p）.则

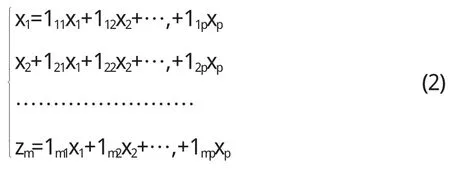
在（2）式中，系数lij由下列原则来决定：

（1）zi与zj（i≠j；i，j=1，2，…，m）相互无关；

（2）z1是x1，x2，…，xp的一切线性组合中方差最大者；z2是与z1不相关的x1，x2，…，xp的所有线性组合中方差最大者；……；zm是与z1，z2，……zm-1都不相关的x1，x2，…，xp的所有线性组合中方差最大者.

这样决定的新变量指标z1，z2，…，zm分别称为原变量指标x1，x2，…，xp的第一，第二，…，第m主成分.其中，z1在总方差中占的比例最大，z2，z3，…，zm的方差依次递减.在实际问题的分析中，常挑选前几个最大的主成分，这样既减少了变量的数目，又抓住了主要矛盾，简化了变量之间的关系.

从以上分析可以看出，找主成分就是确定原来变量xj（j=1，2，…，p）在诸主成分zi（i=1，2，…，m）上的载荷lij（i=1，2，…，m；j=1，2，…，p），从数学上容易知道，它们分别是x1，x2，…，xp的相关矩阵的m个较大的特征值所对应的特征向量.

2 主成分分析的解法

主成分分析的计算步骤

通过上述主成分分析的基本原理的介绍，我们可以把主成分分析计算步骤归纳如下：

（1）计算相关系数矩阵

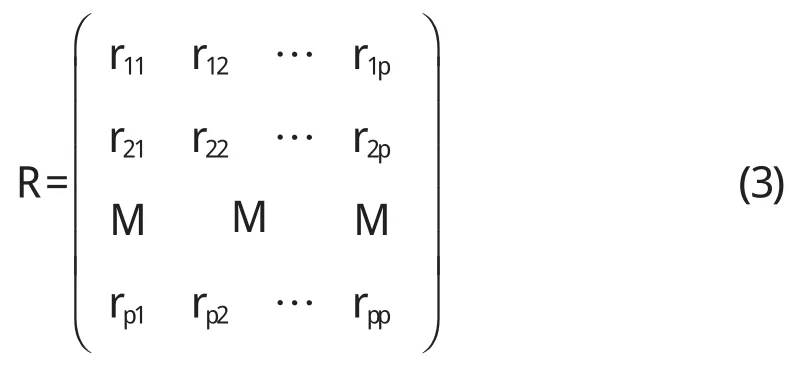
在公式（3）中，rij（i，j=1，2，…，p）为原来变量xi与xj的相关系数，其计算公式为

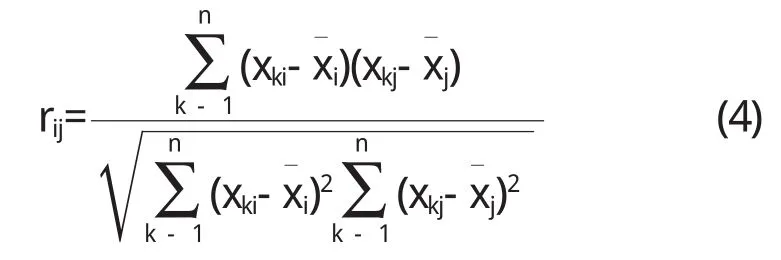
因为R是实对称矩阵（即rij=rji），所以只需计算其上三角元素或下三角元素即可.

（2）计算特征值与特征向量

首先解特征方程|λI-R|=0求出特征值λi（i=1，2，…，p），并使其按大小顺序排列，即λ1≥λ2≥…，≥λp≥0；然后分别求出对应于特征值λi的特征向量ei（i=1，2，…，p）.

（3）计算主成分贡献率及累计贡献率

一般取累计贡献率达85-95％的特征值λ1，λ2，…，λm所对应的第一，第二，……，第m（m≤p）个主成分.

（4）计算主成分载荷

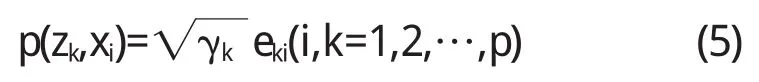
由此可以进一步计算主成分得分：

3 主成分分析法在地理系统分析中的应用

对于某区域地貌-水文系统，其57个流域盆地的九项地理要素：x1为流域盆地总高度（m），x2为流域盆地山口的海拔高度（m），x3为流域盆地周长（m），x4为河道总长度（km），x5为河道总数，x6为平均分叉率，x7为河谷最大坡度（度），x8为河源数，x9为流域盆地面积（km2）.

1、首先对原始数据作标准化处理，由公式（4）计算得相关系数矩阵（见表1）.

表1 相关系数矩阵

2、由相关系数矩阵计算特征值，以及各个主成分的贡献率与累计贡献率（见表2）.由表2-16可知，第一，第二，第三主成分的累计贡献率已高达86.5％，故只需求出第一，第二，第三主成分z1，z2，z3即可.

（3）对于特征值 λ1=5.043，λ2=1.746，λ3=0.997分别求出其特征向量e1，e2，e3，并计算各变量x1，x2，……，x9在各主成分上的载荷得到主成分载荷矩阵（见表3）.

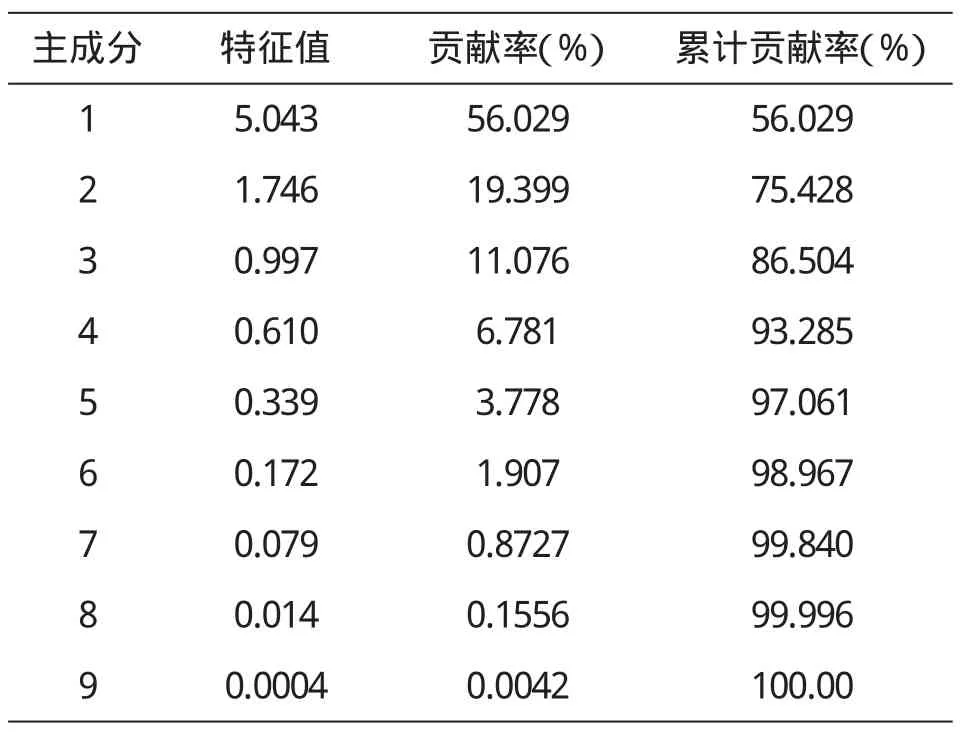
表2 特征值及主成分贡献率

表3 主成分载荷矩阵

从表3可以看出，第一主成分z1与x1，x3，x4，x5，x8，x9有较大的正相关，这是由于这六个地理要素与流域盆地的规模有关，因此第一主成分可以被认为是流域盆地规模的代表：第二主成分z2与x2有较大的正相关，与x7有较大的负相关，而这两个地理要素是与流域切割程度有关的，因此第二主成分可以被认为是流域侵蚀状况的代表；第三主成分z3与x6有较大的正相关，而地理要素x6是流域比较独立的特性——河系形态的表征，因此，第三主成成可以被认为是代表河系形态的主成分.

4 结论

以上分析结果表明，根据主成分载荷，该区域地貌-水文系统的九项地理要素可以被归为三类，即流域盆地的规模，流域侵蚀状况和流域河系形态.如果选取其中相关系数绝对值最大者作为代表，则流域面积，流域盆地出口的海拔高度和分叉率可作为这三类地理要素的代表，利用这三个要素代替原来九个要素进行区域地貌-水文系统分析，可以使问题大大地简化.

〔1〕张科静.基于主成分分析法的城市创意竞争力评价[J].情报杂志，2010,29（4）:68-71.

〔2〕田盈.基于加权主成分分析的企业技术创新绩效评价模型研究[J].科技进步与对策,2008,25（3）:130-133.

〔3〕张洪波.主成分分析法与概率神经网络在模拟电路故障诊断中的应用[J].计算机测量与控制,2008,16（12）:1789-1792.

〔4〕杨海澜.主成分分析结合神经网络技术在焊接质量控制中的应用[J].焊接学报,2003,24（4）:55-60.

〔5〕李晓刚.基于主成分回归的公路客运量预测模型研究[J].交通标准化,2009,（156）:187-191.

P208

A

1673-260X（2011）12-0041-03