基于图像融合的电容成像*

李守晓，王化祥，崔自强，薛 倩

(天津大学电气与自动化工程学院，天津 300072)

电容成像技术(Electrical Capacitance Tomography)是80年代初由西方国家开始研究开发［1］。作为一种非侵入式的流动参数可视化检测技术，被认为是极具发展前景的过程成像技术［2］。目前，电容层析成像系统已在流化床内物料分布、油/气两相流系统、气力输送的气/固两相流等流型可视化监测中得到应用。

目前广泛应用的ECT成像算法包括非迭代算法和迭代算法［3］。非迭代算法包括线性反投影(LBP)、Tikhonov正则化算法、基于截断奇异值分解的直接算法(SVD);迭代算法包括Landweber迭代算法、牛顿－拉夫逊迭代算法以及共轭梯度迭代算法(CG)。线性反投影算法虽简单快速，但该算法成像质量较差。Landweber迭代算法与最速梯度下降法类似，但其收敛性比较差［4］。由于迭代算法与非迭代算法所成图像具有较多差异，所以本文分别从迭代算法和非迭代算法任意选一种算法进行小波图像融合，提高图像质量。

1 ECT系统基本理论

电容层析成像系统主要包括三个部分:传感器部分(阵电极电容系统)、数据采集部分、图像重建计算机部分，如图1所示［5］。传感器部分由安装在绝缘管道外壁的阵列电极组成。数据采集部分测量任意一对电极间的电容值，将采集到的电容值传到图像重建计算机，运用图像重建算法进行图像重建。

图1 电容层析系统原理图

在ECT系统中，测量电极获得的电容值与被测场域的介电常数分布为非线性关系。当场域有足够多的剖分单元，非线性关系可以近似为线性，用矩阵形式表示

式中:A为灵敏度矩阵;ρ为电容向量;δ为介电常数的向量，即灰度值。

2 基于小波图像融合的电容成像算法

图像融合是将不同传感器得到的多个图像根据一定算法进行综合处理，以得到一个新的、满足某种需求的新图像，它可将同一对象的两个或者更多的图像合成在一幅图像中，以使它比原来的任何一幅图像更满足人们的要求［6］。本文基于小波变换的图像融合方法具有完善的重构能力，使信号在分解过程中没有信息损失和冗余信息;容易提取原始图像的结构信息和细节信息，把图像分解成平均图像和细节图像的组合，分别代表了图像的不同结构。利用这些特性可以获得更佳的图像。

2.1 小波变换

设任意的函数f(t)∈L2(R)，则其连续小波变换［7］为

其中，a为伸缩因子，b为平移因子。其重构公式为

电阻层析成像得到的重建图像多为二维，因此需对图像进行二维小波变换，其一般形式可表示为

小波函数ψ(t)是由尺度函数φ(t)的伸缩和平移的线性组合生成的，而尺度函数φ(t)满足两尺度差分方程，它们关系如下:

其中，g为高通滤波器，h为低通滤波器，g和h为正交镜像滤波器，存在如下关系:

2.2 小波图像融合算法

基于小波图像融合［8］算法如下:

(1)基于电磁场有限元仿真软件COMSOL建立传感器仿真模型，并以共轭梯度算法和奇异值分解算法进行成像;

(2)对用CG及SVD算法重构的图像分别进行二维小波变换，建立图像的小波塔形分解;

(3)对两幅图像的分解层分别进行融合处理。各分解层上的不同频率分量采用不同的融合算子进行融合，最后得到融合后的小波金字塔;

(4)对融合后的小波金字塔进行小波重构，最后得到的重构图像即为融合图像。

图2 小波图像融合

显然，融合规则及融合算子的选择是非常重要的，直接关系图像融合质量。为了获得更好的融合效果，结合电阻层析成像中出现伪迹以及边缘与中心区域成像模糊的特点，本文采用的融合规则及融合算子如下:

①对分解后的低频部分，采用加权平均的融合规则，如下式所示，∂为权重系数，本文取∂=0.5。la(x，y)由CG算法所成像的低频部分的数据值;lb(x，y)由SVD算法所成像的低频部分的数据值。该规则具有消除部分噪声，原图像信息损失较少，抑制伪像。

②对于分解后高频部分，采用取绝对值较大的融合规则。如下式所示，ha(x，y)由CG算法所成像的高频部分的数据值;hb(x，y)由SVD算法所成像的高频部分的数据值。小波分解中，绝对值较大的小波高频系数对应着亮度急剧变化的点，即为图像中对比度变换较大的边缘特征。该规则可以使成像区域中变化大的区域和边界清晰化。

3 实验与仿真结果分析

为了验证基于小波图像融合方法的有效性，采用ECT仿真及实验方法对基于CG、SVD和小波图像融合方法三种图像重建算法的图像质量进行比较。

3.1 ECT 仿真结果

在油/气两相流仿真实验中，采用12电极敏感阵列。本文采用电磁场有限元仿真软件COMSOL和MATLAB对ECT图像重建算法进行仿真评价。用有限元仿真软件COMSOL建立ECT传感器模型［12］如图3所示。图像重建计算机配置为Pentium 4－2.67GHz的 CPU，1.5 GB 的内存，支持 OpenGL，显存为512M，Windows 7的操作系统。正问题采用COMSOL自动网格剖分，剖分单元采用三角单元如图3(a);图像重建采用3228个正方体单元进行计算，如图3(b)。

图3

基于COMSOL对12电极ECT进行仿真。仿真模型如图4所示，其中，ECT场域内白色部分为空气，其介电常数为1;黑色部分模拟有机玻璃，其介电常数为2.7。用COMSOL对仿真模型进行有限元剖分，有限元单元［13］采用三角单元如图4所示。模型①共有804个节点，1 486个三角单元;模型②共有763个节点，1 404个三角单元;模型③共有880个节点，1 638个三角单元，模型④共有1 031个节点，1 940个三角单元;模型⑤共有678个节点，1 234个三角单元。

应用MATLAB编程实现共轭梯度和奇异值分解两种图像重建算法，对图4所示的5种模型进行图像重建。然后将所得的图像运用MATLAB程序实现小波融合。实验所得图像采用PNG图像(402×402)，小波基采用Daubechies小波。将小波融合后的图像与共轭梯度算法和奇异值分解算法所成图像进行比较如表1所示。

表1 ECT仿真成像效果图

本文引入原始图像与重建图像的相关系数［9］

式中，δ*是被测区域内的真实介电常数分布;δ是介电常数计算值;和分别是δ*和δ的平均值。图像相关系数表明原始分布和重建分布之间的空间相似性，该值越大说明图像重建质量越好。

定义图像相对误差［10］如下:

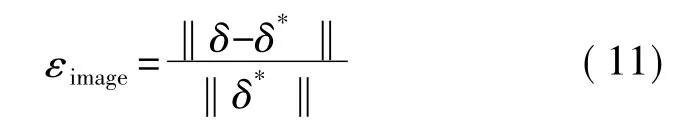
图像相对误差越小，说明所成图像更接近真实值。对仿真所得图像进行评价，如表3所示。

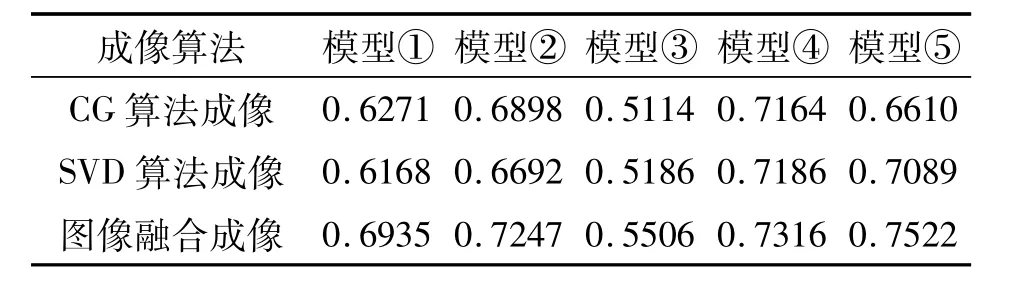
表2 图像相关系数

表3 图像相对误差

模型①为中心流，由表1可以看出，CG方法成像离散相较大，小波图像融合成像中心区域接近真实值。由SVD算法成像连续相不均匀，小波图像融合成像连续相较均匀。通过表2图像相关系数可以看出图像融合成像的图像相关系数较大说明其所成图像更接近真实值。由表3可以看出其图像相对误差也较小。模型③和模型④为两种泡状流，可以看出小波融合后的图像质量更高。综上所述，由表1可以看出经过小波图像融合成像具有之前两幅图像特征，能够更好的反映真实物场分布。由表2和表3可以分别看出小波图像融合成像的图像相关系数比其它两幅图像都高，图像相对误差比其它两幅都低，所以可以说明由小波融合算法得到的图像较CG算法的图像和SVD算法所成图像质量更高。

3.2 ECT 实验结果

电容成像实验系统［11］如图5所示，激励电压为20Vp－p，激励频率范围 10 kHz ～ 1 MHz(实验激励频率为200 kHz)，激励模式为相邻激励，采用相邻测量的测量模式，解调方式为数字相敏解调，测量信噪比60 dB，数据采集速度为1010帧/s，每幅含66个数据，USB2.0数据接口，上位机软件采用VC6.0的界面［12］，运用OpenGL进行图像显示。圆柱形容器的直径为6 cm，12电极尺寸为1.4 cm×7 cm的电极;1m长单层屏蔽电缆。两个实验分别用直径2.5 cm有机玻璃棒，有机玻璃颗粒进行成像，空气的介电常数为1，有机玻璃的介电常数为2.7。

图5 ECT流型成像实验

运用实验装置进行流型实验。实验模拟了二种流型，分别为中心流和层状流，所得结果如表4所示［13］。从图中可以看出，小波图像融合成像结合二者的优点，成像分辨率更高，得到了与原始图像具有更高相似性的图像。

表4 ECT实验成像效果图

4 结语

本文采用COMSOL建立电容层析成像模型进行仿真，任选两种算法成像运用小波融合的方法进行处理，本文选CG算法和SVD算法，结果表明基于小波融合的图像明显好于两种算法得到的图像。然后进行ECT流型实验，采用同样的方法对图像进行处理，实验结果与仿真基本相同。综上所述小波融合的方法对ECT实验和仿真所成图像质量都有提高。

［1］Yang W Q.Editorial.Measurement Science and Technology［M］.2001.12.

［2］Wang Min.Inverse Solutions for Electrical Impedance Tomography Based on Conjugate Gradients Methods［J］.Meas Sci Technol，2002，13(1):101－117.

［3］王化祥，范文茹，胡理.基于GMRES和Tikhonov正则化的生物电阻抗图像重建算法［J］.生物医学工程学杂志，2009，26(4):701－705.

［4］彭黎辉，陆耿.电容成像图像重建算法原理及评价［J］.清华大学学报，2004，44(4):478－484.

［5］张立峰，王化祥.基于SVM及电容层析成像的两相流流型识别［J］.仪器仪表学报，2009，30(4):812－816.

［6］郭雷，李晖晖，鲍永生.图像融合［M］.北京:电子工业出版社，2008.

［7］周伟.Matlab小波分析高级技术［M］.西安电子科技大学出版社.2006.1.

［8］黄靓，黄政宇，汪优.图像融合在混凝土超声波层析成像中的应用研究［J］.计算机应用，2008，28(10):2670－2675.

［9］张立峰，电学层析成像激励测量模式及图像重建算法研究:［博士学位论文］，天津:天津大学，2010.8.

［10］Wang H X，Tang L，Cao Z.An Image Reconstruction Algorithm Based on Total Variation with Adaptive Mesh Refinement for ECT［J］.Flow Measurement and Instrumentation，2007，18:262－267.

［11］张雪辉，王化祥.电容层析成像数字化系统设计［J］.传感技术学报，2007，20(8):1826－1830.

［12］马敏，王化祥，田莉敏.基于DSP的数字化电容层析成像系统［J］.传感技术学报，2006，19(3):705－708.

［13］TSAID-M，HSIAO B.Automatic Surface Inspection Using Wavelet Reconstruction［J］.Pattern Recognition，2001，34(6):1285－1305.