半导体器件模拟方法研究

刘 影 丁红梅

（电子科技大学物理电子学院，四川 成都 610054）

半导体器件模拟方法研究

刘 影 丁红梅

（电子科技大学物理电子学院，四川 成都 610054）

主要介绍了半导体器件模拟中的几种物理模型和三角形网格自适应划分的算法。并以泊松方程为例，介绍了如何在网格中进行方程的离散化，以及后期计算方程组的几种数值方法并比较各种算法的优缺点，同时得到解的示意图。

半导体器件；器件模拟；网格划分；数值计算

自从20世纪60年代以来，半导体器件模拟在集成电路工业中扮演着越来越重要的角色。在半导体集成电路产业设备异常昂贵的今天，以流片试验的方式去验证设计成果，必然导致资源的巨大损耗，因此半导体器件模拟技术就显得尤为重要。同时，随着计算机性能的提高，半导体器件模拟软件开始为更多的人所熟悉。

半导体器件模拟首先要选择物理模型和基本方程。物理模型由漂移扩散模型(DDM)向流体动力学模型(HDM)甚至量子流体动力学模型(QHDM)发展。漂移扩散模型是最经典的模型，这种模型对于微米级的器件精度非常好，但是随着半导体器件尺寸的不断缩小，在进入亚微米和深亚微米以后，很多效应随之产生，流体动力学模型能够很好的模拟这些效应，虽然占用CPU时间比DDM稍有增加，但其精度有了进一步的提高。目前比较流行的商用软件MEDICI、PISCES[1]、ISE等普遍采用了DDM，同时提供了HDM供用户选择。在进入纳米级器件以后，载流子的波动性占主导地位，小尺寸器件的电导有很大的起伏，这时需要用到量子修正的漂移扩散模型(QDDM)，它在经典漂移扩散模型(DDM)的基础之上，添加量子势方程完成对载流子浓度的量子修正。该模型优点是计算难度相对较低，效率较高，能够有效地模拟较为复杂的器件中量子力学效应的影响，但模拟的精度有所降低。[2]

1 基本物理方程

半导体及半导体器件的电特性可由5个基本方程来描述，它们是Poisson方程、电子空穴的输运方程和电子空穴的连续性方程。

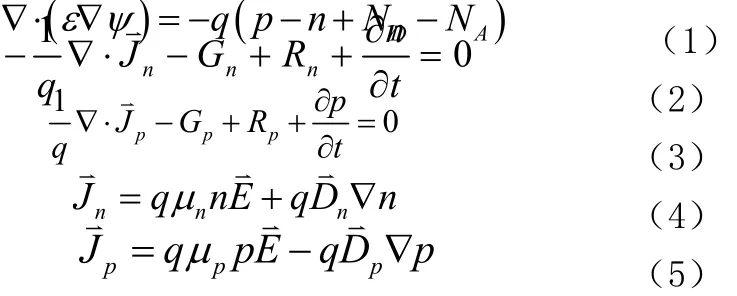
其中E =-▽ψ，Dn= kTμnq 与Dp= kTμpq 为爱因斯坦关系（适用于非简并半导体）。μn 和μp分别为电子和空穴的迁移率。载流子的迁移率一般不是常数，而是与材料，杂质浓度和电场有关[3]。

2 模拟所用网格

得到上述方程组的解析解是很困难的。在工程上一般把方程组在特定的网格上离散化，进行求解得到数值解。半导体器件模拟一般采用矩形网格或者三角网格。矩形网格比较容易实现，而且在矩形网格上离散化形成的方程形式也比较简单。三角形网格实现起来比较复杂，但是能更好的适应复杂器件的几何外形，较之矩形网格，三角网格有以下优点：1）采用三角网格进行局部自适应网格划分时，不会在其他部分引入不必要的节点；2）现代半导体器件的几何外形比较复杂，三角网格更容易覆盖所要模拟的区域[6]。

下面主要介绍三角形网格及其自适应网格划分。首先由用户在输入文件中给出器件的几何外形与边界信息，由网格划分软件得到首次的网格，网格信息中包含着网格节点和网格单元的信息。接下来是网格的自适应划分了，根据输入文件的中的掺杂浓度进行第一次自适应划分，以后每次方程求解之后还可以再次进行自适应划分，得到新的网格后，在新的网格基础上再次求解，一直到方程收敛为止[6]。自适应划分的判据一般有两种：一种方法是根据物理量（电势、电场等）的绝对变化，或者相对变化；另一种是截断误差。这两种方法各有优缺点。第一种方法实现起来比较容易，但是在数学概念上不是很严格。第二种方法需要比较复杂的数学推导，但实现起来比较复杂[8]。

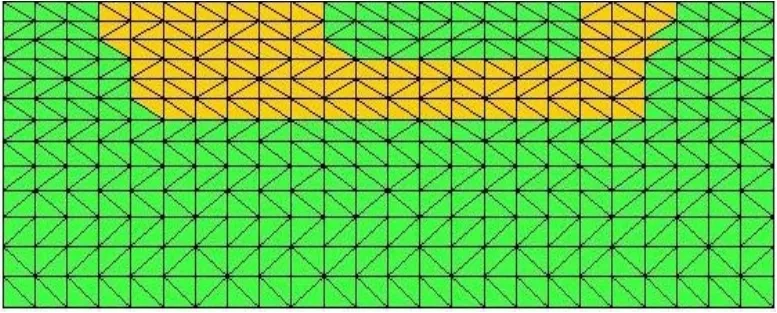
图1 BJT的初始网格[5]

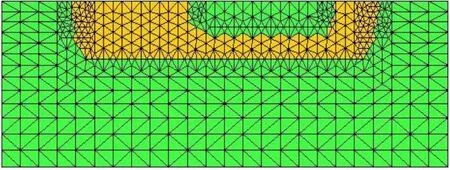
图2 自适应划分后的网格[5]

自适应网格划分的具体实现如图3所示。检查所有的网格节点，如果某些三角形网格单元需要自适应划分，那么这个三角形被分成4个小三角形。第0级的三角形代表初始的网格。自适应划分后形成的4个小三角形称为第一级，同时，用线性插值或者对数插值的方法，在新的网格上重新分配物理量。在所有的第0级网格检查完成之后，接着进行检查第一级的网格。如果第一级的三角元需要自适应划分，那么一个第一级的三角元被分解成第二级的三角元，以此类推，直到所有的三角元都满足要求为止[8]。

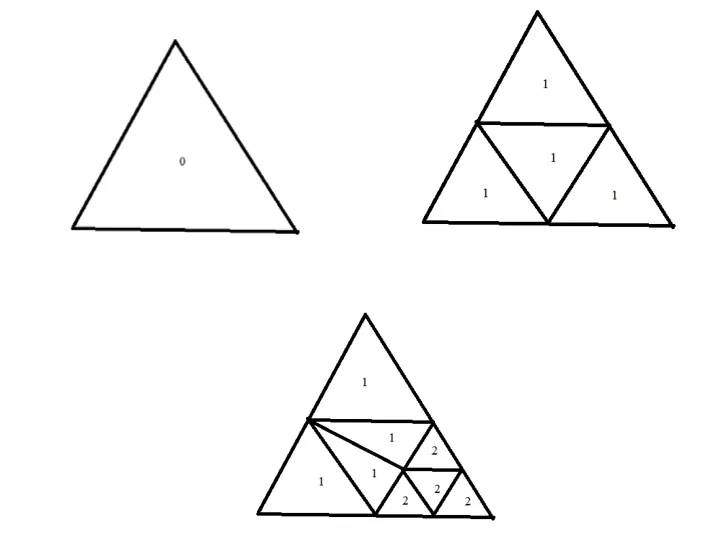
图3 三角形网格自适应划分过程

3 数值方法

我们以2D Poisson方程为例，讨论如何离散化，建立方程组。对于二维一阶泊松方程：[Ke]

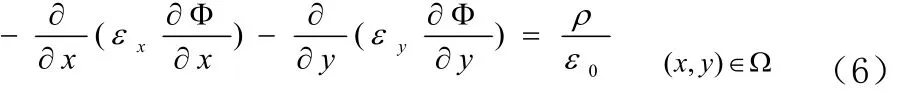
矩阵 的元素为

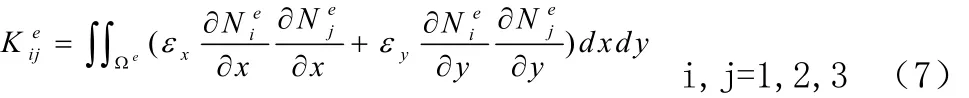
向量{e}b 的元素为：

对于插值函数j=1,2,3

其中插值系数的表达式如下：=第e个单元的面积

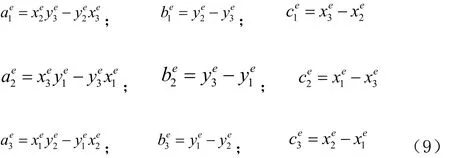
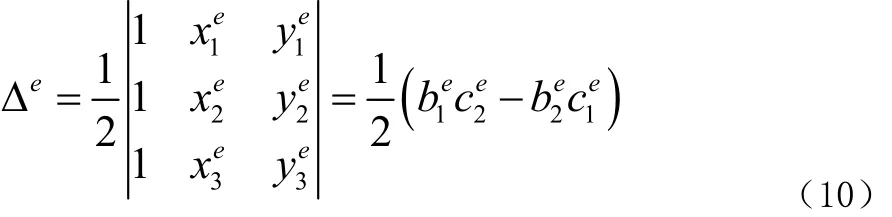
根据基本公式

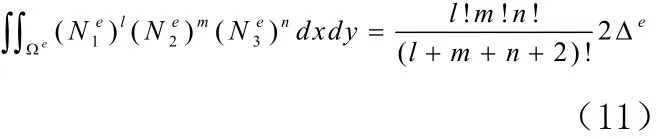
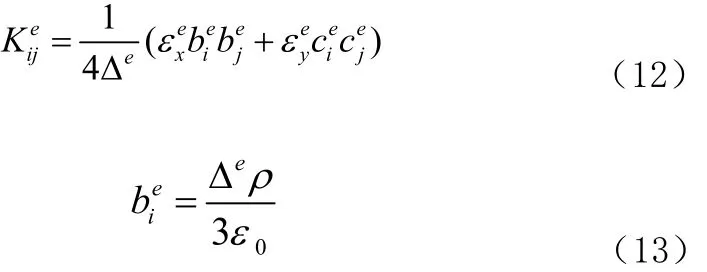
通过上述理论基础模拟BJT。得到了泊松方程的数值解。用Origin仿图[7]，如图4所示：

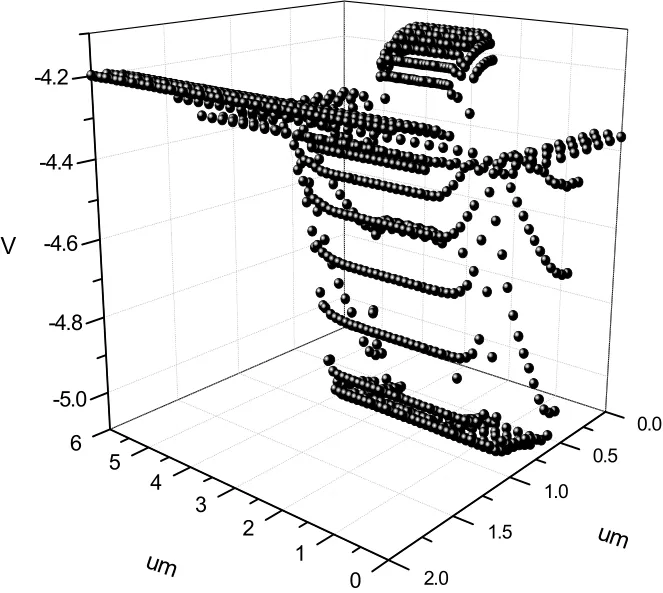
图4 BJT中电势分布图

4 结束语

当今的半导体器件特征尺寸正在按照摩尔定律迅速缩小，这就对器件模拟程序提出了新的要求，而同时在半导体集成电路高速发展的推动下，器件模拟技术也日益趋于完善，功能也越来越强大，器件模拟技术在推动技术发展的时也促进了自身的完善。在未来的技术发展过程中器件模拟技术还将发挥着更重要的作用。

[1] Integrated Circuits Laboratory Stanford University. PISCES 2ET and Its application Subsystem.1994.

[2] 蒲月皎,刘丕均,张亚非,王印月.纳米级MOSFET器件模拟的载流子输运模型[J].固体电子学研究与进展,2005, 25(2).

[3] (日)苍田卫.半导体器件的数值分析[M].张光华,译.电子工业出版社,1985.10.

[4] 刘恩峰,刘晓彦,韩汝琦.半导体器件模拟技术的研究[J].微电子学,2002,32(3).

[5] SILVACO International. ATLAS User’s Manual. Version 5.10.R.December 8,2005.

[6] (美)金建铭.电磁场有限元方法[M].王建国,译.西安:西安电子科技大学出版社,1998.

The Research of Semiconductor Device Simulation

Study of Semiconductor device simulation method are reviewed in the paper. Such as physical models,algorithm of refining mesh, and numerical methods. The discretization of the Poison equation on triangle grids is illustrated. And also describe some numerical methods commonly used for solution of nonlinear equation. And also get the solutions’ diagrammatic sketch.

Semiconductor device; Device simulation; Triangle grid; Numerical method

TN303

A

1008-1151(2011)10-0011-02

2011-07-30

刘影，电子科技大学物理电子学院研究生。