固定摄像头图像中测算目标距离和尺寸的算法

陈大海 莫 林 易向阳

（广西大学计算机与电子工程学院，广西 南宁 530004）

固定摄像头图像中测算目标距离和尺寸的算法

陈大海 莫 林 易向阳

（广西大学计算机与电子工程学院，广西 南宁 530004）

利用简单的几何方法来实现在单目固定镜头条件下获取图像中目标的大小尺寸和目标与摄像机的距离。这种方法简单易用，运算量小，只需要在初次摄像头拍摄画面时设置初始条件，就可以在以后的图像中快速完成目标大小距离等参数的计算。

图像测距；形状特征；图像处理；视频监控

1 引言

在视频监控系统中为了能对目标进行识别分类和行为分析理解等，获取图像中目标的尺寸和目标与摄像机的距离等参数是非常重要的。目标的测距与目标尺寸的测量有直接的联系。目前研究中的和应用中的目标测距方法有很多种，但是这些方法一般都比较繁琐成本比较高。文章使用简单的几何方法来实现在单目固定镜头条件下获取图像中目标的大小尺寸和目标与摄像机的距离。该方法简单易用，运算量小，只需要在初次摄像头拍摄画面时设置初始条件，就可以在以后的图像中快速完成目标大小距离等参数的计算。该方法适用于大多数的室外中远距离监控环境。

2 图像中目标距离的测量方法

目标距离的测量的方法有很多种，目前常用的距离测量方法主要分为两大类：主动方式和被动方式。

主动测距法使用激光等波束或具有一定纹理结构的光照射目标，通过分析物体反射光的纹理形变或测量光束的传播时间来确定物体的距离。另外主动测距方法又可以分为：接触式测距和非接触式测距法两类。

接触式测距法对物体表面进行逐点扫描逐点测量，所以费用高、费时，不适合测量柔软的物体。非接触主动测距法采用微波、声纳测、激光等手段，通过探测波在物体和传感器之间的传播时间来计算物体与传感器之间的距离，该方法比较适合于测量距离较远而精度要求不高的物体。另外非接触主动测距法还可以采用结构光场法，通过测量投射在目标表面的图案形变，采用三角测量原理计算物体距离，测量精度较高。

主动测距方法优点是精确度比较高，缺点是发射各种波可能对目标有伤害或引起测量器材的暴露，设备比较昂贵，测距装置成本与测距装置的分辨率成正比，另外三维立体景物的对焦困难，容易造成图像中目标的模糊现象。

被动测距方法直接通过目标的影像信息来确定物体的距离。被动测距法主要有：立体视觉[1]、运动测距法[2]、单目测距[3]等。

立体视觉是模仿人类的立体感知分析方法将双目或多目摄像头在不同的视点观察同一景物，获取在不同视角下的目标图像拍摄的物体二维图像。通过三角测量原理计算图像像素间的位置偏差即视差来获取景物的三维信息。立体视觉分为图像获取、摄像机定标、特征提取、立体匹配、深度确定及内插等几部分。

运动测距法用单目摄像头在不同时间或不同的空间位置获取连续的目标图像。通过目标在二维图像序列的时间和空间变化计算出目标的距离和其他参数。

运动测距需要在不同图像中寻找对应点。寻找目标的对应特征，并计算出它们之间的偏差量，以此来计算目标的距离和尺寸参数，但是要提取物体的特征比较复杂费时。当目标在所处的场景中有不时被遮挡情况下，可能会出现目标的特征点无法连续被找到使得无法进行距离测算。

单目测距中基于图像处理的测距方法有：对焦测距法和散焦测距法[4]。

对焦测距法 DFF(Depth from Focus)通过调节光学参数拍摄一系列的目标图像，在这些图像中找出目标最清晰的那一张图像，根据这张图像的拍摄参数，利用几何光学的成像原理，计算出目标距离[5,6]。该方法距离的测算精确。这种方法要在不同光学参数下，对物体拍摄一大批的图像，对这些图像进行分析需要比较大的计算量，该方法难于进行实时测量。

散焦测距法 DFD(Depth from Defocus)是一种从离焦的图像中获得物体深度信息的方法[7,8]。根据物体散焦程度越大图像越模糊的原理，利用在不同光学参数下拍摄的两幅或三幅图像来确定散焦点扩散函数的扩散参数，根据散焦扩散参数与物体距离的关系来进行深度计算。

对焦测距法和散焦测距法不需要寻找目标对应特征点，没有了被遮挡无法测量的问题。散焦测距法与对焦测距方法比较起来，它无需拍摄大量图像，操作运算都是对局域图像进行的，且计算方法简单，运算速度快，所以可高密集地测量物体的深度。

上述测量方法的共同特点是测量的精度主要决定于测量仪器，如果要求提高精度，所需的费用会大幅度的增加。在现实生活中，在很多情况下所要求的精度并不高，因此，可以寻找一些费用成本较低而能达到一定精度要求的方法来解决此问题。

3 固定摄像头的单目测距

3.1 应用条件

在大多数的室外视频监控应用领域中，大部分的摄像头都是固定的，而且往往都是中远程的监控场景，定焦摄像机。在这种摄像条件下，只要是非广角拍摄，目标离摄像机比较远时，目标在图像中的变形就会比较小。这就对目标的测距和几何参数的测量提供了比较好的条件。

3.2 视频图像中获取的初步参数

定义目标对象i的实际高度为Hi、实际宽度为Wi。

下面需要将这个像素表示的长宽数据换算出实际大小，计算出这个对象的实际大小并提前计算出两个重要参数：目标距离摄像头的距离和摄像头的拍摄角度。固定摄像头的安装高度在实际安装测试时可以测量得到 a，固定摄像头的拍摄画面的上沿和下沿距离摄像头垂平面的距离b和c也可以实际测量到。

目标在图像上的大小是和目标与摄像头的距离成反比，遵循近大远小的规则，可以通过几何运算公式得到目标实际大小。为了减小计算量可以简化算法，只要摄像头不是变形很大的广角镜头，可以认为目标自身在图像中的长度和宽度是随着目标和摄像头的距离以相同比例变化的。

3.3 视频图像目标参数计算

（1）计算步骤

由于设计条件是固定摄像头下不变焦的监控系统的距离和目标尺寸计算，所以摄像头安装好之后，摄像头在三维场景中的位置就不再变化了，拍摄的画面的背景也就固定不变了。这时再从拍摄的背景画面中找到画面的上下边界所对应的场景实际位置，再到场景中实地中测量出摄像机的安装高度a和画面的上沿和下沿距离摄像头垂平面的距离b和c。

由于画面都是由一个个的像素组成的，所以如果只通过单幅的画面计算目标距离和尺寸，那么计算的精度就不会超过目标在图像中单个像素所代表的尺寸。但在一般的视频监控中这个识别精度也足够用了。

接下来可以通过几何计算得到画面每一个像素所对应的实际场中地面的大小尺寸。

只要知道目标的底部在地面的位置就可以计算出目标到摄像头垂平面的距离。

但是画面中的目标并不是贴合在地面上的，而一般是直立在地面上的，所以不能将目标在地面上的投影所对应的像素所代表长度当作目标的高度。目标的实际高度还需要通过计算目标垂线与摄像机的到目标的连线夹角计算得到。

接下来的计算如图1、图2。

图1

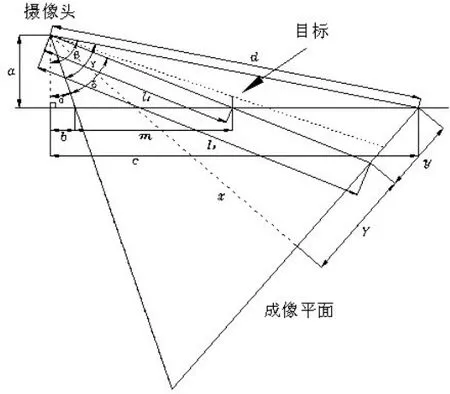
图2

（2）已知a、b、c、N、P为单位像素、N为图像的Y轴上总像素数、y为目标下沿坐标值，求Y轴方向y0到yN每个像素所对应地面的实际长度值lyd。

l1为摄像头到目标所在地面的距离，l2为摄像头经过目标所在地面到成像平面的距离，通过这两个参数的比值就可以得到目标所在的地面点和对应成像平面点尺寸比例关系，只要知道这个成像平面的点所对应的像素代表的尺寸，就可以计算出该地面点的实际尺寸。

用这个方法就可以建立起一个函数：

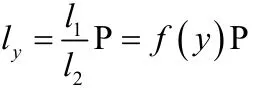
它表达的是在图像中Y轴上的每个像素对应地面的尺寸ly

如图 2所示l1为摄像头到目标所在地面的距离，由勾股定理可知它可以由摄像头到地面的距离a和图像画面的下沿到摄像头垂平面的距离b与图像画面的下沿所显示的地面点到目标所在地面的距离m之和得到，如公式(3)。

同样如图2所示l2为摄像头经过目标所在地面到成像平面的距离，它可以由摄像头到成像平面的垂直距离也就成像平面Y轴的中点距离x与成像平面的Y轴中点到目标在成像平面投影的位置的长度Y，用三角定理计算得到，如公式(4)。

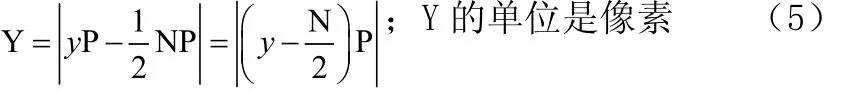
Y可以由目标在图像中的坐标值yP减去成像平面的Y轴长度的一半即得到，如公式(5)，N为图像的Y轴向总像素数，P为单位像素。

将公式(5)代入公式(4)得到公式(6)。

是假设的成像平面的Y轴和Y轴的两个端点与摄像头的连线形成的等腰三角形的垂直高度。

假设投影平面所处的位置是Y轴的上端点也就是0像素位刚好是在图像中显示的地面最远处的点。

由于有上述关于投影平面位置的假设所以d可以由公式(8)得到，a和c是已知的。

将公式(8)代入公式(7)得到公式(9)。

将公式(9)代入公式(6)得到公式(10)。

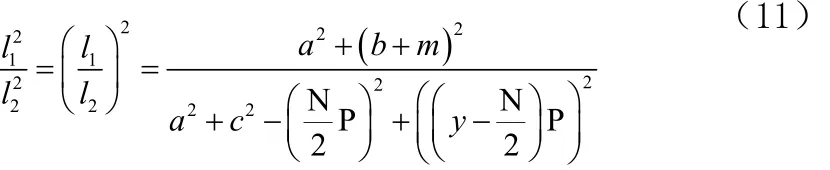
将公式(3)和公式(10)相除得到公式(11)。

公式(11)中y是自变量，是图像中Y轴上的任意一点。现在这个公式中只有m是未知量。下面要得到m和已知量的相关性。m是像画面的下沿所显示的地面点到目标所在地面的距离。

摄像头与地面的垂线和摄像下视野线的夹角为 ，得到公式(12)。

摄像头与地面的垂线和摄像上视野线的夹角为 ，得到公式(13)。

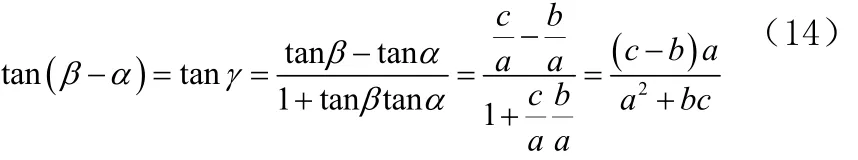
由三角定理得到摄像头的上下拍摄视角β-α也就是的正切值，得公式(14)，可以推导出公式(15)得到 ：

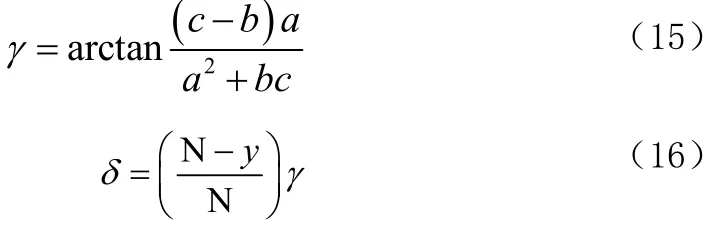
δ为摄像下视野与摄像头到目标地面点的连线之间的夹角，对这个夹角δ的计算进行了简化，使用了公式(16)，这个公式的前提假设就是在摄像机不是在大广角的情况下，图像中的Y轴上的任意一个像素所占的摄像头的视角是一样大的。但实际上并不一样，从几何图形中可以看出如果成像面是球面的，这个公式就是精确的了。但是一般情况下获取目标参数的精度并不需要特别的高，所以为了简化算法提高效率使用公式(16)进行后面的计算。

由余切定理得到公式(17)。

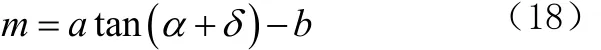
由公式(17)可以推出公式(18)得到m。

那么b+m就是目标到摄像机的垂平面的距离，b+m由前面的公式可以看出目标在不同的Y轴上的像素就有不同的距离值。

公式(19)表达的是在这个假设成像平面中一个像素所对应具体的长度。

将公式(18)和公式(19)带入公式(11)得到公式(20)。

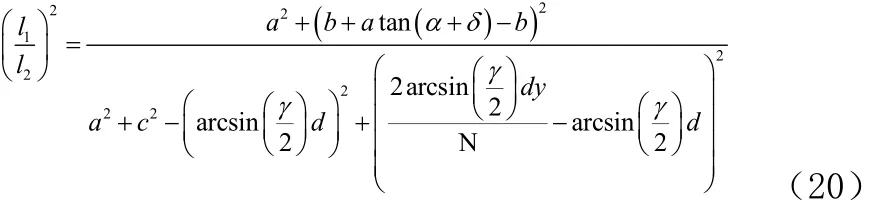
这里我们定义l1与l2之比为f(y)，由公式(20)右边可知这个比例只与变量y相关，得到公式(21)。

下面就是单位换算的问题， f(y)表达的是在图像中Y轴上的任意一个像素(y坐标)和对应的地面尺寸比例值，它没有单位，这时只要把公式(19)带入公式(21)替代l2就可以得到的是ly也就是图像中不同的y坐标对应的实际地面尺寸公式(22)、(23)。

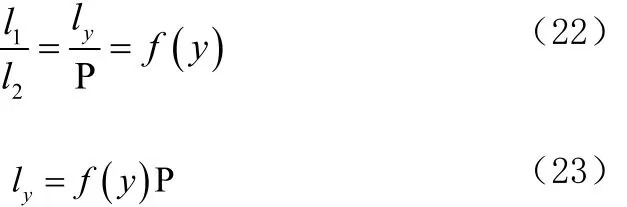
这样得到了一组数据就是：在 Y轴方向y0到yN每个像素所对应的ly长度值。另外根据相似三角形原理，在X轴方向同一水平线上的所有x点的实际对应长度值是与本水平线对应的y点的ly相同。

ly实际上是图像中某个像素对应的地面的长度，还不是像素对应目标的高度值。真正的目标一般是直立在地面上的。获得的目标像素高度和宽度值实际上是目标i在摄像头所处的角度下，目标所遮挡地面的长度宽度在投影图像中反映出的像素数量。

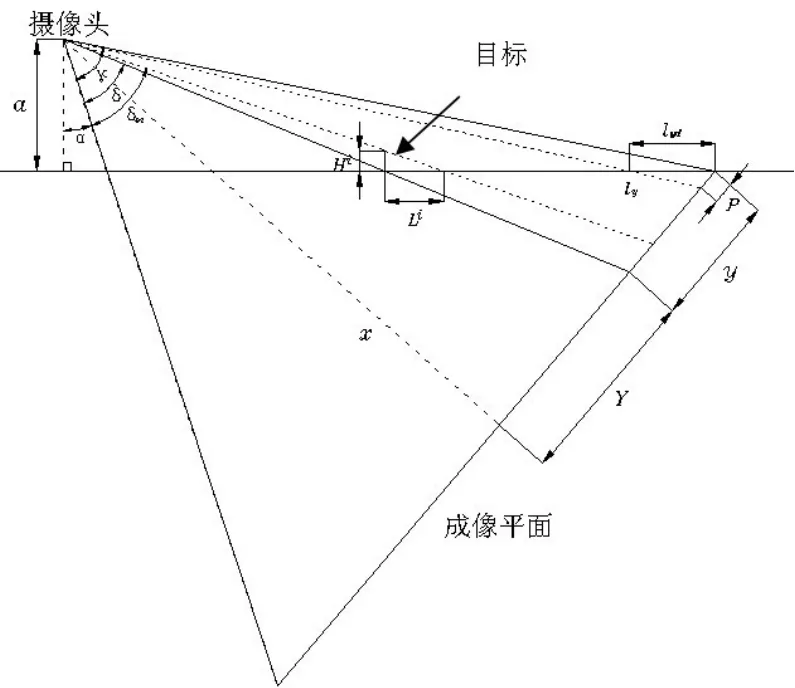
图3

上述方法得到的ly是视频图像中的单个像素对应地面尺寸，因为ly是单个像素的边界所对应的长度，为了更准确的表示像素对应的长度做如下处理

这样就得到一张表。表示Y轴方向y0到yN每个像素所对应地面的更为准确的实际长度值lyd。

（3）求目标i的实际高度和宽度Hi、Wi

计算对象 i的真实高度Hi可以先计算出摄像机到目标顶部 y0i的连线与地面垂线的夹角，通过这个角度和目标在地面上的投影长度换算出来。

假设图像中的目标一般是垂直立在地面上的可以得到公式：

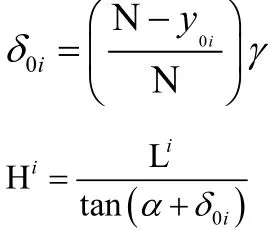
在目标的宽度上也就是X轴上，由于相似三角形的原理目标在地面的投影不随着角度发生变化，所以可以直接由上一步的计算获得不需要进一步处理。

通过上述方法这可以获得一个物体长（高）宽的实际尺寸，但由于上述方法中存在简化和近似算法的原因，还有镜头和目标轮廓的识别受到各种外部环境和算法局限的影响，得到的尺寸还是一个近似值，并不是很精确。上述方法如果使用在变形不是非常严重的情况下还是可以用于分辨目标的。

4 计算产生的误差分析

首先是图像的分辨率对误差的影响，像素的数量越大分辨率越高也就是N越大误差就会越小；另一方面目标与摄像镜头的距离越远，目标在图像中的变形就越小，计算的精度就会越高；另外目标距离过远时，目标所占据的像素就比较少，每个像素所代表长度就比较大，这样会造成目标提取精度对尺寸的影响巨大。

另外最大的计算误差出现在每行像素对应的在摄像头中的视角并不一样，大广角下误差会较大。因此的计算与实际情况就会偏差很大。

为摄像下视野与摄像头到目标地面点的连线之间的夹角，对这个夹角δ的计算进行了简化，得到了公式(16)，这个公式的前提假设就是在摄像机不是在大广角的情况下，图像中的Y轴上的任意一个像素所占的摄像头的视角是一样大的。但实际上并不一样，从几何图形中可以看出如果成像面是球面的，这个公式就是精确的了。而一般情况下获取目标参数的精度并不需要特别的高，所以为了简化算法提高效率应使用公式(16)进行后面的计算。

5 结束语

本算法只适合于在地面上的目标，对于空中的目标就不再适用。

改进算法可以使其适用在场景中的地面在照片中只占用下部的一部分的情况，这样该算法可以更好的用于不同的场景条件

[1] 游素亚.立体视觉研究的现状与进展[J]中国图象图形学报,1997,(01).

[2] 赵勋杰,高稚允.光电被动测距技术[J].光学技术,2003,29(06).

[3] 黄桂平,李广云,等.单目视觉测量技术研究[J].计量学报,2004,25(04).

[4] Xiong,Y.and Shafer,S.Depth from Focusing and Defocusing[J].Proceedings of the DARPA Image Understanding Workshop.1993:967-976.

[5] Nayar,S.K.Shape from Focus System[J].Proceedings of the IEEE Computer Society Conference on Computer vision and Pattern Recognition,Champaign,Illinois,1992:302-308.

[6] M.Subbarao,and J.K.Tyan,The Optimal Focus Measure for Passive Autofocusing and Depth-from-Focus[J].Proceedings of SPIE conference on Video metrics IY,Vol. 2598, Philadelphia,1995,2598:89-99.

[7] Pentland,A.P.A New Sense for Depth of Field[J].IEEE Trans.PAM19.1987:523-531.

[8] A.N.Rajagopalan,S.Chaudhuri.Space-Variant Approaches to Recovery of Depth from Defocused Images[J].Computer Vision and Image Understanding,1997,68(3):309-329.

TP391.41

A

1008-1151(2011)08-0001-05

2011-05-23

陈大海（1975－），男，广西大学计算机与电子工程学院讲师，研究方向为计算机视觉。