基于提升小波变换的容栅传感器输出信号降噪*

梁高翔，马铁华* ，张艳兵

(1.中北大学电子测试技术国家重点实验室，太原 030051;2.中北大学仪器科学与动态测试教育部重点实验室，太原030051;)

容栅传感器具有体积小、功耗低、结构简单、适应性强、抗干扰能力强、温度稳定性和动态响应特性好等优点，已经广泛应用于转轴的转速、位移和扭矩测试［1］。但是在测量的过程中，受到外界因素影响，其输出信号容易混入各种噪声，导致无法对检测数据进行准确的数值分析，为了保证后续处理的正确性，需要对信号进行降噪处理。

传统降噪方法主要有线性滤波和非线性滤波两种，其在信号处理中得到了广泛的应用，但是仍然存在无法刻画信号的非平稳特性，无法得到信号的所有有用信息等问题［2－3］。传统小波降噪方法采用一个小波基函数，能以不同尺度逼近真实信号，但是经阈值处理后某些信息会被当做噪声滤掉，丢失了部分有用信息［4］。

第二代小波在1996年由Sweldens提出后，在信号处理领域得到了广泛应用。它不依赖于Fouerier变换，同样可以获得与经典小波相同的时频特性，计算速度快，计算时无需额外的存储开销［5］。本文采用基于提升小波的降噪方法，对容栅传感器的转速输出信号进行降噪处理，并与传统小波降噪进行对比，从而验证了提升小波变换在工程应用中的合理性和可行性。

1 容栅测速和提升小波变换的基本原理

1.1 容栅测速的基本原理

容栅的结构如图1所示，间隔相等，总长度为旋转轴周长。容栅测速整体结构如图2所示，容栅1和容栅2相互交叉贴在轴承座内侧(静止)，容栅3贴在旋转轴外侧(容栅3分别于容栅1和容栅2构成两组电容)。当转轴以速度V(rot/s)旋转时，两组电容值由小到大再由大到小周而复始地呈三角波变化，电容变化经信号调理电路转换为电压信号，并通过提升小波变换法对其进行降噪处理。以容栅1和容栅3这组电容为例，假设某段时间内正弦波的个数为N，单个容栅宽度为W，每次记录容栅个数的时间为t，容栅所在位置处的半径为R，则转速为:

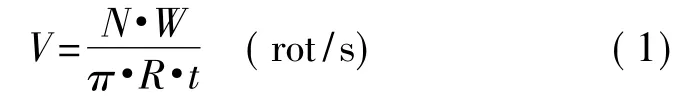
图1 容栅结构示意图

图2 容栅测速的整体结构示意图

测量转轴转速传统方法有光电码盘、光栅盘、旋转变压器、电阻应变片等，这些方法的共同缺点是不适应恶劣的环境，从而降低了其测试精度、缩短了其工作寿命［6－7］;而容栅传感器实现了在旋转轴上无需连线输出、测试电路外置、温度稳定性好、寿命长、可靠性高［8］，在测量转轴转速方面具有其他传感器无可比拟的优势。

1.2 提升小波变换的基本原理

提升小波［9］的分解和重构两个过程，如图3所示。

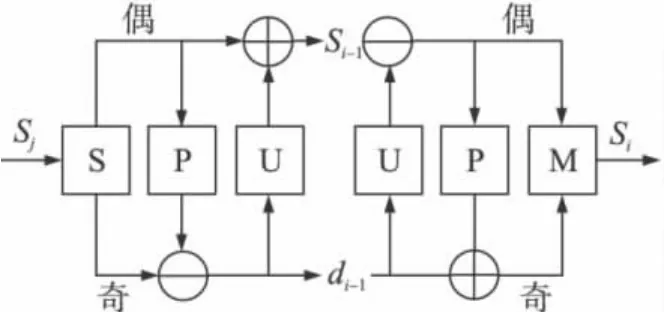
图3 提升方案原理图

1.2.1 分解过程

提升小波的分解过程由分解、预测和更新3部分组成。

(1)分解是由信号的奇偶性将原始信号si分解为两个较小的偶信号序列si－1和奇信号序列di－1，即si－1=s2n，di－1=s2n+1(n=1，2，3…)。

(2)预测是在原始信号相关性的基础上用si－1来预测di－1，用预测误差 δ=di－1－P(si－1)来代替di－1，其中P为预测算子。

(3)更新是通过di－1来更新si－1，亦即用 ξ=si－1+U(di－1)来代替si－1，其中U为更新算子。

1.2.2 重构过程

重构过程是分解过程的逆过程，包括反更新、反预测和合并。

(1) 反更新是在给定si－1和di－1的基础上，由式(2)可恢复偶序列s2n。

(2)反预测是由式(2)所得的s2n和给定的di－1，由式(3)反预测s2n+1。

(3)合并是由s2n和s2n+1融合得到原信号si。

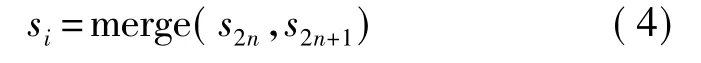
2 仿真信号分析

现以一维信号为例来阐述提升小波降噪的过程。

(1)对某一维信号进行多尺度小波分解;

(2)对分解得到的高频细节信号进行阈值处理;

(3)将逼近信号和经过阈值处理后的细节信号进行小波重构，得到降噪后的有用信号。对提升db5小波用于信号降噪时，小波系数用软阈值法处理［10］:

其中τ为阈值，Med为中值函数。

(4)以均方差(MSE)和信噪比(SNR)作为降噪效果好坏的评价标准，SNR越大，MSE越小，降噪效果越好。

其中xi为信号的准确值，x'i为重构信号，L为信号长度。

表1是分别采用传统小波法和提升小波法对一维Bumps和Doppler两种信号进行降噪处理的效果比较。

表1 两种小波降噪效果比较

由表1可知，对此信号而言，提升小波获得了较大的信噪比和较小的均方差，取得了较好的降噪效果。

3 实测信号分析

用传统小波降噪方法和提升小波降噪方法分别对容栅传感器的转速电压输出信号进行降噪处理，图4为其输出的原始转速信号的电压变化曲线，能粗略分辨出是一正弦波曲线。其中传统小波法对db5小波进行5层小波分解，并采用软阈值降噪［11－12］，其结果如图 5所示;提升小波法对提升的db5小波进行5层小波分解，也采用软阈值降噪，其结果如图6所示。

图4 原始转速信号

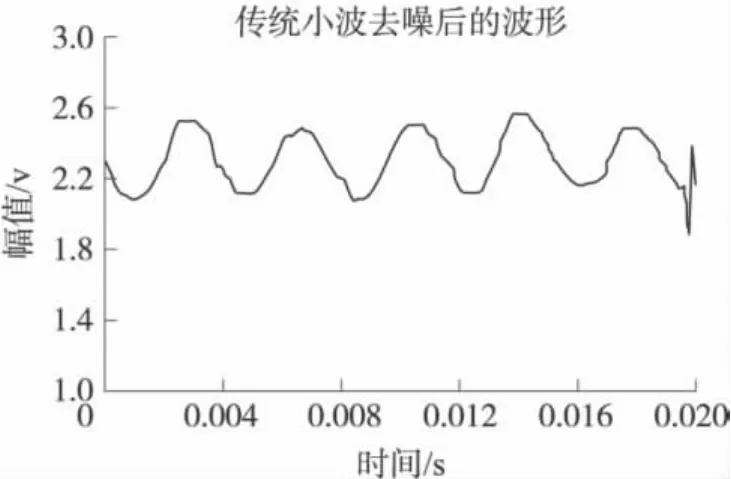
图5 传统小波降噪结果

图6 提升小波降噪结果

由图4可知，由于受到寄生电容和轴旋转时振动造成的影响及外界环境的干扰，致使容栅传感器原始的转速输出信号含有大量的噪声，无法精确地分辨出波形的周期和幅值，给理论分析和数学建模带来了很大的难度和误差。

由图5和图6可知，应用传统小波法对其原始转速电压输出信号进行降噪处理后，其大部分高频信号已被滤掉，但是同时波形也发生了较大程度的失真。分析其原因，可能是容栅传感器转速输出信号较微弱，传统小波法在阈值处理时某些有用信息当成造成滤掉所致。而应用提升小波法能保留其有用信息，且不会造成其波形严重失真，能较准确的测量正弦波的周期与幅值。比较而言，提升小波法在容栅传感器转速输出信号降噪处理方面具有较大的优势。

4 结束语

提升小波变换法具有频域多分辨特性，可实现完全重构，运算速度快，且易在硬件系统上实现。通过对仿真信号和实验数据分析可知，对容栅传感器转速输出信号进行基于提升方案的第二代小波降噪处理，能较好地滤除高频噪声，把有用的微弱信号无失真地跟踪检测出来。精确的有用信号为其后续的理论分析和数学建模提供了有利的保障。其已广泛应用于各种精密仪器输出信号的检测和处理中。但是面对众多的第二代小波提升方案，如何根据不同研究对象的特点选取合适的提升方案是将来研究的重点和难点。

［1］陈伟平，马铁华，裴东兴.嵌入式容栅扭矩转速传感技术［J］.微计算机信息，2009，25(1):153－154.

［2］Manjunath A，Ravikumar H M.Comparison of Discrete Wavelet Transform(DWT)，Lifting Wavelet Transform(LWT)，Stational Wavelet Transform(SWT)and S-Transform in Power Quality Analysis［J］.European Journal of ScientificResearch，2010，39(4):569－576.

［3］周伟.小波分析高级技术［M］.西安:西安电子科技大学出版社，2006:87－129.

［4］刘春树，潘紫微.宋淼第二代小波在振动信号去噪中新方法的研究［J］.机械传动，2008，32(3):64－66.

［5］杨建国.小波分析及其工程应用［M］.北京:机械工业出版社，2005.6.

［6］李军.电阻应变称重传感器蠕变的模型和补偿［J］.传感技术学报，1995，8(3):59－63.

［7］张伟刚，王述祖，梁龙彬，等.光纤光栅与电阻应变片应变测量的对比分析［J］.传感技术学报，2001，14(3):200－205.

［8］傅宗纯，周文祥.基于DSP的容栅传感器输出信号处理［J］.工具技术，2010(1):102－104.

［9］Daubechies I，Sweldens W.Factoring Wavelet Transform into Lifting Steps［J］.Journal of J Math Anal Appl，1998，4(3):247－269.

［10］程正兴，杨守志，冯晓霞.小波分析的理论、算法、进展和应用［M］.北京:国防工业出版社.2007.7.

［11］飞思科技产品研发中心.小波分析理论与MATLAB7实现［M］.北京:电子工业出版社，2005.3.

［12］王昱，张青斌，吴海燕，等.第二代小波在试验数据处理中的应用［J］.弹箭与制导学报，2008，28(6):169－171.