基于ANSYS的机床电主轴温度场计算仿真分析*

李程启 张小栋 张 倩 李 浩

(①西安交通大学苏州研究院，江苏苏州215021;②西安交通大学机械工程学院，陕西西安710049)

制造技术的发展对数控机床的精度和可靠性提出了越来越高的要求，机床的精密化、高速化已经成为一个不可阻挡的发展趋势。在精密加工中，由机床热变形所引起的制造误差占总误差的40% ～70%［1］。在高档数控机床中，影响机床热变形的主要因素有电主轴的热变形、刀具的热变形、进给系统的热变形和床身的热变形等。电主轴作为高档数控机床最重要的零部件之一，其热变形为机床热变形的最重要影响因素［2］，它的性能的好坏直接影响着机床的加工精度和加工产品的质量。电主轴的热变形主要是由电主轴的温度场分布不均匀造成的，因此对电主轴的温度场做仿真分析、减小电主轴的温度场分布不均匀对减小电主轴热变形至关重要。

对主轴系统热特性的研究，近年来主要集中在主轴—轴承的热特性研究上［2］。韩国的Kim等人对轴承发热对主轴刚度的影响做了大量研究［3］，广东工业大学的张伯霖教授对主轴系统的温度场做了仿真分析，并且分析了主轴转速对轴承温升的影响［4］，中国工程物理研究院的胡秋等人对电主轴单元的热-结构特性做了动态分析，并且提出了改善电主轴热态特性的措施［5］。这些研究虽然对改善电主轴系统的热态特性有很大的帮助，但是他们都是总体研究主轴系统的温度场，没有单独拿出主轴这一子单元进行分析，而且只是被动地改善电主轴温度场或者增加辅助结构进而减小热变形。

本文基于此，单独对主轴进行热分析，得出主轴的温度场分布，直接为改善主轴的热态特性提供依据，并且提出主动改善热变形引起的加工误差的方案。

1 电主轴的特点及热态特性

高速电主轴是数控机床的核心功能部件，它具有结构紧凑、惯性小、转速高、动态特性好等诸多优点［6］，在高速机床中得到广泛的应用。其典型结构如图1所示。

主轴电动机定子直接安装在主轴箱的壳体中，机床主轴与电动机转子连成一体。电动机转子回转则带动机床主轴旋转，省去了机械传动环节，实现了机床的“零传动”，但是这也对主轴电动机的散热极其不利。

电主轴的热源分为内部热源和外部热源。内部热源主要有电动机定转子的损耗发热和支撑轴承的摩擦发热两大类。外部热源主要是指环境温度变化及其他各种能散发出热量的物质。电主轴的传热主要表现为:

(1)电动机与油水热交换系统的对流换热;

(2)轴承与润滑系统的对流换热;

(3)电动机定子与转子之间的气隙传热;

(4)电主轴前后密封环的对流换热;

(5)电主轴与外部空气的传热［7］。

2 热边界参数的分析计算

2.1 热源计算

在电主轴系统中，内部热源主要有主轴电动机损耗发热与支撑轴承的摩擦发热。在利用ANSYS仿真分析时，主轴电动机转子以生热率的形式加载，轴承的热量以热流密度的形式加载。

2.1.1 主轴电动机生热率的计算

电动机的额定功率损耗全部转化为热量，且其中2/3热量由定子产生，1/3热量由转子产生［8］。在本文中选择西门子IPH2113-6WF4型号的主轴电动机，其参数如表1所示。

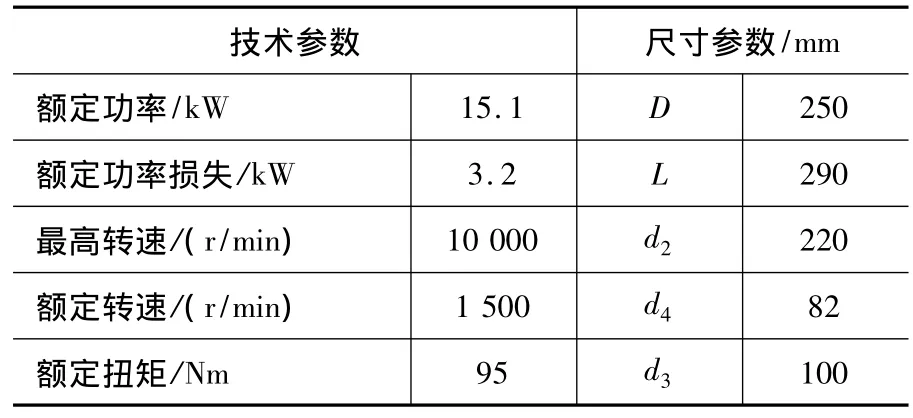
表1 主轴电动机参数

电动机总发热功率即为额定功率损失，且电动机转子的发热量占总发热量的1/3，电主轴转子的生热率q为

式中:Q为发热功率，W;V为体积，m3。

2.1.2 支撑轴承热流密度的计算

轴承产生的热量主要来自于轴承的转动摩擦。在本文中，前轴承选择SKF的71915CE/HC角接触球轴承，后轴承选择SKF的61913深沟球轴承。本次计算中，假设加工工件为45钢，电主轴的转速为 8 000 r/min。前后轴承的参数如表2所示。

表2 前后轴承参数

轴承的发热功率Q轴承为

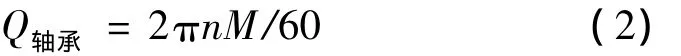
式中:M为轴承摩擦总力矩，N·mm;n为轴承内圈转速，r/min。

轴承摩擦总力矩M由轴承空转时润滑剂粘性产生的摩擦力矩M0和与速度无关的载荷作用下产生的摩擦力矩M1两部分组成，即:

(1)M0的计算

当运动粘度ν与转速n的乘积大于0.002(m2/s)·(r/min)时

当运动粘度ν与转速n的乘积小于0.002(m2/s)·(r/min)时

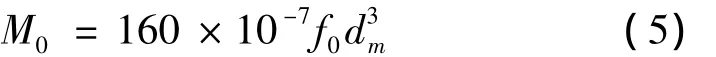
式中:dm为轴承的平均直径，mm;f0为取决于轴承设计和润滑方式的系数，对于角接触球轴承油气润滑方式，f0=1;ν为在工作温度下润滑剂的运动粘度(对于润滑脂取基油的粘度)，m2/s。

(2)M1的计算

摩擦力矩M1反映了弹性滞后和局部差动滑动的摩擦功耗，可按下式进行计算:

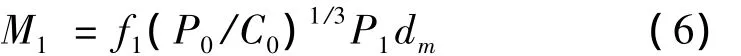
式中:f1为与轴承类型和所受负荷有关的系数，角接触球轴承f1=0.001;dm为轴承的平均直径，mm;P0为轴承的当量静载荷，N;P1为决定摩擦力矩的当量载荷［9］，N。

2.2 对流换热系数的计算

对流换热系数是指流体与固体表面之间的换热能力，即物体表面与附近空气温差1℃、单位时间单位面积上通过对流与附近空气交换的热量。在本次分析中，主要有定转子之间的气隙传热、转子端部传热、主轴头部运动外表面与周围空气的对流换热、电主轴内部的对流换热和电主轴内孔与空气间的对流换热。分别计算如下:

2.2.1 转子与气隙间的对流换热系数

定、转子气隙中的气体在纯层流状态下，热量是通过纯导热由一个表面传到另一个表面，并且热交换不取决于转速。

(1)Re被用作层流和紊流的判据，定义为

式中:u为流体的特征速度，m/s;ν为流体的运动粘度，m2/s;D为几何特征的定型尺度，m。

(2)当定、转子气隙有层流底层的紊流状态时，按下式计算努谢尔特数Nu为

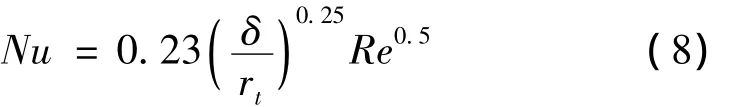
式中:rt为密封环气隙的平均半径，m;δ为定、转子间的气隙，m。

(3)由努谢尔特数Nu即可求出管内流体强迫对流换热系数α为

式中:λ为流体导热系数，W/(m·K)。

2.2.2 转子端部与外部空气的对流换热系数

转子端部的传热问题主要是与周围空气的对流换热和辐射换热。该热交换的换热系数αt为

式中:u为转子端部转速，r/min。

2.2.3 主轴头部运动外表面与周围空气的对流换热系数

此系数可用以下的多项式函数来拟合［10］:

式中:c0、c1、c2为实验测得的常数，分别取为 9.7、5.33、0.8;u为头部转速。

2．2．4 电主轴内部的对流换热系数

此部分换热系数的计算和转子端部与外部空气的换热系数计算方法相同。

2．2．5 电主轴内孔与空气间的对流换热系数

此部分换热系数的计算和转子与气隙间的对流换热系数计算方法相同。

通过以上计算，各部分的热边界参数如表3所示。

表3 热边界参数

3 电主轴温度场热分析

3.1 稳态热分析

电主轴整体上可认为是轴对称结构，在建模时可以只建模型的剖面的一半。在网格划分时，采用PLANE55单元划分网格，并且控制网格的大小。PLANE55单元可用于平面或轴对称结构，具有热传导特性，该单元有4个节点，节点自由度为温度。

对主轴电动机转子的热量采用生热率的方式加载，对轴承的热量采用热流密度的方式加载。通过ANSYS仿真，得到图2所示的稳态温度场分布结果，其中最高温度为171.7℃，在电主轴的中间位置，即电动机转子的安装位置处。最低温度为91.8℃，分布在电主轴的右端(电主轴前端)，主要是由于电主轴的右端离热源相对较远。从图2中还可以看出，在电主轴的两端安装轴承的位置处温度也较高，达到120℃，这是由于轴承摩擦发热造成的。

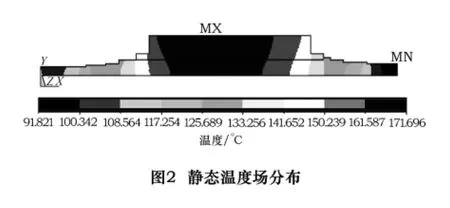
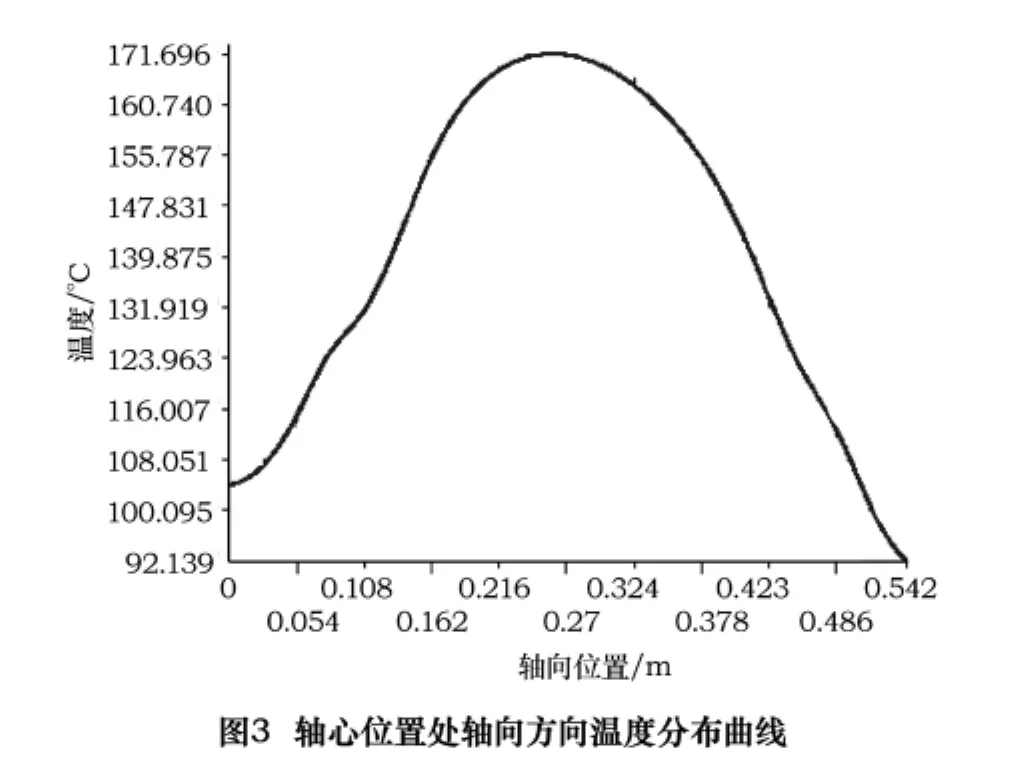
取电主轴轴心位置处以轴向方向为路径，得出温度分布曲线如图3所示，整体来看，中间温度高，两端温度逐渐降低，整个电主轴的温度场分布及其不均匀，这也是造成电主轴热变形的主要因素。

3.2 瞬态热分析

电主轴进行瞬态热分析，设置时间为5 000 s。得到瞬态分析的温度场分布如图4所示。在5 000 s时，电主轴的温度场基本达到平衡。

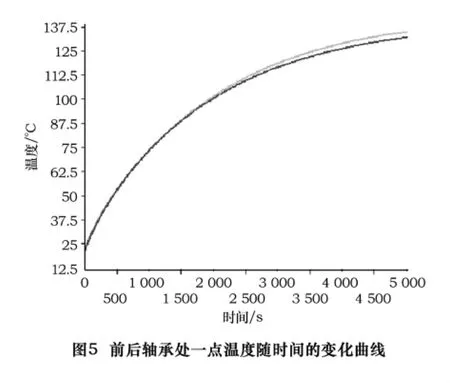
分别取电主轴上前后轴承处的一点得出其温度随时间的变化曲线如图5所示。

由图中温度变化曲线可以看出，前后轴承处的温度变化基本一致，此为一种较好的结果，前后轴承温度对称。同样，由此引起的热变形也是一致的，避免了由于前后轴承热变形的不同造成主轴翘曲的情况。说明了所选的支撑方式与润滑方式是较为理想的。

4 改善温度场分布及减小热变形的措施

电主轴的温度场分布不均匀是由于电主轴冷源和热源综合作用的结果，而电主轴的热变形主要是由于电主轴温度场的分布不均匀造成的。综合以上仿真分析，提出以下措施:

(1)改善主轴电动机的油水冷却系统的参数，如循环冷却水的流速;

(2)改善轴承的油气冷却润滑系统的参数，如压缩空气的压力、压缩空气的流速;

(3)选择合适的轴承支撑系统，使电主轴两端的轴承的温度场分布基本一致，从而使其热变形基本一致，避免电主轴发生翘曲;

(4)通过对电主轴工作在不同工况下的模拟仿真，得出电主轴的热变形曲线，建立数学模型，将其嵌入到数控系统之中，使其在不同工况下建立不同的软件补偿方案，减小电主轴热变形对加工误差的影响。

5 结语

通过以上分析可以知道在电主轴的温度场分布中，在主轴的中间温度较高，从中间向两端温度逐渐降低，并且在轴承处温度相对较高。在改善电主轴温度场分布上，可以通过加强主轴电动机和轴承的冷却等方式加强散热。在减小电主轴由于温度场分布不均匀造成的热变形上，可以通过合适的散热方式使轴承处温度变化基本相等使主轴不至于发生翘曲，还可以通过软件补偿这一主动改善热变形引起的加工误差的方法来减小热变形。

［1］RAMESH R.E1T or Compensation in machine tools—a review part l/:thermal errors［J］.International Journal of Machine Tools ＆ manufacture，2000，40:1257-1284.

［2］郭策，孙庆鸿.高速高精密数控车床主轴系统的热特性分析及热变形计算［J］.东南大学学报，2005，35(2).

［3］KIM S M，LEE S K.Prediction of thermo-elastic behavior in a spindle-bearing system considering bearing surroundings［J］.International Journal of Machine Tools＆ Manufacture，2001，41(6).

［4］郭军，张伯霖，肖曙红，等.基于热接触分析的电主轴热态特性研究［J］.机床与液压，2006(7).

［5］胡秋，何东林.数控机床电主轴单元热——结构特性动态分析［J］.组合机床与自动化加工技术，2006(12).

［6］马丙辉，卢泽生.基于电主轴的高速轴承及其热分析［J］.机械设计与制造，2008(11):11.

［7］张明华，袁松梅，刘强.基于有限元分析方法的高速电主轴热态特性研究［J］.高速加工技术，2008(4).

［8］伍良生，罗吉成，周大帅，等.高速高精密机床主轴温度场的有限元分析［J］.现代制造工程，2008(9).

［9］于翔.主轴系统热变形分析［J］.应用能源技术，2008(10).

［10］黄晓明，张伯霖，肖曙红.高速电主轴热态特性的有限元分析［J］.航空制造技术，2003(10).