基于MATLAB的电能质量周期性扰动分析

赵翠旗，孔会兰

（晋城供电分公司，山西 晋城 048000）

现代社会中，电能是一种最为广泛使用的能源，其应用程度是一个国家发展水平的主要标志之一。随着科学技术的发展、微电子器件与电力电子技术的广泛应用，人们对电能质量的要求越来越高；同时由于扰动性负荷（如非线性、冲击性或不对称负荷）接入电力系统及其他扰动源（系统短路故障）的存在，造成了大量的电能质量问题，谐波污染、三相不平衡度、跌落和闪变也越来越严重。电能质量问题不仅对电网的安全运行不利，严重干扰电网的稳定经济运行，还能造成某些对电能质量要求较高的电力用户（如纺织行业、机械电子制造业等）严重的经济损失。

电能质量问题的产生可能来源于供电方的输配电系统、用户端的不合理用电及雷电等自然现象。只有对电能质量进行有效地监测，才会对问题的产生和影响有清楚的认识，为电能质量的改善、供用电双方的协调和供用电市场的规范提供真实依据，以便采取有效的解决措施。为保护电力系统安全和用户的用电安全，迫切需要对电能质量进行监测和分析，以提供整改方案、加强防范措施、限制强干扰源（如谐波源），从而保护电力系统的安全、可靠、经济运行，并保护电力用户的合法权益。

法国学者M. Grimaud在地形学的基础上提出了一种极值点评价测度——Dyn测度（Dynamics），以解决噪声环境下的极值点提取问题。Dyn 测度能够反映信号极值点的结构特征，并可识别信号的畸变极值点。这一特点使其非常适合电能质量扰动检测。本文在此基础上，利用MATLAB编写程序，对电能质量一般性周期性扰动进行分析，对扰动信号进行实时定位，谐波扰动也可以看做是周期性扰动的特例，对于谐波扰动，更关心的是它的测量指标、谐波畸变率和各次谐波含有率，所以此处不再选择谐波扰动信号进行分析。

本文采用的是MATLAB软件，其名称源自Matrix Laboratory，它是由美国MathWorks公司推出的一种科学计算软件，专门以矩阵的形式处理数据。MATLAB将高性能的数值计算和可视化集成在一起，并提供了大量的内置函数，从而使其广泛地应用于科学计算控制系统、信息处理等领域的分析、仿真和设计工作中。而且利用MATLAB产品的开放式结构，用户可以容易地对MATLAB的功能进行扩充，从而在不断深化对问题认识的同时，逐步完善MATLAB产品，以提高产品自身的竞争力。

1 MATLAB编程的优点

用MATLAB来解算问题要比用C、FORTRAN等语言简捷得多。MATLAB是国际公认的优秀数学应用软件之一，其优点如下：

（1）以矩阵和数组为基础的运算，不需要预先定义变量和矩阵（包括数组）的维数，可以方便地进行矩阵的算数运算、关系运算和逻辑运算等。而且MATLAB有特殊矩阵专门的库函数，可以高效地求解诸如信号处理、图像处理、控制等问题。

（2）语言简洁，使用方便。MATLAB程序书写形式自由，函数名和表达式更加接近书写计算公式的表达式。

（3）强大的科学计算机数据处理能力。比起 C语言，在计算要求相同的情况下，使用MATLAB编程，工作量会大大减少。MATLAB的这些函数集包括从最简单最基本的函数到诸如矩阵、特征向量、快速傅里叶变换。

（4）强大的图形处理功能。MATLAB具有强大的以图形化显示矩阵和数组的能力，同时它能给这些图形增加注释，对图形进行标注和打印。

（5）应用广泛的模块集合—工具箱。MATLAB的一个重要特色就是具有一套程序扩展系统和一组称之为工具箱的特殊应用子程序，每一个工具箱都是为某一类学科专业和应用而定制的。目前，MATLAB已经把工具箱延伸到了科学研究和工程应用的诸多领域，如数据采集、数据库接口、概率统计、样条拟合、优化算法、神经网络、小波分析、电力系统仿真等都在工具箱家族有了一席之地。

（6）可扩充性强，具有方便实用的应用程序接口和发布平台。MATLAB不仅有着丰富的库函数，在进行复杂的数学运算时可以直接调用。而且用户还可以根据需要，方便地在MATLAB环境中调用其他用C语言编写的代码，也可以在C语言程序中调用 MATLAB计算引擎来执行 MATLAB代码。新版本的MATLAB可以利用MATLAB编译器和C/C＋＋数据库和图形库，将自己的MATLAB程序自动转换为独立于MATLAB运行的 C/C＋＋代码。允许用户编写可以和 MATLAB进行交互的C/C＋＋语言代码。另外，MATLAB网页服务程序还容许在Web应用中使用自己的数学和图形程序。

（7）源程序的开放性。除内部函数外，所有MATLAB的核心文件和工具箱文件都是可读可改的源文件，用户可通过对源文件的修改以及加入自己的文件构成新的工具箱。

MATLAB产品族可以用来进行以下工作：①数值分析；②数值和符号计算；③工程与科学绘图；④控制系统的设计与仿真；⑤数字图像处理；⑥数字信号处理；⑦通讯系统设计与仿真；⑧财务与金融工程。

编写MATLAB程序是在*.m格式文件中进行的，其基本操作是：执行“File”菜单下的“New”命令，在弹出的对话框中，选择“M－File”子选项，生成工作环境，进行程序编写，程序编写完成，运行时点击工具栏中的“Save and run”命令。

2 简述MATLAB函数与指令

在进行程序编写时，会用到不同的MATLAB函数与指令来实现程序的功能，这里仅对几个比较重要的函数和指令进行描述。

2.1 数据载入指令

将 txt文档中的数据载入 MATLAB中可以用的命令有很多，本文程序中用到的是load命令和importdata命令。

2.2 画图指令

在MATLAB中进行数据可视化，使用最频繁的绘制函数就是plot函数，该函数能够将向量或者矩阵中的数据绘制在图形窗体中，并且可以指定不同的线型和色彩。同一个plot函数不仅能绘制一条曲线，还可以一次绘制多条曲线。

plot函数的基本使用格式为：

绘制一条曲线：plot(xdata,ydata,'color_linestyle_marker')；绘制多条曲线：plot(xdata1,ydata2,'clm1',xdata2,ydata2,'clm2',......)；若在绘制曲线时没有指定曲线的色彩、线型和标识符，则MATLAB使用默认的设置。

2.3 选择结构

当判断某一条件是否满足，根据判断的结果来选择不同的解决问题的方法时，就需要使用选择结构。和C语言类似，MATLAB的条件判断可以使用if语句或者switch语句。本文采用的是if语句。

2.4 for循环结构

在解决很多问题时需要使用循环结构，MATLAB中包含两种循环结构：一种是循环次数不确定的 while循环；另一种是循环次数确定的for循环。本文中主要用到的是for循环结构，使用for语句构成循环结构是最灵活、简便的方法，在MATLAB中，for循环的基本结构如下：

for index=start:increment:end

MATLAB语句end

其中，index的取值取决于start和end的值。MATLAB的循环结构也可以进行嵌套使用，使用嵌套的循环需要注意 for关键字和end关键字之间的配对使用。

3 Dyn测度

在了解Dyn测度定义之前，首先要了解两点之间路径的概念。设f（t）为定义在有限区间I上的信号，且满足条件f（t）≥0，可以将各采样点的数值看作是各点的高度。两点之间的路径：设m，n为f上不同的两点，则f上这两点之间的部分称为路径P（m，n），其中，P1为m，PN为n。

（1）路径的Dyn测度：路径P（m，n）的Dyn测度定义为路径上最高点和最低点的高度差。

（2）极小点的Dyn测度：设M为f的一个极小点，如果存在比其更低的极小点，则极小点M的Dyn测度等于由点M通向同高度点的所有路径中最小的路径Dyn测度。极小点M两侧各有一个或多个比点M更低的极小点时，点M两侧也一定存在两个与点M等高度的点N1和N2。由极小点M通向点N1的路径记为P1，由极小点M通向点N2的路径记为P2。极小点M的Dyn测度等于路径P1的Dyn测度和路径P2的Dyn测度中较小者。路径P1的Dyn测度小于路径P2的Dyn测度，所以极小点M的Dyn测度应该等于路径P1的Dyn测度。即：

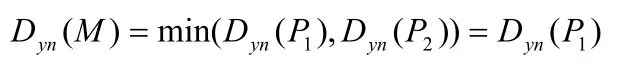
值得注意的是，极小点M的Dyn测度与路径或路径P2的长度无关。极小点M的一侧存在比点M更低的极小点时，意味着只存在路径P1或路径P2，则极小点M的Dyn测度等于路径P1或路径P2的Dyn测度。极小点M为信号的最小点时，设置其Dyn测度等于信号最高点和最低点的高度差。这样，最低点的 Dyn测度比其它极小点的 Dyn测度都大。极大点的 Dyn测度同极小点Dyn测度的定义相仿。

Dyn测度算法能够快速检测信号的所有极值点，并计算各极值点的Dyn测度，其基于溢流仿真的过程描述如下：

设信号f（t）在定义区间I＝[a，b]上含有多个极小值和极大值，hmin和 hmax分别为信号的最小值和最大值。某时刻的溢流水平为 h，对应的溢流区域 C（h）定义为满足 f（t）≤h的所有点t的集合，即：

随着溢流水平的递增，溢流区域不断扩大，直到溢流水平达到h＝hmax时，溢流过程结束，此时的溢流区域为信号的定义区间，即：

溢流过程是一个迭代过程。迭代步长为dh，假设第k步的溢流水平为hk，对应的溢流区域为C（hk）；第k＋l步的溢流水平为 hk＋1＝hk＋dh，对应的溢流区域为 C（hk＋1），则：

如果D为C（hk＋1）的一个连通子集，D与C（hk）可能有下面3种关系：

（1）D∩C（hk）为空集：这种情况下，D是f（t）的一个新的极小点，该新的极小点记为Mj，其高度为hk＋1。

（2）D∩C（hk）不为空集，并且为一个以上的连通成分：这是没有出现新的极小点，也没有出现新的极大点。

（3）D∩C（hk）不为空集，并且为一个以上的连通成分：这种情况下，出现了新的极大点，且该极大点的高度为 hk＋1。该极大点两侧的两个极小点中，较高极小点Mj的Dyn测度为：

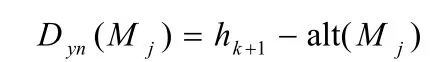
其中，alt（Mj）表示Mj点的高度。

迭代过程结束时，除最低极小点M外，其他极小点的Dyn测度全部得到。而最低极小点M的测度为：

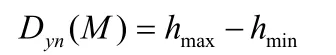
如图1所示，信号发生了周期性畸变，信号的Dyn测度检测结果如图1（b）所示，不同位置出现了幅值不等的Dyn测度，但其分布有一定的规律性：一部分Dyn测度的幅值较大，保持在2.5左右，且均匀分布在每个周期；另一部分Dyn测度的幅值较小，也均匀分布在每个周期。比较两图可知，前者幅值较大的Dyn测度对应信号的峰（或谷）点；而幅值较小的Dyn测度对应信号的畸变点。

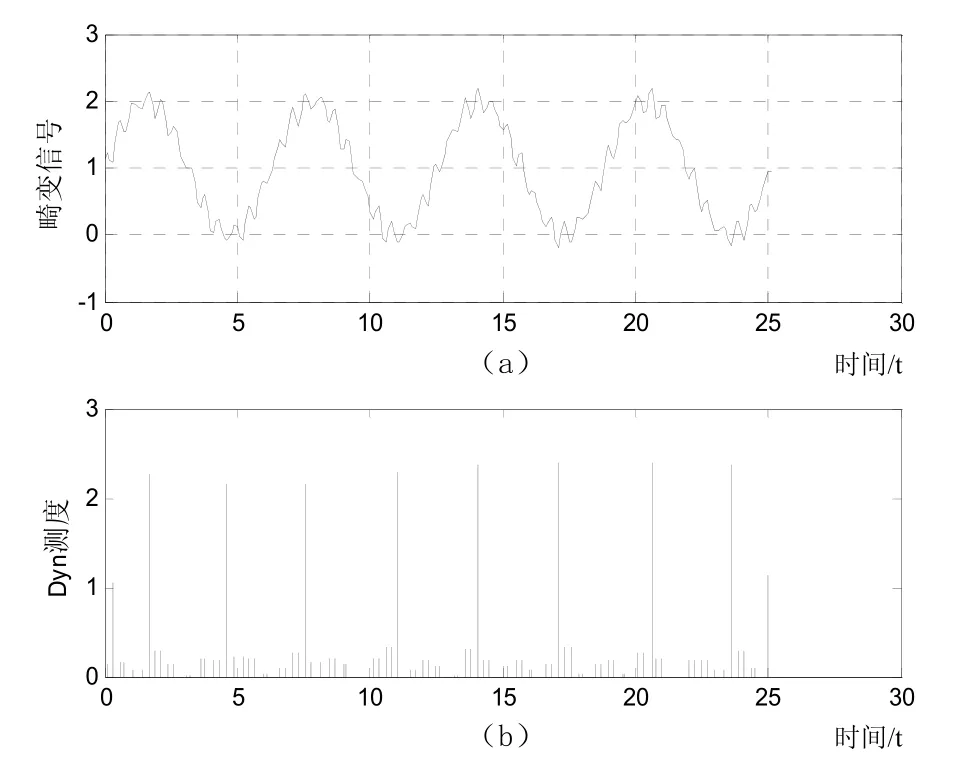
图1 周期性扰动信号检测结果

图2 调节阈值后的周期性扰动的检测结果

取阈值为信号峰/谷点的Dyn测度的15%，得到如图2所示的检测结果。比较图1和图2可知，通过选择合适的阈度，可以消除峰谷点，保留畸变点，达到实时检测周期性扰动信号畸变点的目的。

通过测试可以知道，基于Dyn测度的检测方法能有效地检测多种电能质量扰动（暂态扰动、电压暂降和周期性扰动）；而且算法简单、计算量小，其应用和推广对电能质量监测有重要意义。

1 李瑞峰.10 kV电网电能质量在线监测系统的研究与应用[D].华南理工大学，2006

2 袁之泉.电能质量分析系统研究[D].东北大学，2005

3 宋晓芳.电能质量分析技术研究与实现[D].南京理工大学，2005

4 刘应梅.电能质量扰动检测和分析的研究[D].中国电力科学研究院，2003

5 曹晖.基于DSP的电能质量分析系统的开发[D].华中科技大学，2004

6 许康平.电能质量监测装置的研究[D].东南大学，2007