HD油田水平井测井储层参数解释研究

杨 斌，鲁洪江，昌伦杰，梁 珀

(1．油气藏地质及开发工程国家重点实验室 成都理工大学，四川成都610059;2．中国石油塔里木油田分公司 勘探开发研究院，新疆库尔勒841000)

HD油田水平井测井储层参数解释研究

杨 斌1，鲁洪江1，昌伦杰2，梁 珀1

(1．油气藏地质及开发工程国家重点实验室 成都理工大学，四川成都610059;2．中国石油塔里木油田分公司 勘探开发研究院，新疆库尔勒841000)

水平井测井解释，主要体现在测井仪器响应的理论模拟以及各向异性的实验研究方面，远未达到实际水平井测井储层参数解释应用的深度和要求。在对比分析HD油田水平井段与对应直井层段测井响应特征基础上，这里针对水平井段测井曲线进行了校正，提出使用直井取芯物性数据刻度水平井段测井曲线，来建立适应于水平井段井眼和曲线特征的孔隙度、渗透率神经网络解释模型，进而对整个研究区水平井段进行测井储层参数解释和评价。通过用直井岩芯物性对测井解释结果的检验表明，水平井测井储层参数解释精度得到了明显改善和提高，能够较好地满足三维地质建模的井属性参数精度要求。

塔里木盆地;水平井;储层参数;神经网络;测井解释

0 前言

水平井是开发油气田，提高采收率的一项重要技术。在新油田高效开发，老油田剩余油挖潜调整，气藏及凝析气藏开发以及注水等领域，都取得了良好的应用效果。水平井关键技术之一的测井解释，能够为油田高效开发解决正确指导钻井中靶及钻井方向，优化完井方案，提高注采效果和实施改良措施提供依据。还可为研究剩余油的分布，开发调整井的设计提供基础数据等［1]。

近年来水平井测井解释研究，主要体现在感应、侧向等测井仪器响应的理论模拟［2～4]，各向异性实验研究［5、6]和井眼轨迹显示软件开发［7～9]等三个方面。目前存在的问题和困难有［10、11]:

(1)计算机模拟研究步履艰难，在该领域已经进入了“瓶颈”地带。

(2)校正图版实用性差。

(3)研究工作大多仍然侧重于理论上的定性描述，与实际应用相距甚远。

HD油田位于塔里木盆地满加尔凹陷北部哈得逊构造带上，北侧与塔北隆起轮南低凸起相接，含油层系为石炭系巴楚组的东河砂岩段CIII［12]。在CIII岩性段已钻有八十余口开发水平井，各井水平井段均测有自然电位、自然伽玛和声波～感应电阻率系列曲线，仅绘制了水平井井眼轨迹图，定性划分了油水层，但均未能使用水平井测井曲线进行定量计算东河砂岩水平井段的孔隙度及渗透率等储层参数［8]。为了充分利用本区大量水平井测井资料，为东河砂岩三维地质建模提供各水平井段平面控制范围内的储层属性参数，以及各井局部平面范围内的储层厚度、含油气性等变化规律，作者从水平井与导眼井对比解释的思路出发，在水平井与直井层段测井响应特征对比分析的基础上，对水平井测井曲线进行了校正。基于直井岩芯物性刻度水平井测井响应，作者建立了神经网络储层参数计算模型［13]，并解释评价了研究区各水平井CIII段的储层物性参数，获得了较高的解释精度，为本区三维地质建模提供良好的数据基础。

1 水平井测井校正

1．1 水平井测井响应特征

由于水平井的井眼轨迹基本沿地层延伸方向，而直井是垂直于地层方向，因此首先要根据水平井测井曲线特征寻找，再与其相对应的直井井段。在对水平井进行深度校直后与对应直井井段测井曲线重叠显示(见图1)，即可直观分析在同一地层的层段内，二者声波时差、电阻率和自然伽玛曲线的异同。

从图1中可以明显看出，水平井声波时差值高于直井对应井段内的声波时差值，地层电阻率与冲洗带电阻率稍高于与其对应的直井段的地层电阻率与冲洗带电阻率。

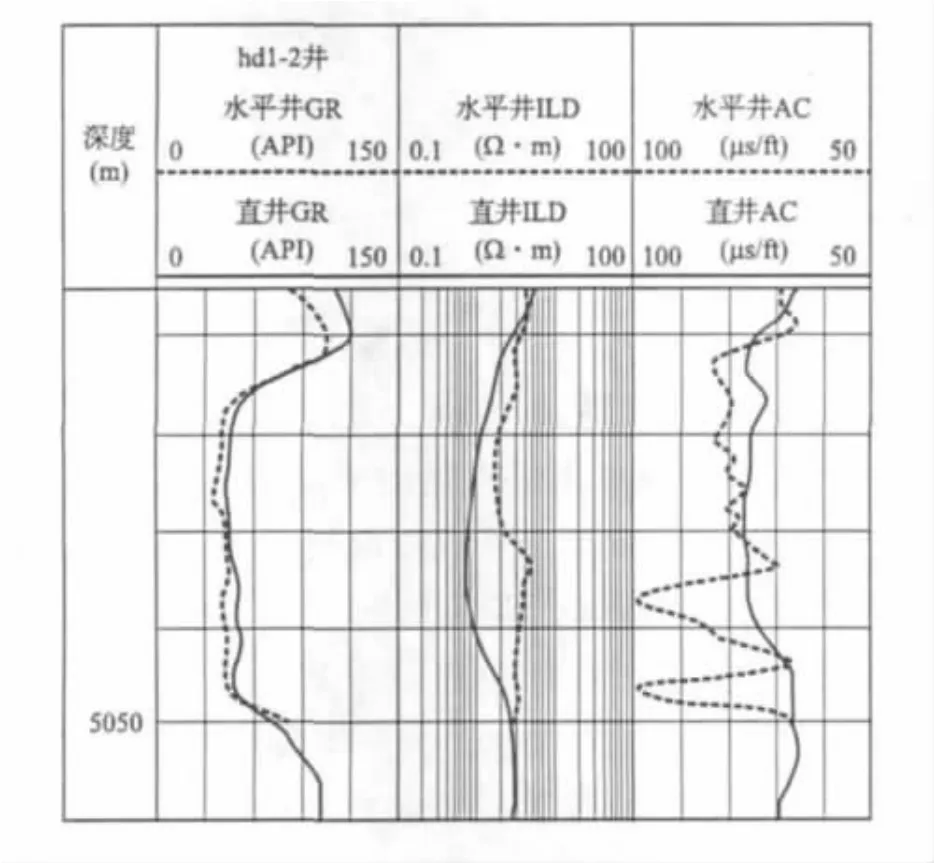
图1 水平井与直井测井曲线重叠对比图Fig．1 Well-logging overlapping comparison of horizontal well versus verticalwell

自然伽玛测量仪器是径向平均测井仪器，当岩性界面不在仪器探测范围内时，自然伽玛曲线测量值不受岩性界面以及邻层的影响，能够反映岩性较真实的自然伽玛特征。导眼井的自然伽玛曲线，与对应层段的水平井校直后的自然伽玛曲线趋势基本相同(见图1)。

1．2 水平井测井曲线校正

作者绘制了二十多口水平井及其对应导眼井内相同层段上的声波时差、电阻率、自然伽玛曲线的频率直方图，从单井各测井曲线的峰值可以看到:在同井同层段上，水平井内的声波时差曲线和电阻率曲线的峰值，普遍高于导眼井中对应层段的测井曲线值。基于对此差异的认识，通过统计对比方法，作者分别对水平井内的声波时差、电阻率和自然伽玛曲线进行校正，以便于使用基于直井测井评价模型来计算水平井的储层参数。

通过对水平井与导眼井中所对应井段的单井声波时差频率直方图峰值比较发现，其中有十二口水平井声波时差曲线高于导眼井的声波时差曲线。导眼井声波时差单井峰值平均值为70.125μs/ft，水平井声波时差单井峰值平均值为77.61μs/ft。研究区中，各水平井的CIII岩性段导眼井段与水平井段，在水平方向的相距最大为400 m左右。在这样相距较近，分布稳定的滨岸相砂岩段的测井电性响应特征具有较好的可对比性，依然可以应用测井曲线标准化的理论和思路［14、15]。据此，作者提出了对研究区水平井声波时差曲线进行平移校正，而各井声波时差校正值，可由水平井与导眼井单井声波时差测井曲线峰值之差求得。

A井东河砂岩层段声波时差峰值为80.8μs/ft，而与该水平井段对应的导眼井段，声波时差峰值为74.6μs/ft，△AC为6.2μs/ft，因此A井的声波时差校正值为“－6μs/ft”。作者对该井声波时差曲线校正前、后进行了对比(见图2)，可以看出，校正后的声波时差曲线，与其对应导眼井的声波时差变化趋势基本一致。其余各井使用上述相同的方法，均可得到单井声波时差校正值。

图2 HD油田A井水平井声波时差曲线校正前、后对比图Fig．2 Comparison diagram of corrected acoustic log with original acoustic log of horizontal well A

通过对单井深感应、中感应电阻率频率直方图峰值的比较发现，导眼井深感应电阻率单井峰值的平均值为2.18Ω·m，中感应电阻率单井峰值的平均值为1.99Ω·m;水平井深感应电阻率单井峰值的平均值为4.2Ω·m，中感应电阻率单井峰值的平均值为3.53Ω·m。水平井的深感应电阻率和中感应电阻率，均稍高于与其对应的导眼井段的深感应电阻率和中感应电阻率，因此，需要对本区水平井的深感应电阻率和中感应电阻率进行平移校正。由于电阻率曲线具有非线性特征，各井电阻率校正系数取为导眼井与水平井单井电阻率测井曲线峰值之比值。

例如B井东河砂岩层段深探测地层电阻率峰值为5.2Ω·m，冲洗带电阻率峰值为3.3Ω·m;而与该水平井段对应的导眼井段深探测地层电阻率峰值为1.7Ω·m，导眼井段冲洗带电阻率峰值为1.18Ω·m，即有RT导眼/RT水平为0.3、RXO导眼/RXO水平为0.36。因此B井的深探测地层电阻率校正系数为“0.3”，冲洗带电阻率校正系数为“0.36”。对该井深探测地层电阻率和冲洗带电阻率校正前后进行对比(见图3及图4)，可以发现，经过校正后的水平层段内电阻率趋势值，与导眼井同一层段内电阻率趋势值基本重合。其余各井亦使用相同的方法，即可得到各水平井东河砂岩段深感应电阻率和中感应电阻率的校正系数。

通过应用程序APP可以帮助学生对日常体育基本知识作出一个基本的检测，学生通过自己的账号登录相关的平台，进入相应的网上考试窗口，进行学识自检。

图3 B井水平井电阻率校正前、后对比图Fig．3 Comparison diagram of corrected deep induction resistivity logwith the original log of horizontalwell B

图4 B井水平井冲洗带电阻率校正前、后对比图Fig．4 Comparison diagram of corrected flushed zone resistivity log with the original log of horizontal well B

通过单井同层段自然伽玛频率直方图峰值比较，导眼井自然伽玛单井峰值的平均值为35.4(API)，水平井自然伽玛单井峰值的平均值为32.5(API)，水平井自然伽玛曲线与导眼井的自然伽玛曲线值基本接近。因此，作者对本研究区内水平井的自然伽玛曲线未进行校正。

2 水平井测井储层参数解释

研究地区水平井皆未取芯，因此作者以直井岩芯物性刻度测井曲线，建立了水平井的孔隙度、渗透率神经网络解释模型，并对研究区七十八口水平井进行了储层参数计算。用直井岩芯物性资料对水平井储层参数解释结果加以检验，解释精度得到了明显改善和提高。

2．1 建立水平井神经网络孔隙度解释模型

根据水平井具有的测井曲线系列，选取自然伽玛、深感应电阻率、中感应电阻率以及声波时差，作为网络输入曲线。将选取的十九口取芯井中的764个样本，建立神经网络孔隙度计算模型。经过网络学习、训练，当隐层单元为7时，训练误差达到最小。因此，可以确定孔隙度计算模型的神经网络模型结构为4－7－1。当学习训练完毕后，可获得岩心分析孔隙度与网络预测孔隙度相关系数达到0.89(见图5)，因而达到了较高的建模精度。

图5 岩芯分析孔隙度与网络预测孔隙度交绘图Fig．5 The crossplot of core analyzing porosity versus predicting porosity with neural networks

2．2 建立水平井神经网络渗透率解释模型

根据水平井测井曲线系列，作者选取了自然伽玛、深感应电阻率、中感应电阻率、声波时差以及网络预测孔隙度等五条曲线，作为渗透率网络模型的输入曲线。使用选取的十九口井中的764个样本，建立神经网络渗透率计算模型。经过网络学习、训练，当隐层单元为5时，训练误差达到最小，因此建立渗透率计算模型的神经网络模型结构为5－5－1。从岩芯分析渗透率与网络预测渗透率交绘图(见图6)上可见，二者的相关系数R达到0.85。

2．3 水平井储层参数处理解释

3 解释效果检验

图6 岩芯分析渗透率与网络预测渗透率交绘图Fig．6 The crossplot of core analyzing permeability versus predicting permeability with neural networks

图7 HD74水平井东河砂岩段储层参数解释成果图Fig．7 The interpretation result of reservoir in Donghe sandstone section of horizontal well HD74

由于研究区内各水平井均未取岩芯，如何检验测井储层参数计算结果的可靠性和精度，是一个十分困难的问题。作者在本研究中提出，基于直井岩芯分析孔隙度、渗透率，建立水平井的神经网络储层参数计算模型。直井的岩芯分析孔隙度及渗透率，就是检验水平井测井储层参数计算结果的唯一依据。因此为了便于检验，应首先对水平井进行水平井的井深校直，然后将水平井校直后的测井曲线，与直井测井曲线进行对比。水平井在测井的过程中大多存在深度记录上的偏差，校直后的水平井测井曲线与相对应的导眼井段，在深度上仍有较大的差异(见图8)。因此，要以自然伽玛曲线为基准，对水平井校直后的井深进行垂向上、下移动。

如图8(a)为HD25H井水平井校直后与对应导眼井测井曲线。从图8(a)中明显看出，水平井校直后的东河砂岩段，与导眼井对应的井段在深度上有很大的差异。自然伽玛曲线能够识别东河砂岩段，该井水平井校直后东河砂岩的顶界面深度为5 078.125 m，该点对应的导眼井深度为5 060 m，因此对水平井校直后的深度上移18.125 m得到图8(b)。为了便于检验，可用以上的方法对其余对应导眼井有取芯的水平井，都进行深度校正(见下页图9、图10)。

在图8(b)中，HD25H井的5 062 m～5 064 m水平井段的预测孔隙度、渗透率，与直井岩芯分析孔隙度、渗透率的变化趋势基本吻合。而上段5 060 m～5 062 m水平井的预测孔隙度、渗透率，与对应直井井段的孔隙度和渗透率也基本吻合。

图9(见下页)为HD44H井水平井与导眼井储层参数测井解释成果对比图。从图9中可以看出，该井在5 078 m～5 080.5 m段的水平井预测孔隙度、渗透率，与直井岩芯分析孔隙度、渗透率有较好的吻合性。而该井的5 081 m～5 084 m段，由于受水平井声波时差曲线异常的影响，此水平井段计算出的孔隙度和渗透率可靠性较差。

图10(见下页)为HD2H井水平井与导眼井测井解释成果对比图。从图10中可以看出，该井下部的5 048.5 m～5 049.5 m段的水平井预测孔隙度、渗透率，与直井岩芯分析孔隙度、渗透率的变化趋势基本一致。而上部的5 046.5 m～5 048.5 m虽然没有岩芯物性分析值，但该井段水平井的预测孔隙度、渗透率，与对应导眼井段的预测孔隙度、渗透率曲线吻合性较好。

图8 HD25H井水平井校直移动前后测井曲线对比图Fig．8 Comparison diagram of log before or after shifting of horizontalwell HD25H

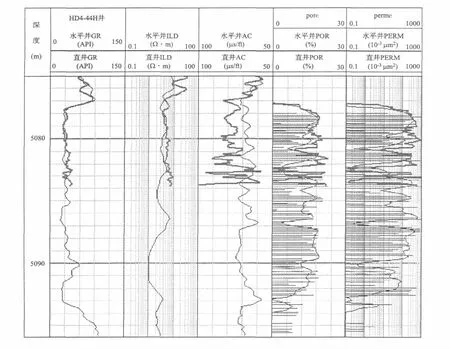
图9 HD44H井水平井与导眼井测井解释成果对比图Fig．9 Comparison diagram of log interpretation result of horizontal well HD44H vs．pilot hole well

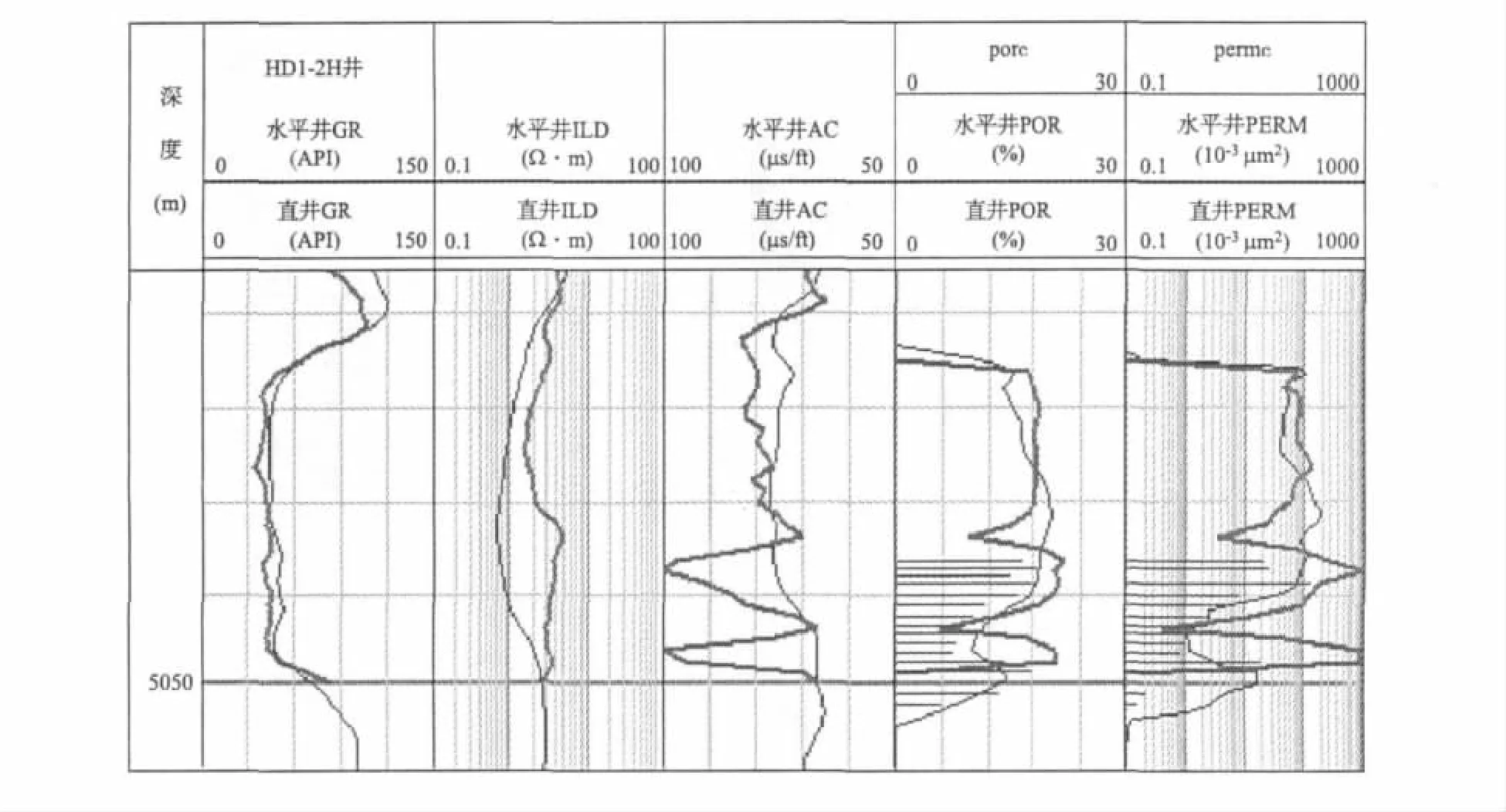
图10 HD2H井水平井与导眼井测井解释成果对比图Fig．10 Comparison diagram of log interpretation result of horizontalwell HD2H vs．pilot hole well

4 结论

(1)作者在文中归纳总结了HD油田水平井东河砂岩段的测井响应特征，提出了水平井储层参数神经网络测井定量解释流程和解释结果有效性的检验方法，获得了较高的储层参数计算精度。同时，作者还对研究区内七十八口水平井的孔隙度、渗透率等储层参数，进行了计算和评价，能够较好地满足本区三维地质建模井属性参数精度要求。

(2)东河砂岩水平井声波时差测井曲线值，高于直井对应层段的声波测井曲线值，电阻率测井值亦高于直井对应层段的电阻率测井值。根据水平井与对应直井井段的测井曲线特征，作者对水平井声波时差与电阻率曲线进行了平移、伸缩校正，并将利用直井岩芯分析建立的储层参数计算模型，用于水平井的储层参数解释中，取得了较高的精度和较好的效果。

(3)作者本次研究的水平井测井曲线校正方法，适用于井眼较规则、水平井轨迹准确、砂岩电性响应特征明显等情况。而对于井眼轨迹不清及复杂岩性的井段，尚需进一步研究出其它克服这种会出现较大差异曲线情况下水平井段测井储层参数解释的有效方法。

［1]MORAN JH，GIANZERO S．Effects of formation anisotropy on resistivity logging measurements［J]．Geophysics，1989:44．

［2]李厚裕，刘呈冰．水平井测井解释原理与应用［M]．北京:石油大学出版社，1993．

［3]李谦 ，李庆合 ，马建英，等．水平井测井评价技术在大港油田的应用［J]．测井技术，2008，2(5):455．

［4]徐建华，陈小斌，唐开宁，等．水平井中双侧向测井的侵入校正［J]．测井技术，1996(2):113．

［5]KLEIN JD．Induction log anisotropy corrections［J]．The Log Analyst，1993，34(2):18．

［6]赵江青，王成龙，叶青竹．岩石各向异性在水平井测井解释中的应用［J]．测井技术，1998，22(1):36．

［7]刘呈冰，李厚裕．水平井咨询系统在胜利油区的应用与发展［J]．测井技术，1994，18(1):30．

［8]赵军，海川．水平井测井解释中井眼轨迹与油藏关系分析技术［J]．测井技术，2004，28(2):145．

［9]易觉非．水平井井眼轨迹解释软件系统设计［J]．长江大学学报:自科版，2006，3(1):77．

［10]李鹏翔，林静．水平井测井解释研究的发展［J]．江汉石油学院学报，1999，21(2):23．

［11]周灿灿，王昌学．水平井测井解释技术综述［J]．地球物理学进展，2006，21(1):152．

［12]焦翠华．塔里木盆地哈得4油田东河砂岩层序地层界面类型及测井识别方法［J]．石油与天然气地质，2007，28(1):69．

［13]杨斌，刘晓东，徐国盛．川东沙罐坪石炭系气藏测井储层评价［J]．物探化探计算技术，2010，32(1):35．

［14]杨斌，匡立春．神经网络及其在石油测井中的应用［M]．北京:石油工业出版社，2005．

［15]谭茂金．测井数据标准化方法研究及软件设计［J]．物探化探计算技术，2006，28(3):219．

TE 122.2+3

A

1001—1749(2011)02—0195—07

2010－09－27改回日期:2010－12－08

杨斌(1967－)，男，汉族，山东宁阳人，博士，教授，主要从事地球物理综合解释，油气田开发地质工作。