基于研发型项目区间算法的进度计划方法研究

欧立雄，陈照鲁

(西北工业大学管理学院，西安710129)

引言

区间算法最早由摩尔(R.E.Moore)于20世纪50年代末提出，区间算法主要通过定义一系列在区间上的运算法则如区间加法、区间减法、求最大、最小值等运算来进行区间上的运算，其初衷是为了提高计算结果的可靠性。一开始主要运用于取代浮点算法运用于计算机的数字存储方面。例如一个实数x，在计算机中实际上是用一个区间［］来表达的。区间算法与传统的算法有着不同的性质，区间算法的加减法是不可逆的即:A+B-B≠A。区间本身具有集合的属性，区间之间可以进行集合运算，而且实践中许多参数也只能用区间来表示。许多基于区间算法的新的计算方法能够可靠地解决一些传统方法难以解决的问题。如:求解非线性方程组在指定区域内的所有数值解。

对于研发型项目，由于其工序工期具有很大的不确定性，有些工序只能大概知道一个可能的工期区间。面对这样的问题，有学者提出模糊关键路径法［1］来对这一类型的项目进行计划和控制。这种方法在计算各工序的最早开始时间、最迟时间和松弛时间时，使用了模糊减法运算［1］，很好地解决了研发型项目中工序时间不确定性较大的问题，但这样的模糊减法运算在某些情况下，其减法的结果可能为负值，这一现象的存在使模糊运算失去了意义。为了解决这一难题，学者Chanas在其论文中［3～5］给出了区间工期的网络图关键路径和关键工序的定义及判定定理，并进一步证明了判定某一工序的可能关键性是一个NP完全问题，计算给定工序的浮动时间界限是NP难的(和求解 NP完全问题一样困难)。另外，Dubois在其论文中［6］提出了计算区间工期的串—并网络图的时间参数启发式算法，并将其推广到模糊计划网络中。Zielinki也在其论文中［7］给出了区间工期的一般性网络图中计算时间参数的算法，并提出通过浮动时间的值来判别工序是否关键的思想。该类方法一定程度解决了研发型项目面对工序工期不确定时的计划制定问题，但目前仍存在着算法复杂度高，浮动时间计算不精确等问题。

目前存在的区间算法里其基本思想是在定义了相应的区间算法后，类比传统的CPM的方法来计算项目网络图中各个工序及节点最早开始时间、最迟开始时间。在用逆推法求取工序的最迟开始时间时，因为对项目工序的取值区间没有必要的限定，这样如果某一个或几个工序的工期取值区间过大，就很有可能会出现运算结果为负值的情况。而且过大的工序工期取值区间会使最终求得的项目完工时间区间也变得非常大，这样运算结果也就相应的没有什么意义。因此本文同样在已有的区间算法的基础上进一步增加限定条件，要求网络图中每一个工序其工期的估计区间的跨度不超过其区间的下界。即对工序工期的估计要求一定的精度。如工序区间［3 6］在本方法中是可以接受的估计精度。而工序区间［3 7］是不可以接受的估计精度。并在用逆向递推法计算工序最迟开始时间下界时进行必要的修正，来抵消因为区间减法的一直进行而使运算结果不断变小甚至变成负值的趋势，这样再通过增强条件要求就可以有效地避免在用逆推法求取工序最迟开始时间区间时出现的令整个算法失效的负值。

一、算法的基本思想

本算法主要是在传统的关键路径法的思想基础上发展而来，类比传统关键路径法求取网络图中各工序及节点的最早开始时间、最迟开始时间的思想，通过定义一系列在区间上的加减法、求取最大值最小值的运算，来求取网络图中各工序和节点的最早和最迟开始时间区间。本算法也是采用从前向后递推的方式求取网络图中各工序和节点的最早开始时间区间，然后网络图中终点的最迟开始时间区间等于其最早开始时间区间，则该项目的结束时间区间就是其终点的最早开始时间区间。再由后向前递推，求取网络图中各工序和节点的最迟开始时间区间。然后，由工序的最早开始时间区间和最迟开始时间区间来求取网络图中各个工序的松弛时间的上限和下限，再由各个工序的松弛时间的上限和下限是否为零来判断该工序的可能关键性。当找到一条从始点到终点的路径，该路径上所有的工序都为关键的，则该路径就是关键路径。

二、基于区间算法的进度计划方法的定义

本方法研究的研发型项目其网络图也必须是一个有向、紧凑、无环的网络图。且只有一个起点和终点。且该网络图中各个工序的工期具有区间活动周期。记网络的开始点为O，结束点为V，网络中的节点数为n。记字母i、j、k分别表示网络图中任意一个节点。因为对于网络图其始点和终点的最早开始时间和最迟开始时间是相等的。因此在下面的讨论中不再讨论始点和终点的情况，即:

本方法研究的具有区间活动周期的项目可以表示为一个有向无环图S=(A，D).其中，N={l，2，…，n)为结点集合，A=N X N 是有向弧(工序)集合，S中只有一个始结点O和一个终结点V.对于活动(i，j)∈A，有i＜j。每个活动(i，j)∈A的工序工期区间为(i，j)≥0。

B(i)表示节点i的紧前节点的集合(before);

S(i)表示节点i的紧后节点的集合(successor event);

d表示工序某一工期t(i，j)∈T(i，j)的一个环境，tij(d)表示活动(i，j)在环境d下的精确活动周期;

R是工序的所有可能工期的环境集合，为区间数T(i，j)的笛卡尔积;

Cij为从结点i到结点j的所有路径的集合(链条:chain);

Tc(d)表示某一路径c在配置d下的路径长度;

用ES(i，j)表示工序(i，j)的最早开始时间区间;

用LS(i，j)表示工序(i，j)的最迟开始时间区间;

定义图形●为区间上的加法运算，定义图形▲为区间上的减法运算，定义MAX以及MIN在此处表示为区间数的取最大值和最小值的运算(完全不同于原来实数域上的运算)。

三、基于区间算法的进度计划方法

类比传统的网络图中工序最早开始时间和最迟结束时间的求法可知:采用从前向后的递推方式可求得各活动和结点的最早开始以及最早结束时间区间。采用从后向前的逆推方式可求得各活动和结点的最迟开始以及最迟结束时间区间。

具有区间活动周期的网络图中对于任意一个节点i，其最早开始时间ES(i)为:

其中k∈B(i)。

具有区间活动周期的网络图中任意一个节点i最早开始时间区间计算公式为:

其中k∈B(i)。

具有区间活动周期的任意一个工序(i，j)最早开始时间区间计算公式为:

其中k∈B(i)。

具有区间活动周期的工序(i，j)最迟开始时间区间计算公式为:

记在某一环境下活动(i，j)的最迟开始时间为 ls(i，j):

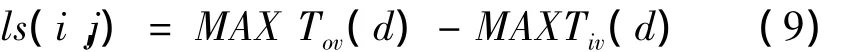
1.对于任意一工序(i，j))的最迟开始时间的上界为:

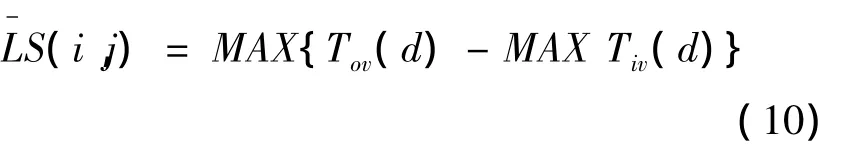
其中此处的MAXR运算为新定义的一种算法。MAX(A-B)表示分别从区间A和B中任取两个数x、y，然后对x和y的全部可能性差值的求最大运算，其中A、B表示两个区间。

3.如果对于任意一工序(i，j))的最迟开始时时间的下界为:S(i，j)，那么对于节点i的最迟开始时时间的下界为:

4.如果对于任意一个节点i，记其最迟开始时间的下界为 L-S(i)=X，最早开始时间下界S(k)=Z，工序(k，i)的工期周期的上界i)=y那么对于工序(k，i)其最迟开始时间的下界为:

5.如果工序(i，j)的最迟开始时间为LS(i，j)，记所有以节点i为起点的工序的集合为M，记所有以节点i为起点的工序的最迟开始时间区间的集合为X，则对于节点i，其最迟开始时间的上界为:

其中内层的MIN表示对所有过i节点的工序的最迟开始时间区间的求最小值运算。外面的max表示对区间{MI N(ij)∈M{X}}的求最大值。

7.一个工序(i j)为关键工序当且仅当其松弛时间的上界界(i，j)=0。

9.一个工序(i j)为可能关键工序当且仅当其松弛时间的下界T(i，j)=0。

通过上面判定1到10为基础，本算法的步骤可表述如下:

步骤一:根据工序间的逻辑关系画出项目的网络图，并估计各个工序的工序取值区间。

步骤二:根据公式(6)、公式(7)由前往后递推各个节点和工序的最早开始时间的区间。

步骤三:列出网络图中所有从始点到终点的路径。

步骤四:根据判定1、判定4和判定3、判定5以及公式(8)、公式(9)、由后向前递推网络图中各节点和工序的最迟开始时间区间。

步骤五:根据判定2计算出各个工序松弛时间的上界。

步骤六:根据判定6计算出各个工序松弛时间的下界。

步骤七:判断各个工序和始点到终点的路径的可能关键性，并给出项目的结束时间区间。

四、模型验证

笔者将以某一具体的项目为例通过利用本算法求取该项目网络图的完工时间区间以及可能关键路线来验证该算法的有效性。

已知该项目的工序工期区间以及工序的紧前、紧后关系如表1所示:

表1 工序工期及其相互间的逻辑关系

步骤一:记项目始点为O，终点为V。根据项目工序关系表画出项目网络图，如图1所示:

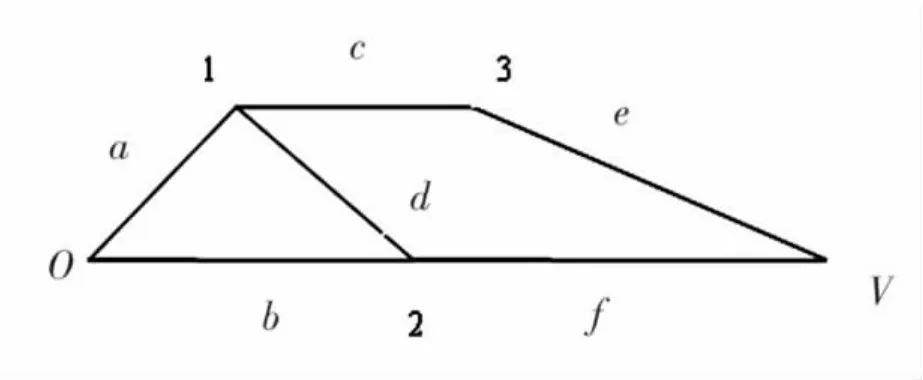
图1 项目网络图

步骤二:类比工期固定的网络图中求解节点最早开始时间的方法(CPM)运用公式(6)求解网络图中各节点的最早开始时间区间(以下为了简便起见，不再给出具体的运算过程，仅仅为了验证算法的需要给出最后的计算结果)。网络图中各节点的最早开始时间区间为:

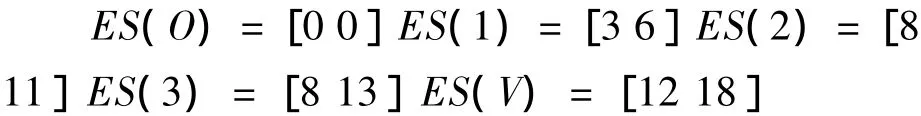
网络图中各工序的最早开始时间区间为:

步骤三:网络图中所有从始点到终点的路径有

a-c-e a-d-f b-f三条路径。

步骤四:网络图中各个节点的最迟开始时间区间为:

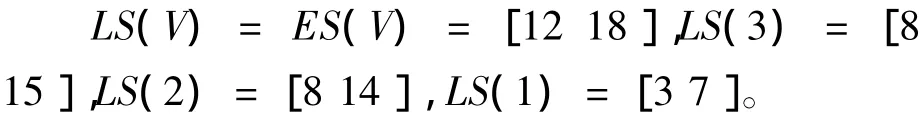
网络图中各个工序的最迟开始时间区间为:

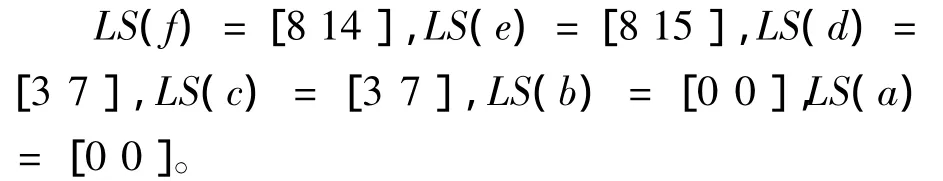
步骤五:计算各个工序的松弛时间下界，根据判定六可知:本网络图中所有工序的松弛时间的下界全为0。

根据判定2求各个工序的松弛时间上界为:

步骤六:

根据判定7可知工序a、b为关键工序。

根据判定8可知该网络图不存在关键路径。

根据判定9可知该网络图的可能关键工序为c、d、e、f。

根据判定10可知该网络图的可能关键链为:a-c-e a-d-f b-f三条可能关键路径。该项目的完工时间区间为［12 18］。

五、结论

通过实例计算，可以看出该文提出的基于区间算法的项目进度计划方法可以较好地解决工序工期为区间类型的不确定型的项目的网络进度计划的制定问题。对于一些较为简单的工序工期不确定型的网络图，该方法求解效率很高，对于项目规模较大的此类问题，可根据上述算法步骤编制相应的计算机程序进行求解，由于本文提出的算法主要利用工序间的紧前紧后关系，采用了层层递推的算法，对于层层递推的算法，用计算机编程是很容易实现的。综上所述，本文提出的基于区间算法的项目计划方法能够有效求解实际中项目工序工期为区间类型的不确定性的项目计划调度问题，具有一定的理论与实际应用价值。

［1］伊长生.不确定环境下研发项目的决策分析［D］.天津:天津大学2006.12.

［2］张宏国，徐晓飞，战德臣.具有不精确活动周期的网络计划方法［J］自动化学报，2008，34(9):1178-1184.

［3］Chanas S，Zielinki P，Critical path analysis in the network with fuzzy activity times［J］.Fuzzy Sets and Systems，2001，122(2):195-204.

［4］Chanas S，Zielinki P，On the hardness of evaluating criticality of activities in a plannar network with duration intervals［J］.Operations Research Letters，2003，31(1):53-59.

［5］Chanas S，Dubois D，Zielinki P.On the sure criticality of tasks in activity networks with imprecise durations［J］.IEEE Transactions on Systems，Man，and Cybernetics，Part B:Cybernetics，2002，32(4):393-399.

［6］Dubois D，Faddier H，Galvagnon V，On the latest starting times and floats in activity networks with ill-known duration［J］.European Journal of Operational Research，2003，147(2):266-280.

［7］Ziizika P.On computing the latest starting times and floats of activities in a network with imprecise durations［J］.Fuzzy Sets and Systems，2005，150(1):53-76.

［8］A.F.Carazo，Trinidad Gómez，Julián Molina，Alfredo G.Hernández-D íaza， FlorM.Guerreroa， Rafael Caballerob.Solving a comprehensive model for multiobjective project portfolio selection18［J］.Computers ＆Operations Research，2010，37:630-639.

［9］JoséAlberto Araúzo，Javier Pajares，Adolfo Lopez-Paredes Simulating the dynamic scheduling of project portfolios.Simulation Modelling Practice and Theory［J］.Simulation Modelling Practice and Theory.2010，18:1428-1441.

［10］Senay Solak ，John-Paul B.Clarke ，，Ellis L.Johnson，Earl R.Barnes.Decision Support Optimization of R＆Dproject portfolios under endogenous uncertainty［J］.European Journal of Operational Research.2010，207:420-433.

［11］Qi Hao ，Weiming Shen，Yunjiao Xue，Shuying Wang.Task network-based project dynamic scheduling and schedule coordination.Advanced Engineering Informatics.2010，24:417-427.

［12］Moore R，Yang C.Interval Analysis［R］，Technical Document，Lockheed Missiles and Space Division，Number LM SD-285875，1959.

［13］Moore R.Methods and Applications of Interval Analysis［M］. Society for industrial and Applied Mathematics，1979.