模糊自适应PID控制方法研究与仿真

李春光,孙朝霞

(厦门理工学院计算机科学与技术系,福建厦门 361024)

模糊自适应PID控制方法研究与仿真

李春光,孙朝霞

(厦门理工学院计算机科学与技术系,福建厦门 361024)

对于非线性、时变性的系统来讲,传统PID控制难以达到满意效果。利用模糊推理的方法实现对PID参数的在线自动整定,并且在Matlab软件环境下进行了研究与仿真。仿真结果表明,参数自适应模糊PID控制能使系统控制响应快、控制稳定,且具备了良好的动态性能。

模糊自适应;PID控制;Matlab仿真

在许多实际的工业过程中,由于普遍存在的非线性、参数时变性和模型的不确定性,使得常规的PID控制难以取得预期的效果。而模糊控制对数学模型的依赖性弱,不需要建立过程的精确数学模型,只要把模糊规则以及评价指标、初始PID参数等作为知识存入知识库中,即可根据控制系统的实际情况,通过知识及模糊推理实现对PID参数的最佳调整。这样既实现了PID控制的高精度,又具有了灵活性和自适应性,是解决实际系统控制问题的有效途径。采用Matlab仿真器对模糊自整定PID参数控制系统进行仿真,可快速、方便地验证各种规则和参数的有效性。

1 模糊自适应PID控制方法的原理

过程控制中的常规PID控制算法具有计算量小、实时性好等优点[1]。如果针对控制过程建立了适当的数学模型,只要设置KP、KI、K D这几个控制参数,就可以实现PID控制的作用。但对于非线性、大延迟性等具有诸多不确定因素的系统,其控制效果欠佳。如果要应用于此类系统,则需根据不同工况对常规PID控制器的KP、KI、K D进行调整,也就是说,PID控制器要具有优良的自整定性才可以更好地运用于实际的工况。应用模糊控制算法来实现对PID参数的自动整定是一种比较有效的解决方案,即利用模糊推理规则,用实测值与设定值间的误差以及误差变化率作为系统的输入,对PID调节器的KP、KI、K D参数进行调整,从而实现对控制对象的实时控制[2]。其控制系统结构图如图1所示。

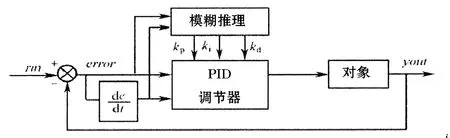
图1 模糊自适应PID控制器结构图

2 模糊自适应PID控制方法的实现

模糊PID控制器系统的核心是模糊推理器,它决定了控制系统的精确性[3]。模糊推理器的功能是在系统运行过程中找出PID调节器的输入KP、KI、K D与误差e及误差变化率ec之间的模糊关系,并且在系统运行过程中,不断检测误差e与误差变化率ec,根据模糊控制策略对KP、KI、K D进行在线修正,从而满足不同控制环境变化的需求,以获得良好的响应控制和动态控制性能。

2.1 模糊推理器的结构

如模糊控制系统机构图1所示,将误差e和误差变化率ec作为模糊推理器的两项输入参数、将三个参数KP、KI、K D作为控制器的输出,提供给PID调节器,作为PID的在线修正参数。

2.2 模糊推理器的隶属度函数

设E为输入误差e的语言变量,EC为误差变化率ec的语言变量。{-3,-2,-1,0,1,2,3}为E和EC的论域,它们的模糊子集为{NB(负大),NM(负中),NS(负小),ZO(零),PS(正小),PM(正中),PB(正大)}。KP为比例系数KP的语言变量,KI为积分系数 KI的语言变量,K D为微分系数 K D的语言变量。它们的模糊子集为{NB(负大),NM(负中),NS(负小),ZO(零),PS(正小),PM(正中),PB(正大)}。图 2,图 3,图 4,图 5 为分别为 E、EC以及三个参数的隶属函数曲线,其量化范围分别为(-013,013),(-0106,0106),(-3,3)。

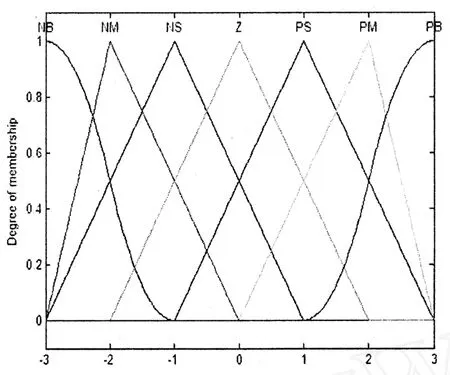
图2 误差e及变化率ec的隶属度函数

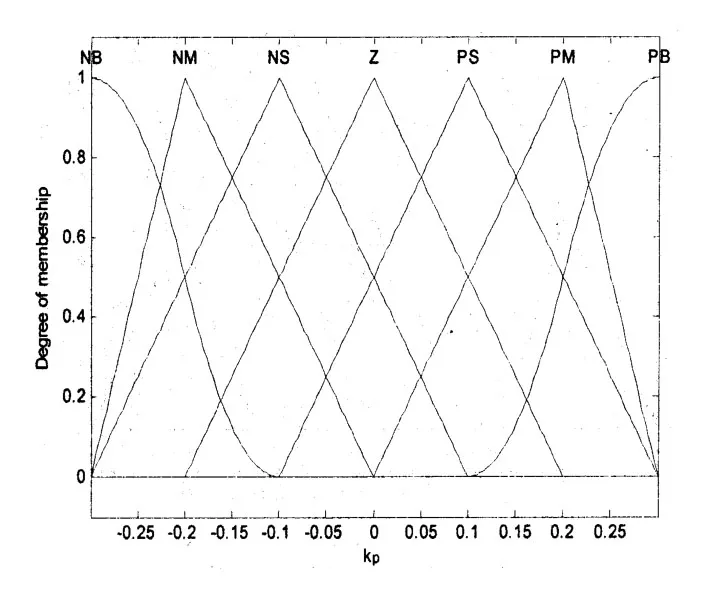
图3 KP的隶属度函数

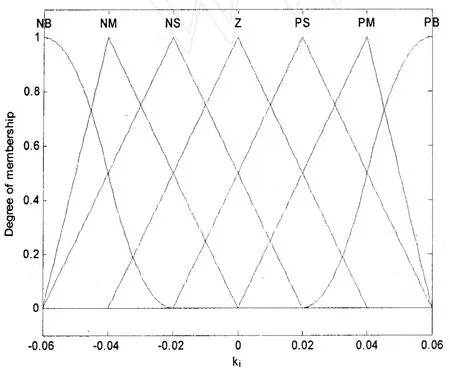
图4 Ki的隶属度函数

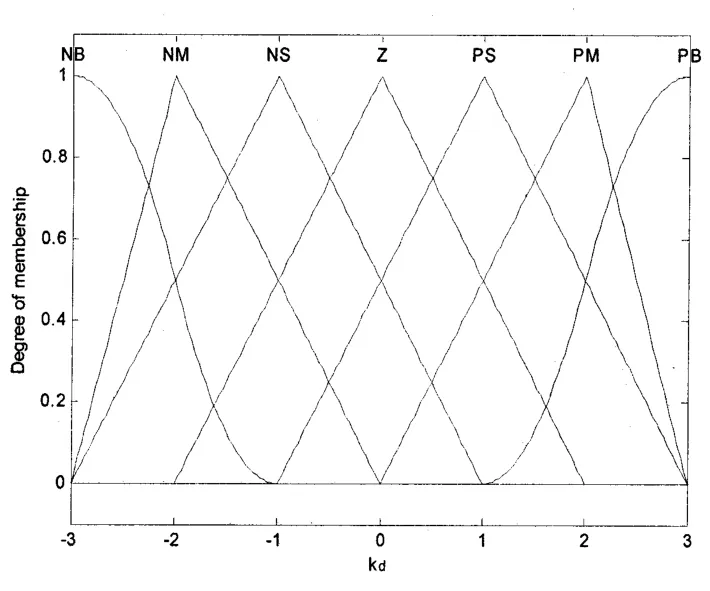
图5 Kd的隶属度函数

2.3 建立模糊控制规则

模糊控制器应首先根据专家经验知识库来建立PID的三个参数与误差e及误差变化率ec之间的模糊关系,再通过系统运行过程中不断对e和ec进行检测,由模糊控制规则对PID三个参数实行在线自适应调整[4]。

PID算法的三个参数会影响系统的稳定性、响应速度、超调量以及稳态精度[5]。在系统运行过程中对不同的误差e及误差变化率ec,参数KP、KI、K D的自适应调整规则是:(1)如果误差e较大情况,既为了加快系统的响应速度,又考虑微分过饱和而致使控制作用超出范围,应取较大的KP和较小的K D,KI一般设定为0;(2)如果误差e和误差变化率ec为中等情况时,既要保证一定的响应速度又要有小的超调量,KP和K D的取值应较小,KI一般设定为中等大小;(3)如果误差e较小情况时,为了使系统有较好的稳定性,应增大KP、KI的值,K D的值要视误差变化率ec的大小而定,ec大则K D小,ec小则K D大。

因此,要根据不同时刻KP、KI、K D这几个调节作用的强弱及协同关系来确定特定的控制规则,从而实现自动整定[6]。根据其作用原理与操作经验设定的模糊整定控制规则见表1。

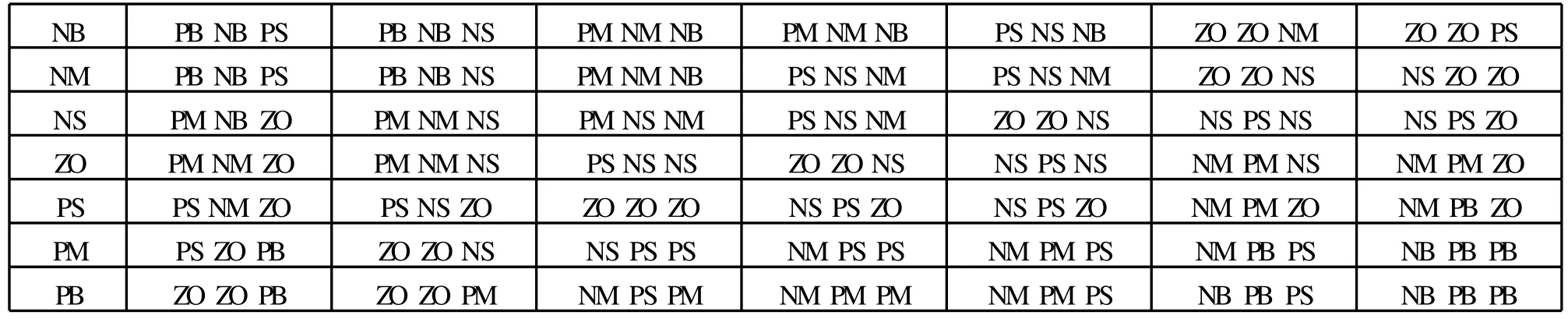
表1 模糊整定规则表

2.4 编辑模糊控制器

应用Matlab R2007中的FIS对模糊控制器进行编辑,建立FIS文件用于组建控制系统时调用。FIS文件的文件名为Fuzzpid1fis,其类型为Mamdani,推理规则为min,合成规则为max,解模糊规则为centroid,并设置二个输入以及三个输出变量。在函数编辑器窗口分别设定e、ec以及 KP、KI、K D的隶属度函数和函数的量化范围。在规则编辑窗口根据模糊整定规则表设置输入、输出变量所对应的模糊整定规则。模糊系统fuz2 zpid1fis的结构如图6。

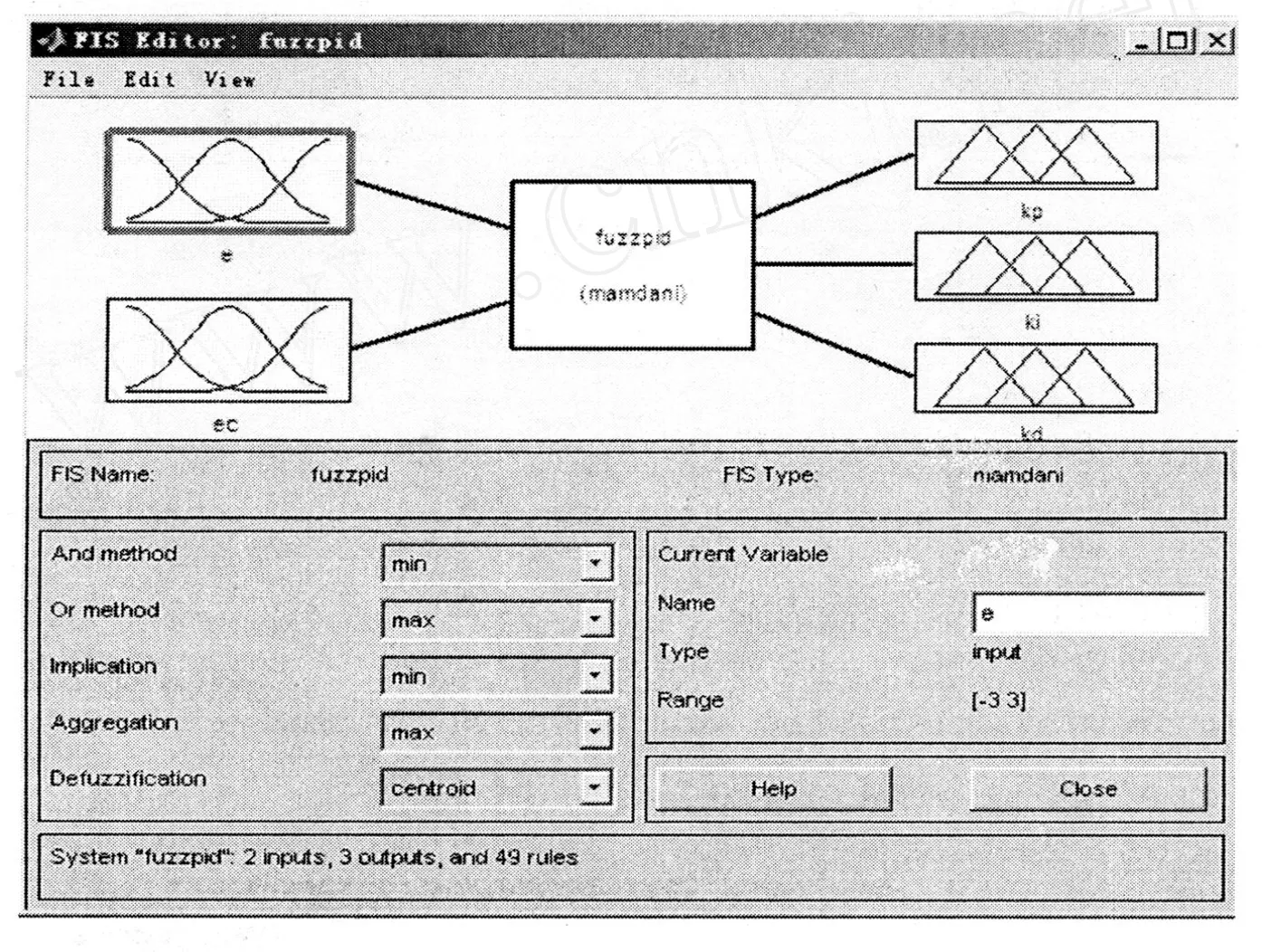
图6 模糊系统fuzzpid1fis的结构

3 应用MAT LAB对模糊自适应PID控制方法进行仿真

为了验证该方法的有效性,取某工业过程控制对象为例,其传递函数为:

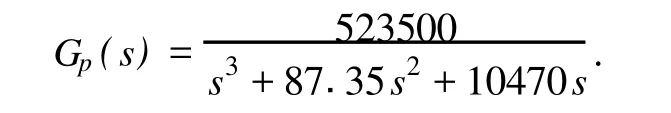
采用Matlab R2007所提供的环境进行仿真试验,输入信号为单位阶越信号,采样时间为1ms,KP、KI、Kd的初始值分别为0156,01001和01255;在FIS中设定模糊控制器的调用方法,将FLC在工作空间中输出,再由FIS文件调用。按照模糊整定规则可得KP、KI、Kd的修正值,模糊自整定控制器的实际调节量即为输入至PID的参数与初始值之和。在300ms的时候,给控制器加入一个幅度为110的干扰,其仿真控制结果与传统PID控制效果的比较见图7与图8。

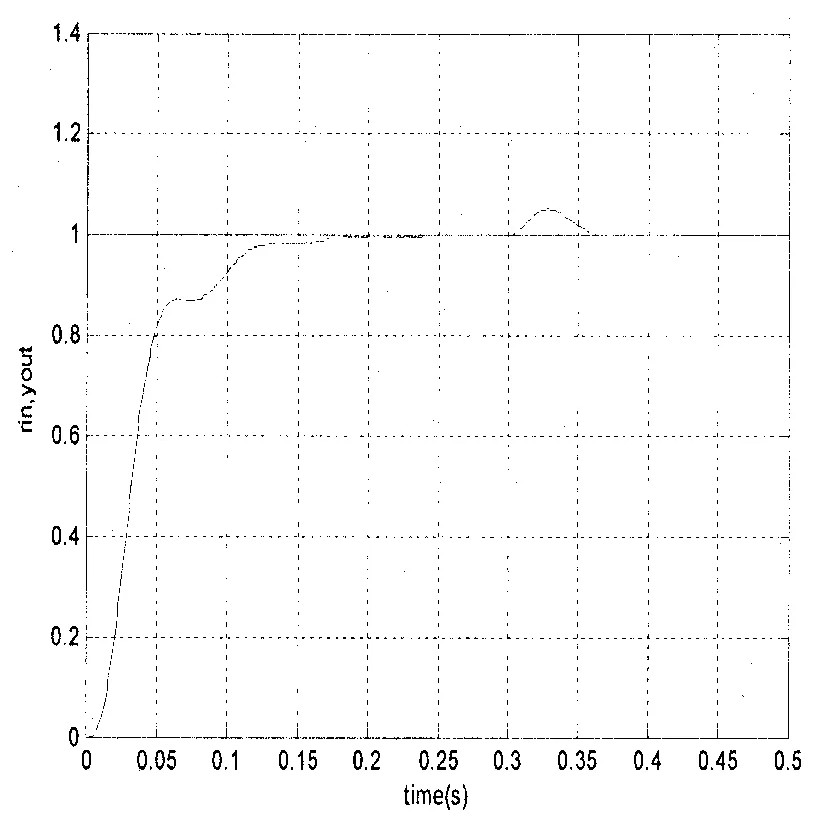
图7 传统PID算法仿真

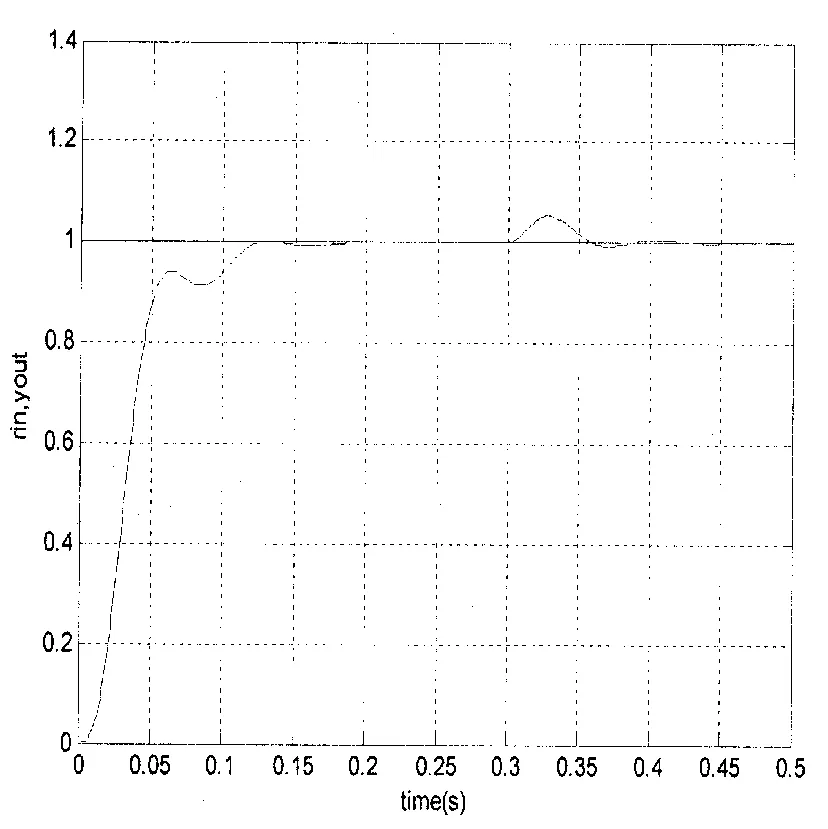
图8 模糊自整定PID算法仿真

由图8与图7所仿真的两种控制效果可见,模糊自整定控制器的响应时间短、超调量小,控制效果较好,自整定能力强。但在有外来扰动进入时有轻微的震荡,在今后的研究中仍需加以改进。

4 结语

经典控制理论中最常用到的PID控制具有原理简单、易用等优点,但如果将其用于非线性、实时性要求高的复杂系统中,效果欠佳。模糊控制算法可在传统PID控制的基础上实现模糊自整定,该技术的计算量小、灵活度高且易于实现。本研究利用Matlab R2007进行仿真试验,结果表明模糊自整定算法可以发挥传统算法与模糊控制的优点,较好地适应控制过程中被控制对象的变化以及外来的扰动。在系统参数发生改变时,具有较好的自整定能力,其控制响应时间、超调量等参数较传统PID控制效果有明显改善,这在实际的过程控制中具有参考价值。

[1]刘金馄.智能控制[M].北京:电子工业出版社,2009.

[2]陶永华,尹怡欣,葛芦生.新型PID控制及其应用[M].北京:机械工业出版社,1998.

[3]J.J.Hopfield,D.W.Tand.Neural computation of decision in optimization problems[J].Biological Cybernetics,1985,52:141-152.

[4]刘金馄.先进PID控制MAT LAB仿真[M].北京:电子工业出版社,2004.

[5]薛定宇.控制系统计算机辅助设计[M].北京:清华大学出版社,2006.

[6]廉小亲.模糊控制技术[M].北京:中国电力出版社,2003.

The Method Study and Simulation of Fuzzy Self-adaptive PID Control

LI Chun-guang,SUN Zhao-xia
(Department of Computer Science and Technology,Xiamen University of Technology,Xiamen 361024,China)

Conventional PID control can not reach a satisfactory result in nonlinear and time varying systems.In this study,a fuzzy inference method is adopted to realize the automatic regulation of PID parameters.The application of the controller in a certain system is also simulated in Matlab.The resultsof the simulation show that the fuzzy self-adaptive control has certain advantages over conventional ones in the aspects such as fast-response,high-stability and better-flexibility.

fuzzy self-adaptive;PID control;Matlab simulation

TP27312

A

1008-178X(2011)02-0045-04

2011-03-08

厦门市科技计划项目 (3502Z20093037);厦门理工学院科研启动资助项目 (YK J06003R)。

李春光 (1967-),男,辽宁营口人,厦门理工学院计算机科学与技术系副教授,硕士,从事智能控制、嵌入式测控研究。