高压管路透镜垫连接件结构分析

闫 峰，赵宏轩，余爱英

（西安航天动力试验技术研究所，陕西西安710100）

0 引言

液体火箭发动机由推力室、涡轮泵、燃气发生器、阀门和调节器等组合件构成，组合件试验成为发动机研制工作的重要组成部分。某试车台设计用于发动机高压组合件试验，该试车台的增压系统管路和部件连接采用了透镜垫和锥面连接的连接密封结构。拧紧力矩过大可能会导致螺栓拧断，透镜垫－锥面被压碎、扭曲或断裂，也可能使螺纹牙被剪断而脱扣，最终影响密封质量。

本文主要通过连接结构力学分析进行了密封计算和螺栓强度校核，并在此基础上用有限元分析软件ANSYS对密封结构进行接触分析，得出了透镜垫－锥面结构在不同拧紧力矩作用下的受力状况，为确定拧紧力矩与透镜垫－锥面的接触应力及接触面积的关系及进行力学环境试验研究提供必要的参数。

1 连接结构力学分析

在系统管路装配过程中，透镜垫球面和螺纹接管锥面结构在螺母拧紧力矩T的作用下，锥面和球面承受轴向预紧力F，表面之间逐渐旋合接触压紧，形成接触面实现密封，连接结构如图1所示。本文选取通径DN65的连接结构进行结构分析和接触分析。

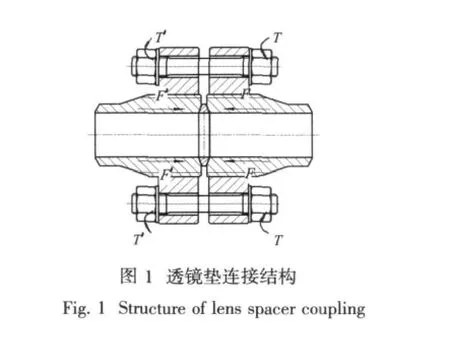
1.1 密封计算

通过比较密封面计算比压和必须比压，对透镜垫连接结构进行密封计算。高压气体管路设计压力为45 MPa，透镜垫和螺纹接管材料为0Cr18Ni10Ti。

密封面上的总作用力：

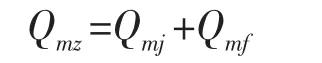
Qmj为密封面上的介质作用力：

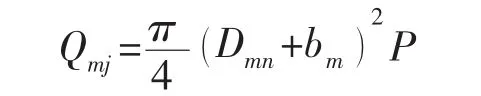
式中：Dmn为密封面内径，Dmn＝Dk－bm，其中Dk为圆直径，，其中，R为球半径，θ为锥角；p为设计压力；bm为密封面宽度，bm＝α为接触半角，β为摩擦角，F为螺栓所受总轴向力，E为材料弹性模量。Qmf为密封面上密封力：

式中，Dmw为密封面外径；Dmw=Dk+bm；qmf为密封面上必须比压；

要保证结构密封，密封面计算比压q应大于qmf，其中，密封面计算比压：

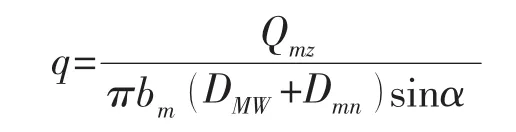
代入各参数，计算结果为：q=258 MPa＞qmf=132 MPa。因此，透镜垫连接结构可以保证在设计压力下的密封性。

1.2 螺栓强度校核

通过比较实际螺栓面积和需要的螺栓面积，对螺栓进行强度校核。螺栓材料：0Cr18Ni10Ti，螺母材料：2Cr13。

螺栓载荷为：

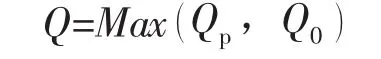
式中：Qp为工作状态下需要的最小螺栓载荷

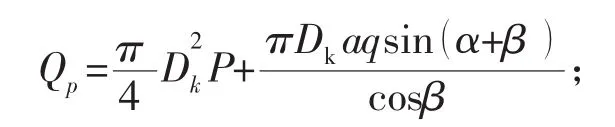
Q0为预紧状态下需要的最小螺栓载荷

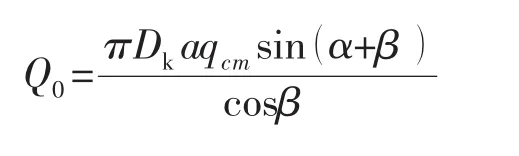
式中：qcm为预紧比压；q为最大密封比压；a为接触面宽度。需要的螺栓面积：

式中：A1为预紧状态下需要的最小螺栓面积，为常温下螺栓材料的许用应力；A2为工作状态下需要的最小螺栓面积，为设计温度下螺栓材料的许用应力。

要保证螺栓强度要求，应保证：实际螺栓面积A大于需要的螺栓面积上式中，A=SZ，（S为单个螺栓面积，其中d2为螺纹小径；Z为螺栓个数）。

代入各参数，计算结果为：A=3600 mm2＞Am=2484 mm2。所选用的螺栓满足透镜垫连接结构在工作状态下和预紧状态下的强度要求。

2 透镜垫密封数值分析

2.1 接触分类

接触问题是一种高度非线性行为，为了进行有效计算，必须正确理解问题的特性并建立合理的模型。接触问题分为两种基本类型：刚体与柔体的接触；半柔体与柔体的接触。在刚体与柔体的接触问题中，接触面的一个或多个被当作刚体，一般情况下，一种软材料和一种硬材料接触时，问题可以被假定为刚体与柔体的接触，许多金属成形问题归为此类接触；另一类，柔体与柔体的接触，是一种更普遍的类型，在这种情况下，两个接触体都是变形体。

2.2 ANSYS接触能力

ANSYS支持三种接触方式：点与点，点与面，平面与面，每种接触方式使用的接触单元适用于某类问题。为了给接触问题建模，首先必须认识到模型中的哪些部分可能会相互接触，如果相互作用的其中之一是一点，模型的对应组元是一个结点。如果相互作用的其中之一是一个面，模型的对应组元是单元，例如梁单元，壳单元或实体单元，有限元模型通过指定的接触单元来识别可能的接触匹对，接触单元是覆盖在分析模型接触面之上的一层单元。

透镜垫密封结构是由螺纹接管锥面和透镜垫球面构成的密封结构，属于面与面的接触分析。其中，螺纹接管锥面边界作为“目标”面，而把透镜垫球面作为“接触”面，“目标”面总是刚性的，“接触”面总是柔性面，这两个面合起来作为一个“接触对”。

2.3 接触分析步骤

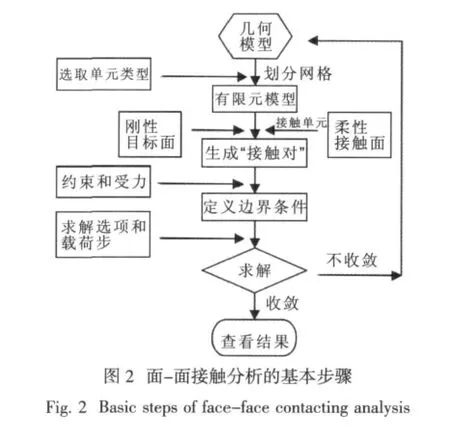
一个典型的面与面接触分析的基本步骤如下图所示，主要包括：

1）建立模型，划分网格，得到有限元模型；

2）定义刚性目标面、柔性接触面，生成“接触对”；

3）按照约束和受力情况，定义边界条件；

4）对接触问题进行求解，若不能收敛，检查模型各种设置再重新进行求解；

5）若求解收敛，则可通过后处理器或时间历程后处理器查看位移、应力、应变，支反力和接触信息（接触压力、滑动等）等计算结果。

2.4 透镜垫密封接触分析

对于接触单元来说，有限元计算网格中每个单元包含应力、应变、位移等力学参数，因此可通过统计实际参加接触的单元的位置参数得出透镜垫－锥面密封面的实际状态。通过求它们的接触应力的平均值，可以得出接触面的平均接触应力；通过计算它们在锥面切向的密封长度可以得出密封宽度，将密封宽度乘以密封环中间段周长，可以得出整个接触面的密封面积。

考虑到计算机的资源和运算效率，并根据透镜垫连接件结构的几何对称特点，只对其中一侧的密封结构进行建模，几何模型如图3a。其中，模型包括透镜垫的一半，以及与其接触的螺纹接管一个。采用ANSYS单元库实体单元SOLID185进行网格划分，共得到4612个节点，19308个单元。有限元模型如图3b。

将螺纹接管锥面定义刚性目标面，透镜垫球面定义柔性接触面，球面-锥面构成接触对，接触面如图4a所示。按照连接结构的实际工作过程，设定透镜垫剖面为全约束，将螺栓拧紧力矩转化为作用在螺纹接管端面的均布力，边界条件如图4b所示：

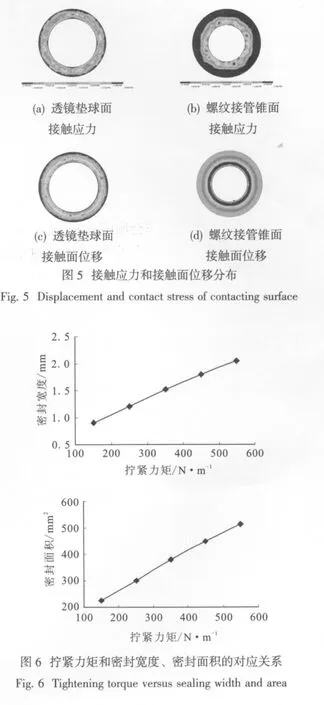
选取螺栓拧紧力矩分别为150，250，350，450和550五种工况进行了有限元计算，计算结果如表1所示。图5a和5b给出拧紧力矩为250 N·m作用下球面和锥面等效应力分布。从图中可以看出球面接触点区域的最大等效应力为295 MPa，锥面接触点区域的接触表面最大等效应力为144 MPa。接触面位移分布如图5c和5d所示。

根据计算结果得出拧紧力矩和密封宽度、密封面积的对应关系如图6所示。从这些图中可以看出，在螺栓拧紧的过程中，密封宽度和密封面积从零开始逐渐增大，当拧紧力矩达到550 N·m时，分别达到为2.058 mm及513.22 mm2。在拧紧力矩增大过程中，球头锥面的密封宽度和接触面积的增长速率在逐渐减缓，变化曲线趋于平缓。

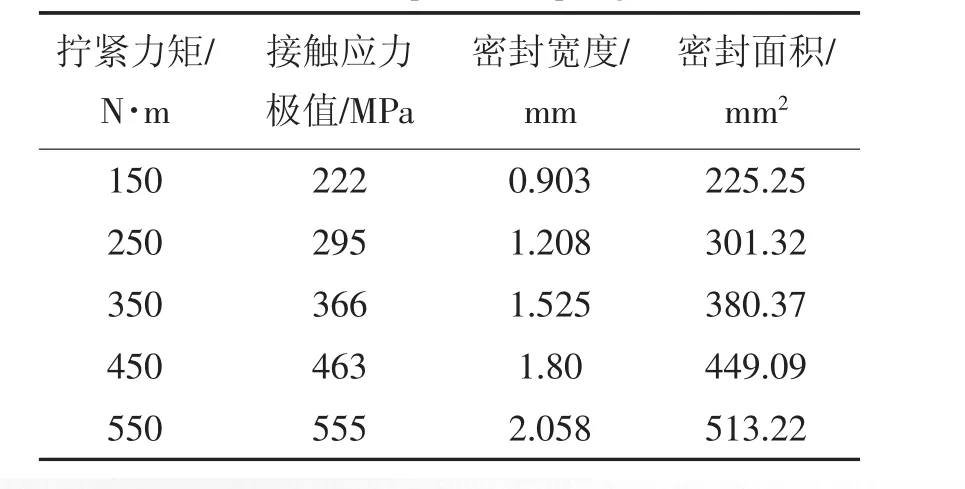
表1 透镜垫连接件有限元数值分析结果Tab.1 Results of finite element numerical analysis for lens spacer coupling

由于在密封结构设计方法中大都将接触应力作为密封性能的评价标准，接触面压力越大，密封联接越紧密，密封性能越好。从表可看出随着拧紧力矩的增大，平均接触应力也逐渐增大。在550 N·m力矩作用下，球面接触点部表面接触应力极值高达555 MPa，已高于透镜垫材料的极限强度，球面部分可能产生破坏。

2.5 压力试验

使用力矩扳手拧紧螺栓，拧紧力矩为250N·m进行了液压强度试验和气密试验。液压强度试验中，分为 25 MPa，35 MPa，49.5 MPa和 67.5 MPa四个压力级别进行，每级压力保压10 min，无渗漏；在67.5 MPa液压试验中，两法兰间有微量变形，但泄压后，变形回零。用45 MPa洁净干燥的氮气进行气密性试验，保压10 min未见漏气。

3 结论

以某高压组合件试车台增压系统管路连接结构作为研究对象，进行了密封计算和螺栓强度校核。采用有限元软件ANSYS对透镜垫结构进行数值模拟，考察了不同预紧力下的透镜垫结构等效应力分布和变形情况，得出了不同力矩和密封宽度、接触面积以及接触应力的对应关系。连接结构的液压强度试验和气密性试验表明在250 N·m拧紧力矩下，密封可靠，结构强度满足要求。

[1]郭霄峰主编.液体火箭发动机试验[M].北京:宇航出版社,1990.

[2]王勖成.有限单元法[M].北京:清华大学出版社,2003.

[3]陆培文.实用阀门设计手册[M].北京:机械工业出版社,2006.

[4]博嘉科技.有限元分析软件--ANSYS融会与贯通[M].北京:中国水利水电出版社,2002.

[5]尚晓江,邱峰,赵海峰,等.ANSYS结构有限元高级分析方法及范例应用 [M].北京:中国水利水电出版社,2006.

[6]任重.ANSYS实用分析教程 [M].北京:北京大学出版社,2003.

[7]许可,庞贺伟,孙刚.卫星推进系统管路装配技术研究[J].航天器环境工程.2006,23(6):363-368.

[8]李珊珊,韩丽俊,梁义维.基于ANSYS的斜齿轮接触应力有限元分析[J].机械工程与自动化.2009(4):23-24.

[9]陈署泉,肖曙红,杨士铁.角接触球轴承的静态接触分析[J].轴承.2009(11):4-7.

[10]温卫东,高德平.接触问题数值分析方法的研究现状与发展[J].南京航空航天大学学报,1994(5):664-670.

[11]刘涛,扬风鹏.精通ANSYS[M].北京:清华大学出版社,2002.

[12]郭乙木,陶伟明.线性与非线性有限元及其应用[M].北京:机械工业出版社,2003.

[13]张鑫,刘旺玉.基于ANSYS的永磁直流牵引电机接触有限元分析[J].机械设计与制造.2010(3):27-29.

[14]肖望强,段东平,李威,等.双压力角非对称齿轮轮齿接触分析[J].农业机械学报.2010,41(8):199-205.

[15]张妍,杜四宏,袁振伟,等.齿啮式快开门法兰的接触分析[J].压力容器.2010,27(3):26-29.