基于VB的巷道楔形体稳定性分析程序设计与实现＊

沈建波,郑文海,屈建国,詹召伟

(1.山东科技大学资源与环境工程学院, 山东青岛市 266510;2.济宁矿业集团落陵煤矿,山东邹城市 273516;3.济宁矿业集团运河煤矿, 山东济宁市 272100)

基于VB的巷道楔形体稳定性分析程序设计与实现＊

沈建波1,郑文海1,屈建国2,詹召伟3

(1.山东科技大学资源与环境工程学院, 山东青岛市 266510;2.济宁矿业集团落陵煤矿,山东邹城市 273516;3.济宁矿业集团运河煤矿, 山东济宁市 272100)

根据赤平投影的成图原理,应用 VisualBasic实现了楔形体稳定性分析的程序化。用户只需在VisualBasic界面上输入楔形体的相关参数,程序即可实现赤平投影的绘制、楔形体滑动方式的判断、稳定性系数的求解,使得楔形体稳定性分析更加方便和快捷。

赤平投影;VisualBasic;楔形体;稳定性分析

在巷道的围岩中,节理面有时会把围岩切割成楔形体,楔形体的稳定直接影响巷道的稳定,在这种情况下,分析和研究楔形体的稳定性是分析巷道围岩稳定性的关键。极射赤平投影图解法是分析楔形体稳定性的有效方法,根据赤平投影理论可以用Auto CAD完成作图,但是在实际的绘图中,不仅需要掌握赤平投影理论和楔形体稳定性判据,而且还要进行繁琐的绘图操作和稳定性判断,不但效率不高,而且容易出错[1]。本文应用 VisualBasic编制了赤平投影程序,利用 Visual Basic界面友好,操作方便,使用灵活的特点,用户只需输入楔形体的参数,由程序实现赤平投影的绘制和楔形体的稳定性判别,最终求出稳定性系数。

1 编程原理及理论分析

1.1 赤平投影原理

楔形体稳定性分析是在赤平投影上进行的。极射赤面投影是表示物体的几何要素或点、直线、平面的空间方向和它们之间的角距关系的一种平面投影[2]。它以 1个球体作为投影工具,过投影球球心的水平面称为赤平面,通过球心的直线与球面的交点称为极点,1条直线有 2个极点。铅直线交球面上、下 2个点 (也就是极射点)。将物体的几何要素置于球心,由球心射线将所有的点、线、面自球心开始投影于球面,就得到了点、直线、平面的球面投影[3]。再以投影球的上极射点或下极射点为发射点,将点、直线、平面投影 (点或线)投影于赤道平面上,这种投影就称为赤平极射投影,由此得到的点、直线、平面在赤平面上的投影图就称为赤平极射投影图。

1.2 楔形体稳定性判断

在巷道中,由节理面切割围岩形成的楔形体的稳定性判别可分 2个步骤,首先判断是否会滑动失稳,其次是判断滑动方式。

楔形体滑动是指楔形体在重力作用下,在楔形体内软弱节理面上产生的整体滑动。其滑动方向一般是由两节理面组合交线的倾向控制[4]。图1所示为巷道内一楔形体,面ABC为边墙临空面。假定只有摩擦力抵抗滑动,且 2个节理面的摩擦角相同,则楔形体可能滑动的条件是 2个节理面交线 (CD)的赤平投影 (点 I)应落在坡面大圆弧与摩擦圆所围成的范围内。

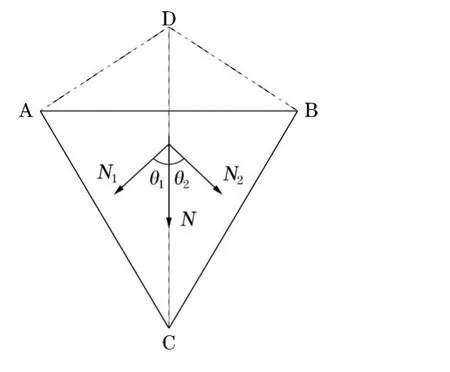
图1 楔形体

楔形体滑动方式有单面滑动和双面滑动 2种。当楔形体的几何形状一定时,楔形体各面的相对位置是固定的,楔形体是否滑动主要取决于楔形体在围岩中的空间位置状态,现以图2(a)中的楔形体为例,结合赤平投影图作以说明。假定交线 CD为基准线,巷道边墙 (即临空面)ABC保持产状不变,节理面ACD和节理面 BCD绕基准线 CD转动,在赤平投影图上巷道边墙与节理面 1的倾向夹角∠POM随之变动,当∠QOM大于∠QO I时,楔形体单面滑动,当∠QOM小于∠QO I时,楔形体双面滑动。

图2 楔形体赤平投影

1.3 楔形体稳定性系数的计算[5]

当楔形体节理面交线 CD的倾角为β,仅考虑自重W作用时,楔形体下滑力 F为Wsinβ。垂直交线CD的作用分量 N为Wcosβ。如图2,将 N分别分解到 2个滑动面,得到滑动面上的法向力 N1,N2为:

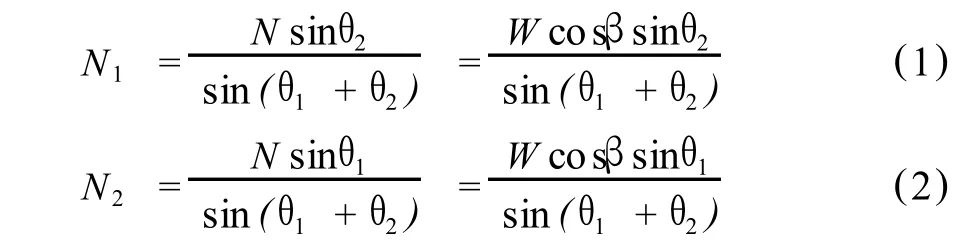
式中,θ1,θ2分别为 N与 2个滑动面法线间的夹角。

设滑动面ACD和 BCD的内聚力分别为 c1,c2,内摩擦角分别为φ1,φ2。则两滑动面的抗滑力之和为:

式中,S1,S2分别为滑动面 ACD和 BCD的面积。

则楔形体的稳定性系数为:

2 程序化实现过程

2.1 程序流程

程序流程图见图3,该程序流程可分为 2部分,第一部分判断滑动方式,首先输入楔形体的产状参数,根据输入的产状参数绘制出赤平投影,根据所绘的赤平投影作出滑动方式判断,滑动方式有单面滑动和双面滑动 2种,如果不滑动则结束程序。第二部分是稳定性系数计算,根据不同的滑动方式输入楔形体的力学参数,最终算出楔形体的稳定性系数。

2.2 编制程序

根据程序流程图,使用 Visual Basic 6.0编制程序代码和设计绘图界面 。Visual Basic是面向对象的可视化编程软件,具有程序设计简单和界面友好的特点。在程序设计和编制过程中充分利用这些特点,编制了程序代码并设计了绘图界面 (见图4、图5)。

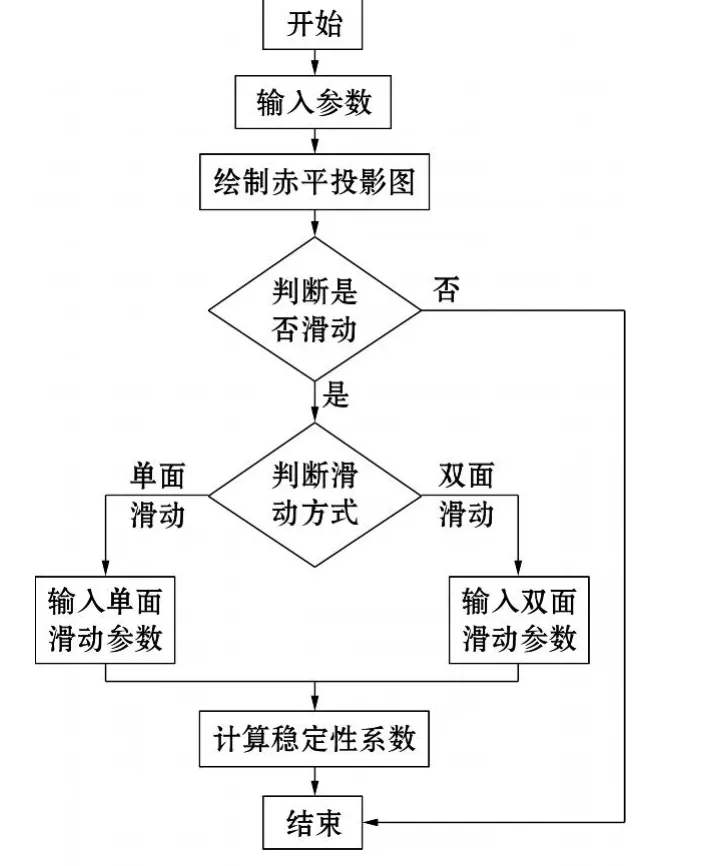
图3 程序流程

图4 程序界面一

3 程序的可行性评价及工程应用

3.1 程序的可行性评价

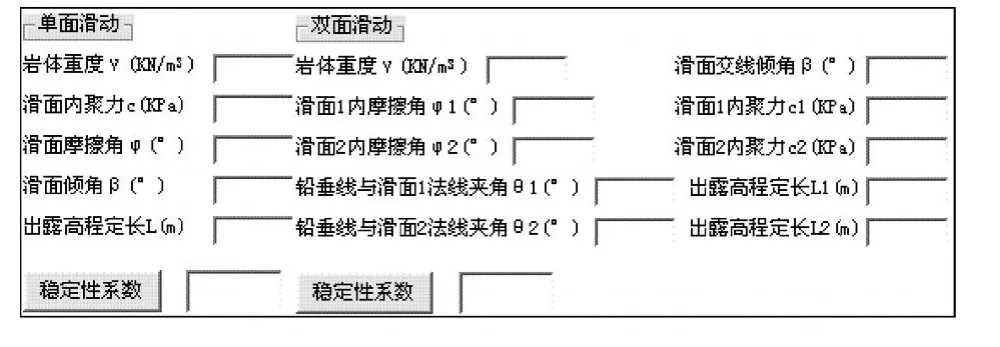
图5 程序界面二

某矿五采区一联络巷内,有一被节理面切割的楔形体,其参数如表1所示,经分析为一单面滑动楔形体,稳定系数为 1.43,现以此楔形体为例检验本程序的可行性。

表1 楔形体产状及其它参数

把表1中楔形体产状参数输入程序界面一,由程序绘出如图2(b)所示的赤平投影图,程序判断楔形体双面滑动,将楔形体的其他已知参数输入程序界面二,由程序计算出楔形体稳定性系数为 1.41,绝对误差仅 0.02,证明程序是可行的。

3.2 工程应用

矿井硐室的位置和轴线的正确设计是一项极其重要的工作。若选择的硐室轴线方向适当,则施工顺利,其围岩稳定性好,矿山压力小,支护简单,若选择不适当,则会给工程带来一系列的麻烦。一般情况下,要使巷道轴线方向尽可能垂直于区内的大型结构面,如大断层带、层间破碎带等,并与其结构面呈较大的夹角。这样,即使有较强的构造应力影响,其受力条件也最有利。

某矿一井下变电所为一长方形的大型硐室,围岩中有 3组主要的节理面:第 1组为小型冲断层,产状为 30°∠60°;第 2组为节理 ,产状为 255°∠70°;第 3组为发育的节理,产状为 350°∠60°。

运用本程序绘制赤平投影图,对井下硐室轴线方向作最优选择。首先由程序作出节理面的赤平投影图 (见图2(c)),其次在该图中选取硐室轴线方向,为了使硐室轴线方向能与 3组节理面均呈现较大角度相交,硐室轴线方向最好在节理面 (F2)和(F3)的走向方位之间选取。若选取硐室轴线方向为 35°,则它与各组结构面的交角分别是 86°、53°、52°,均为较大的锐角。同时 3组结构面与拱顶面、边墙面的夹角也较大 ,分别为 60°、70°、60°和 86°、44°、54°,对硐室围岩稳定都比较有利 ,当然 ,也还有局部不稳定的可能,南端墙以及由 3组结构面切割构成的楔形体,将在拱顶和南墙上构成可能不稳定体,这是不可完全避免的。将构成的楔形体,根据实际情况,测量产状参数,再结合其他参数,可运用本程序进行稳定性分析,此处不再赘述。

4 结 论

(1)对于巷道围岩中被节理面切割成楔形体的稳定性分析,应用极射赤平投影图解法分析是可行的。

(2)基于 Visual Basic的赤平投影程序能够实现楔形体的稳定性分析,使楔形体的稳定性分析变得方便快捷。

(3)应用赤平投影的经典理论,编制 Visual Basic程序,实现楔形体稳定性分析程序化的思想和方法,在工程实践中具有一定的使用价值和参考作用。

[1]陈永刚,等.赤平投影操作自动化初探[J].矿业研究与开发,2005,25(1):61-65.

[2]莫先恒,唐名富.赤平投影分析原理及在矿山地灾评估中的应用[J].中国水运,2007,10(7):150-151.

[3]赵文廷,卢 毅.极射赤平投影 CAD图解及其在岩质边坡稳定性分析中的应用[J].中国建材资讯,2007,34(6):42-48.

[4]高 全,等.楔形体及其稳定性分析与讨论 [J].路基工程,2008,(1):115-116.

[5]沈明荣,陈建峰.岩体力学[M].上海:同济大学,2006:198-199.

山东科技大学研究生创新基金资助项目(YCA090302).

2010-10-10)

沈建波 (1981-),男,山东邹城人,硕士研究生,从事矿山压力与岩层控制方面的研究。