高等教育发展与经济增长——基于我国四大区域面板数据的计量分析

周圆圆

(周口师范学院数学与信息科学系,河南周口466001)

高等教育发展与经济增长
——基于我国四大区域面板数据的计量分析

周圆圆

(周口师范学院数学与信息科学系,河南周口466001)

以新古典经济增长理论为基础,从高等教育与经济增长的内在关系出发,构建衡量高等教育发展与经济增长全貌的指标体系,并基于我国1978-2009年的相关数据,运用多元统计方法,对我国31个省级单位进行聚类分析,划分出四类区域,采用高等计量方法对两者之间的关系进行实证检验,在研究结论的基础上给出政策启示。

高等教育发展;经济增长;面板数据;单位根检验;协整检验

一、文献综述与问题提出

高等教育发展与经济增长的关系是教育经济学的基本理论问题。诺贝尔经济学奖获得者舒尔茨在美国经济学年会上宣读了《论人力资本投资》,被誉为教育经济学的独立宣言。随后,舒尔茨对人力资本理论进行了深化与系统化,全面分析了人力资本的含义与形成途径,揭示了人力资本和经济增长之间的关系[1-2]。

20世纪90年代以来,西方教育经济学研究在广度和深度方面均有突破。Greed在《高等教育经济学》一书中对高等教育的收费、税收、受教育者终身收入以及个人教育收益率等问题进行了深度探讨[3]。Mankiw和Barro等学者发现人力资本存量对经济增长有显著的影响,但两者长期的相关性不显著[4-5]。Sanders通过对美国50个州的高等教育与州国民收入关系的研究,发现不能得出高等教育支出促进了区域经济增长的稳健结论,而区域经济增长大大促进了高等教育支出的增加[6]。

国内学者刘贤龙对我国高等教育与经济增长关系进行了统计分析[7]。汤敏提出,若以每年增加25%～30%的速度,在3年内使中国高等学校的招生量增加1倍,可拉动近1 000亿元的投资与最终消费,对 GNP的贡献每年可达0.5个百分点以上[8]。崔玉平采用丹尼森和麦迪逊算法,计算了1982-1990年间我国高等教育对经济增长的贡献,并进行了国际比较,发现我国高等教育贡献率偏低,指出可以通过发展高等教育来提高教育对经济增长的贡献率[9]。胡永远、刘智勇运用面板数据模型,对中国1996-2001年高等教育对经济增长的贡献进行了计量分析,发现东部、中部、西部地区高等教育对GDP的贡献由高到低呈现梯次分布[10]。孙敬水、姚晶晶以内生增长理论为基础,对我国高等教育发展与经济增长的关系进行协整分析,发现两者之间存在长期均衡关系[11]。刘安利用菲德模型与面板数据求出1997-2005年间全国及各行政区高等教育对经济增长的贡献率,提出加大高等教育投入力度与合理调整投入结构的建议[12]。

目前,我国高等教育已实现从“精英教育”向“大众教育”的转变。在新的时代背景下,如何测度高等教育与经济增长之间的数量关系,协调区域高等教育发展与经济增长是一个重要的理论与现实问题。本文依据相关指标,运用多元统计方法,对我国31个省级单位进行聚类分析,划分出四类区域,形成了区域高等教育发展与经济增长研究的新视角。

二、模型选择、指标构建与数据来源

(一)模型选择

高等教育影响经济增长的理论模型都是以生产函数为基础,并结合外生经济增长模型和内生经济增长模型进行分析。本文主要基于Caselli经济增长模型[13],并结合我国高等教育发展的特点进行适当修改,得到高等教育对经济增长的影响模型。

模型的被解释变量是 GD PP,即人均 GDP;解释变量分别为 INV P、I、M、P、H与 W,其中 IN V P为人均社会固定资产投资,I为高等教育经费支出,M为高等教育规模,P与 H为高等教育质量因子,W代表高等教育存量水平。

(二)指标体系

依据模型(1),构建衡量高等教育发展与经济增长全貌的指标体系如下:

1.经济增长指标。用 GDP衡量经济增长是国际通行做法,本研究选用 GD PP代表人均国内生产总值,采用人均数,意在排除人口扩张对经济增长的影响。同很多研究采用增长率指标不同,本研究采用水平变量,其原因有:(1)符合经济增长理论的一般形式,如扩展的柯布—道格拉斯生产函数;(2)能够保留水平变量所包含的有用信息。

2.全社会固定资产投资指标。该指标可以代表衡量经济增长的物质资本因素进入计量模型,也可以作为衡量经济增长的辅助指标和独立的被解释变量进入协整方程,用于分析我国高等教育发展与整体投资规模效率之间的关系。由于我国经济波动与地方投资规模的扩张与收缩密切相关,我们引入该指标便于考察高等教育发展与经济稳定增长的关系以及对宏观经济波动的影响。IN V代表全社会固定资产投资总额,IN V P代表人均全社会固定资产投资总额。

3.高等教育投入水平指标。财政性教育经费的投入会影响到高等教育的发展水平、规模和质量,也间接刺激经济增长。因此,本文在实证研究中用高等教育经费支出来衡量高等教育的投入水平。考虑数据的可获得性,我们采用普通高等学校经费支出替代,用 I表示。

4.高等教育规模指标。高等教育规模的衡量指标众多,常见的有高等学校数量、招生人数、在校生人数、教职工人数等。在本研究中我们选择在校学生人数为衡量高等教育规模的指标,其中包括在校研究生人数、本科学生人数和专科学生人数,但不包括成人高等教育和民办高校在校生人数。计量模型中该指标用M表示。

5.高等教育质量指标。高等教育质量指标用高等学校师生比 P和高等学校人力资本水平 H代表。其中 P中的教师数量只指普通高等学校专任教师,不包括外聘教师和行政人员。而高等学校人力资本水平 H是指高等学校教师中高级职称人数。从理论和实际看,这种替代是可行的,一般来说高等学校专任教师的职称和数量反映了高等学校的人力资本水平。

6.高等教育存量水平。高等教育发展是一个系统,其发展过程中的各因素与发展积累结果都与经济增长之间存在联系。本文参照联合国教科文组织《统计年鉴》指标中的“每万人口拥有的大学生数”作为高等教育发展结果积累的指标,用W表示,其中大学生数包括专科以上学历。

本研究所有变量指标在计量分析时均采用对数形式(观测值取自然对数,变量名前加 L表示),原因有3个方面:(1)自然对数形式容易得到平稳时间序列,减少了对变量的差分次数;(2)异方差的存在将无法保证得到最佳的估计量,通过对指标进行对数调整,可以避免异方差性影响;(3)各变量均采用对数形式,可以在协整方程中直接得到各种作用弹性,便于考察解释变量的相对变化对被解释变量的影响。

(三)数据来源说明

统计数据来源:(1)国家统计局国民经济综合统计司:《新中国五十五年统计资料汇编》;(2)中华人民共和国教育部:《中国教育事业统计年鉴》各期;(3)中华人民共和国教育部:《中国教育经费统计年鉴》各期;(4)中华人民共和国国家统计局网站;(5)中华人民共和国教育部网站。

三、基于聚类分析的区域划分

聚类分析(Cluster Analysis)是研究分类问题的一种多元统计分析方法。采用原始指标,在SPSS16.0中选择层次聚类方法,对我国高等教育和经济发展状况进行聚类分析。我国高等教育发展聚类结果见表1,使用指标为 A1:高等学校在校生人数;A2:高校专任教师人数;A3:高校师生比;A4:高校高级职称人数;A5:每万人口大学生数;A6:普通高等学校经费支出额。我国经济发展水平聚类结果见表2,使用指标有 X1:人均国民生产总值;X2:人均全社会固定资产投资额①考虑文章篇幅的限制,相关指标数据作者可以通过电子邮件提供,作者电子邮箱:yuanyuanzhou1984@163.com。。

为了对我国区域高等教育发展与经济增长差异的关系进行科学地统计与计量分析,在高等教育发展与经济发展水平聚类分析结果的基础上,对我国31个省、直辖市和自治区进行重新划分。该区划包含四个层次:一类区域为高等教育及经济发展双发达地区,包含上海、北京、天津、江苏、广东、浙江;二类区域为高等教育发展水平较高,而经济发展水平发展中地区,主要有陕西、湖北、吉林、黑龙江、辽宁;三类区域为高等教育及经济发展水平双发展中地区,包括山东、福建、河南、河北、安徽、江西、山西、重庆、四川、新疆、内蒙古、广西、海南、甘肃、湖南;四类区域为高等教育及经济发展水平双落后地区,由西藏、宁夏、青海、云南、贵州组成。这四大类区域与我国官方划分的东、中、西三大地区有出入,是一种赋含教育与经济因素的划分方法。

表1 中国各地区高等教育发展水平聚类结果

表2 中国各地区经济发展水平聚类结果

四、基于四大区域面板数据的协整及因果关系分析

(一)面板数据单位根检验

在数据收集中发现,各地区高等教育经费投入数据很难获得。故在进行面板数据合成时,只保留衡量高等教育发展的 M、P、H与W指标,衡量经济增长的GD PP指标。对于人均全社会固定资产投资指标 IN V P,在实证分析时,将其看做一个控制变量,代表影响经济增长的资本因素。在面板数据协整及因果关系检验前,首先对经济增长(L GD PP)、投资(L INV P)、高等教育规模(L M)、高等教育质量(L P与L H)、高等教育存量(L W)6个变量分别进行ADF单位根检验,结果见表3。

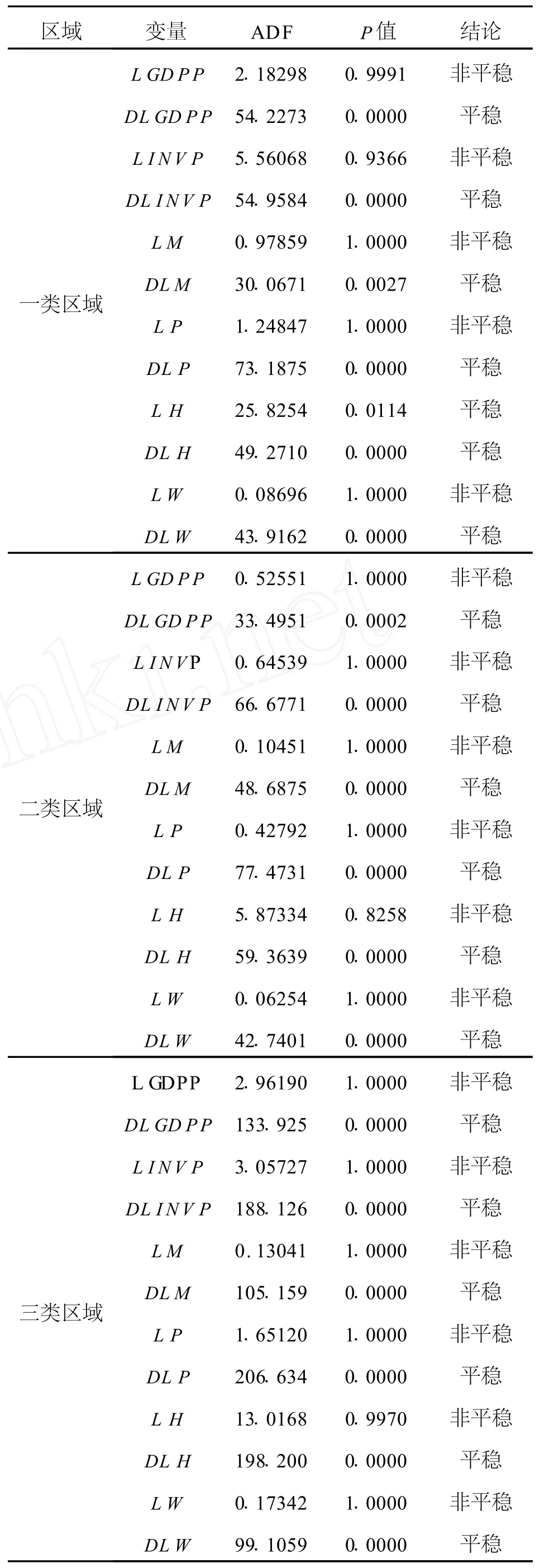
表3 面板数据单位根检验结果

表3(续) 面板数据单位根检验结果

结果表明,6个变量经过一阶差分后的序列均为一阶单整I(1)的,其中一类区域的L H不需要差分也是单整的,因此可以进行协整检验。

(二)面板数据协整分析

协整检验是考察变量间长期均衡关系的计量方法。协整思想是指若两个或多个非平稳的变量序列,其某种线性组合后的序列表现出平稳性,此时我们称这些变量序列间具有协整关系。因此协整检验前要求变量同阶单整。根据上节单位根检验的结果,满足此要求。协整检验方法主要有 Engle-Granger两步法和建立在向量自回归基础上的Johanso检验[13]。面板协整检验方法主要是将这两种方法推广到面板数据,比如 Pedroni和 Kao就是将Engle-Granger两步法推广到面板数据的协整检验上,Maddala和 Wu、Larsson et al对Johanson检验进行推广,建立出适合于面板协整的似然比统计量(LR)[14-16]。本文采用Pedroni的方法,以回归残差为基础构造出的7个统计量进行面板协整检验。在Pedroni检验中 Panel ADF和 Group ADF统计量较其他统计量有更好的小样本性质,因此在模型中主要参照Panel ADF和 Group ADF统计量来判断是否存在协整关系。结果见表4。

从表4的检验结果可以看出,在四类区域的L GD PP、L INV P、L M、L P、L H 与 L W 的协整检验中,Panel ADF和Group ADF统计量都通过了1%显著水平的检验,因此可以判断出,在四类区域中,变量 L GD PP、L INV P、L M、L P、L H 与L W 之间均存在长期稳定的协整关系。

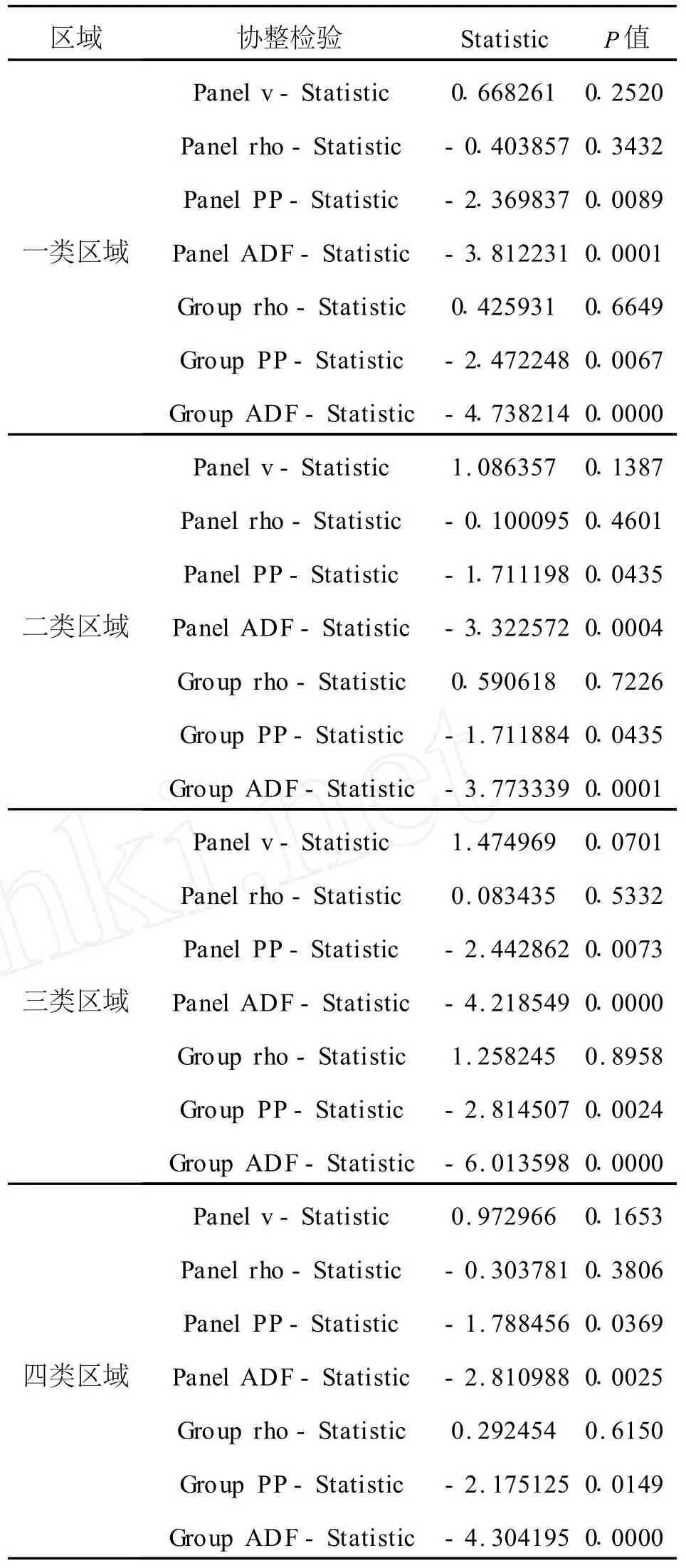
表4 面板数据协整检验结果

五、研究结论与政策启示

基于面板数据的协整检验表明:(1)在区域层面,Panel ADF和 Group ADF统计量都通过了1%显著水平的检验,表明我国高等教育发展与经济增长之间存在长期稳定的均衡关系。(2)在高等教育与经济双发达地区资本投入、高等教育质量以及高等教育存量对地区经济增长具有正向的影响,且资本投入影响最大,该区域经济增长主要依靠投资推动,该区域高等教育规模及高等学校人力资本水平不是经济增长的动因。(3)高等教育发达而经济发展中地区,其资本投入、高等学校师生比与高等学校人力资本水平对地区经济增长具有正向作用,而高等教育规模与高等教育存量对地区经济增长具有反向影响。(4)高等教育与经济双发展中地区,其资本投入、高等学校师生比及高等学校人力资本水平对经济增长起到促进作用,而高等教育规模与存量均对经济增长起到反向的影响。(5)高等教育与经济发展水平均比较落后的地区,其高等教育规模与高校师生比对经济增长呈反向影响,而其他因子均表现为正向促进作用,其中资本投入对经济增长促进作用最强,其他因子影响都不显著,该区域高等教育对经济增长的促进作用不明显。

通过对我国高等教育发展与经济增长关系的全面实证研究,可以得出以下政策启示:

(1)高等教育规模要与经济发展相适应。研究表明,以普通高等学校在校生人数为代表的高等教育规模与区域经济增长均呈负相关。从一定程度说明高等教育规模与经济发展不协调,特别是1999年高等学校扩招后,高等教育规模扩张过快。现阶段,我国高等教育规模不宜再扩大,应综合考虑区域经济发展水平、社会人才需求以及高等教育发展条件,逐步由追求高等教育数量增长转变为质量提高。

(2)优化人力资本配置,促进经济增长。协整及因果关系检验表明,反映社会人力资本积累水平的高等教育存量与经济增长呈现正向关系,且构成四大类区域经济增长的主要动力。通过加快工资制度改革与加强劳动力市场自由化建设,刺激个人对人力资本的需求,提高政府对人力资本的供给,形成高水平人力资本积累,促进经济快速增长。

(3)统筹高等教育与经济的协调发展。各级政府要加强对高度教育与经济发展的统筹规划,依据经济发展的中长期计划,预测未来社会经济发展所需的职业结构与人才数量,教育部门根据预测做好高等教育发展计划,确定各层次高等教育的规模与结构,避免高等教育资源浪费。

(4)实现区域高等教育均衡发展。实证研究表明:我国地区间高等教育发展与经济增长均存在显著差异,应根据各地区高等教育与经济发展的情况,制定与地方经济环境相协调的发展目标与策略,保持它们的持续健康发展。

[1]T W Schultz.The economic value of education[M].New York:Columbia University Press,1961:20-37.

[2]T W Schultz.Investment in human capital[J].The Economic View of American,1961(51):3-5.

[3]Greed J.The economics of higher education:an analysis of taxes versuses[J].England:Edward Elvar,1990:3-8.

[4]Mankiw G N.A contribution to the empirics of economic growth[J].Quarterly Journal of Economics,1997(107):407-437.

[5]Barro R J,Sala-I-Martin X.Economic growth[M].McGraw-Hill,1995:111-115.

[6]Sanders J.Does spending on higher education drive economic growth?20 Years of evidence reviewed[M].Goldwater Institue Policy Report,2003:2-15.

[7]刘贤龙.高等教育与经济关系的统计分析[J].统计与决策,1998(9):38-40.

[8]汤敏.教育启动消费呼之欲出[N].经济学消息报,1999-02-19(3).

[9]崔玉平.中国高等教育对经济增长率的贡献[J].北京师范大学学报:人文社会科学版,2000(1):31-38.

[10]胡永远,刘智勇.高等教育对经济增长贡献的地区差异研究[J].上海经济研究,2004(9):11-14.

[11]孙敬水,姚晶晶.高等教育发展与经济增长关系的协整分析[J].统计与决策,2008(2):75-78.

[12]刘安.谈高等教育对经济增长的贡献在高校扩招前后的变化[J].统计教育,2009(6):60-65.

[13]Francesco Caselli.Accounting for cross-country income differences[J].Handbook ofEconomicGrowth,2005(17):50-53.

[14]Pedroni P.Critical value for cointegration tests in heterogeneous panels with multiple regressors[J].Oxford Bulletin of Economics and Statistics,1999(61):653-678.

[15]Kao C.Spurious regression and residual-based tests for cointetration in panel data[J].Journal of Econometrics,1999(90):1-44.

[16]Maddala G S,Wu Shaowen.Acomparative study of unit root tests with panel data and a new simple test[J].Oxford Bulletin of Economics and Statistics,1999(61):631-652.

F224.9

A

1671-9476(2011)01-0121-05

2010-10-26;

2010-11-13

周口师范学院青年科研基金“基于MATLAB的空间计量经济建模及应用”(zknuqn200904)。

周圆圆(1984-),女,湖北黄梅人,讲师,硕士,研究方向为计量经济建模及应用。