基于CUDA的机载MIMO雷达杂波建模
王占广 罗忠涛 李 军 孙 颖
(电子科技大学 成都 611731)
1 引言
MIMO雷达作为一种新的雷达体制,近年来受到了国内外的广泛关注[1]。MIMO雷达发射正交或部分相关信号,形成宽波束,在抗信号截获、检测弱目标能力以及速度分辨力等性能上更有优势[2],但同时使MIMO雷达的运算数据量成倍增加。在下视探测目标时,机载雷达的回波复杂[3],文献[4]中机载雷达杂波模型具有通用性和实用价值。借鉴该模型,我们建立机载MIMO雷达的杂波模型。由于MIMO雷达系统和机载杂波的固有特性,该模型的运算量庞大不可避免,对平台硬件要求高,需要运行较长时间。
图形处理器(Graphic Processing Unit,GPU)以其先进的多核结构和强大的浮点计算能力为并行通用计算提供了很具发展前景的新型运算平台[5]。与CPU相比,GPU用于通用计算的性能高,成本低,内存和带宽资源大。CUDA(Compute Unified Device Architecture)是NVIDIA公司推出的通用并行计算架构,使GPU能够解决复杂的计算问题[7]。
MIMO杂波模型的算法在运算法则上的一致性和并行性,很好的符合了GPU并行运算的架构特性。针对CUDA编程模型的特点,对机载MIMO雷达杂波模型进行改进,引入更多的并行算法和线程,有效利用GPU资源,以提高计算效率。最后测试了模型结构和数据规模对GPU的加速效果的影响,以实现基于CUDA的并行运算的最优化,为MIMO领域广泛存在的大数据量运算提供了一条新的解决思路。
2 机载MIMO雷达杂波建模
2.1 杂波建模
机载MIMO雷达的杂波模型如图1所示。发射阵元数为NT,接收阵元数为NR,每个阵元均为全向天线,φ为地面散射体或目标的俯仰角,θ是地面散射体或目标的方位角。发射阵列和接收阵列为平行的均匀线阵,且二者距离较近。载机平台以速度υ沿线阵轴向运动。这样的假设符合大多数机载地面动目标显示系统。

图1 机载MIMO雷达杂波模型
图1第nT个发射阵元发射的窄带信号为sn(t)。每个相干脉冲处理间隔(CPI)发射K个脉冲,脉冲重复周期为Ts,积累时间TCPI=Ts×K。在地表面(海面)建立一个Δθ×ΔR的栅格单元,Δθ和ΔR分别为角分辨值和距离分辨值。从文献[3]可得:

其中λ为波长,B为NT个发射信号的总带宽。
第nT个阵元的发射信号到达第m个距离环第l个方位角杂波单元产生的回波,被第nR个阵元接收到的信号:
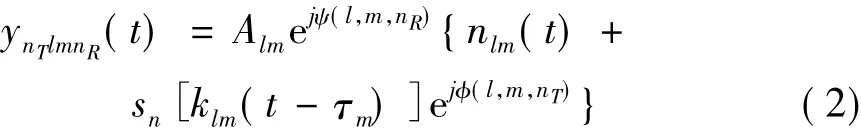
其中Alm为该杂波单元的反射系数,klm为多普勒效应压缩系数,τm为该距离环引起的时延,Alm为该杂波单元的反射系数,nlm(t)为噪声。φ(l,m,nT)为第nT个发射阵元引入的相位。ψ(l,m,nR)是第nR个接收阵元引入的相位。
第nR个接收阵元接收到的总回波为:

MIMO雷达的所有接收数据为NR个接收阵元的总回波构成的矩阵。
在该模型中,(2)式需要重复NT×M×L×NR次。为减少运算量,可以改进模型算法的计算顺序。方法主要有:a.尽量提取公因式,减少乘运算;b.尽量减少sn(t)的运算次数。因为在实验中发现,以文献[6]中的线性调频信号作为仿真信号,sn(t)算式复杂,是运算量大的一大原因。
改进后的算法为:先计算第m个距离环上第l个方位角杂波单元上对所有发射信号的总回波到达雷达接收阵元nR时的信号:
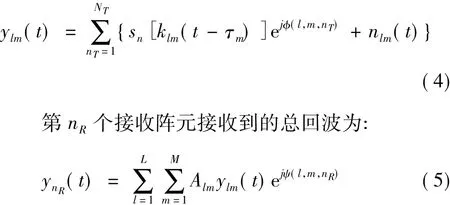
改进后的算法,其运行时间依旧不能令人满意(可参见4.1节中的仿真实例)。然而,改进计算顺序来减少运算量的空间已经不大了。
2.2 分析运算量
当机载雷达下视探测目标,地海杂波不仅强度大,多普勒频谱宽,而且可能在所有的距离上成为目标检测的背景[3]。这导致建模过程中需要模拟的物理量多,计算复杂;距离和角度范围大,需要建模的杂波单元多。
机载MIMO雷达的杂波模型运算量大,除了上面所说的机载雷达平台因素外,MIMO雷达系统特性的两个因素使它的运算量在相控阵雷达同类模型的运算量上成倍增加。
第一,由于MIMO雷达发射低增益的宽波束,因此需要长时间积累,通常TCPI是相控阵的M倍,导致建模时数据规模增为相控阵的M倍。
第二,相控阵雷达发射相干信号,MIMO雷达发射正交或部分相干信号,导致MIMO建模不能将发射波束合成来减小运算量。即MIMO雷达的sn(t)需要分别算,而相控阵可只计算一个sn(t)。
机载MIMO雷达的杂波模型在运算量上成倍增加,不仅延长了运算时间,而且其运算过程中产生和存储的数据同时也成倍增加,对硬件的要求也更高。一个雷达参数的典型设置,如4.1节中的仿真实例,足以使运行时间达到数小时。并且,数据存储达到数十万甚至百万,普通的仿真平台甚至不能满足。机载MIMO雷达杂波模型的大运算量,引起仿真历时长,影响科研进度;数据量过大,对硬件设备要求高。为解决此问题,有必要寻求适合的新方法和工具。
3 基于CUDA的建模
3.1 CUDA 架构
近年来GPU迅猛发展,在浮点数的计算能力和内存带宽上已经远远地超过了CPU。NVIDIA推出的统一计算设备架构CUDA,GPU推向通用计算的领域中[8]。
GPU的中心思想在于通过大量功能简单的流处理器共同运转来提高计算和数据的整体吞吐率。从硬件架构看,GPU包含有若干个线程处理群(Thread Processing Cluster,TPC),每个 TPC 包含数个流多处理器(Stream Multiprocessor,SM),每个SM中包含几个(一般是8个)流处理器(Stream Processor,SP)。SP即通常所说的 GPU的“核”。SP是GPU的基本执行单元,有自己的寄存器,但SM才具有取指、解码、分发逻辑的功能。隶属于同一SM的SP共用同一套取指和发指单元,也共用一块共享存储器。采用这样的硬件结构,使得GPU优于执行并行计算。
与硬件架构相对应的是,在编程模型上CUDA采用了SIMT(Single Instruction,Multiple Tread,单指令多线程)执行模型。CUDA编程模型将CPU作为主机,GPU作为协处理器或者设备。运行在GPU上的CUDA并行计算函数成为内核函数(kernel),内核函数一般由超多线程执行,由主机端调用。内核函数通过将数据抽象到线程层次中,可以使用GPU的SIMT多处理器对数据进行并行的计算。
CUDA通过三层层次结构来管理并行线程。最基本的线程(thread)组成线程块(block),一定数量的线程块组织成线程网络(grid)。同一个block内的线程可以相互协作,通过共享存储器来共享数据,实现对加速程序的精细操作。同一个block的线程会在同一个流多处理器中执行,而一个流处理器可以同时有多个block。block中线程数量的大小有限度,合理分配block的大小,使流处理器对thread并行运算多次,这样隐藏了thread与thread之间和block与block之间读取和存入延迟,更好地利用执行单元的资源,提高并行运算的效率。
3.2 基于CUDA的建模算法
本文第2部分分析出机载MIMO雷达杂波模型的计算公式。再研究该算法,不考虑物理意义,仅从数学角度分析杂波模型的数学算式。可以发现,模型算式看似十分复杂,实则 smnlRlθ(t)作为 nT、l、m、nR、t五个参数的初等函数,运算法则是一致的。并且,其中大量运算是加减乘除和指数运算,并没有分段、判断或迭代等逻辑性强的运算。该模型的运算量大,是源于同一运算法则的巨量次反复计算。运算法则的一致性和并行性,有利于CUDA架构发挥其在大规模并行运算上的特性。
根据GPU的架构特性和CUDA的编程特点,对模型的原算法进行适当的改变,使新算法有尽量多的并行算式,编程时执行尽量多的并行线程。具体思想是:在时间t序列上,某个杂波单元对某个发射信号的回波数据可以对应于thread的ID号并行运算来产生;杂波单元不同,以及发射阵元和接收阵元引入的变化(比如 τm、Alm、klm等),可看做因 nT、l、m、nR变化的参数;如此一来,数据的运算法则一样,不一样的是参数,适合改编于kernel函数中。同个时间序列上的点,在同个block中实现并行运算;同一个杂波单元对同一个发射通道的计算法则是一样的,归于同一个grid;接收阵元或杂波单元不同,采用kernel外的循环计算。总之,在CUDA编程结构的三个层次上,实现运算法则相同,导入参数不同,如此生成各接收通道数据。
图2给出了机载MIMO雷达杂波模型的CUDA实现流程图,大体上有以下四步:
第一,设置雷达、杂波和目标等参数,通过CUDA函数传入显存,进入 kernel函数,开始 GPU运算。
第二,进行线程规划,依据杂波模型中阵元个数和杂波单元数。
第三,计算杂波单元的回波信号。并行线程的参数,存储在共享存储器中,提高运算速度。
第四,计算各通道的接收信号,并将结果从显存导入内存,退出kernel函数,结束GPU运算。

图2 基于CUDA的机载MIMO雷达杂波模型的编程流程
4 实验测试
4.1 仿真实验
为测试机载MIMO雷达杂波模型的GPU运算效果,分别对基于CPU和CUDA的建模进行仿真。
仿真平台:处理器 CPU为 Intel i5750,物理4核,主频2.66GHz,内存4G,GPU 为 GTX465,单精度浮点计算能力897GFlops。Windows XP系统,编程环境:visual 2005,CUDA编译器nvcc2.0。
雷达参数:设定一个MIMO雷达的典型值。载机高度 H=8km,υ=120m/s,发射阵元数 NT=8,接收阵元数NR=16。发射信号为线性调频信号,带宽B=0.2MHz,λ =0.246m,脉冲发射周期 Ts=0.5ms,K=32,TCPI=0.016s,采样频率 f=3.2MHz。
依据2.1节中的建模,取Δθ=0.1,ΔR=100m。研究在角度范围π,距离0-80km的杂波模型,杂波单元有25600个,时间序列长度NCPI=51200。最终产生NR个接收阵元的接收数据,排列为16×51200的矩阵。在此设置下,数据规模达到了80多万,CPU需要运行近4h,GPU只需要运行近4min,加速效果非常明显。
4.2 CUDA运算的验证
为验证CUDA运算的正确性,对模型中的接收数据进行杂波谱分析,结果如图3,与CPU运算结果一致,说明基于CUDA的机载MIMO杂波模型是正确的。
4.3 效率测试
上一节的仿真实验证明了CUDA加速建模的可行性,在这一节,测试雷达参数不同对加速效果的影响,并分析如何建模能更好发挥GPU的并行计算能力。
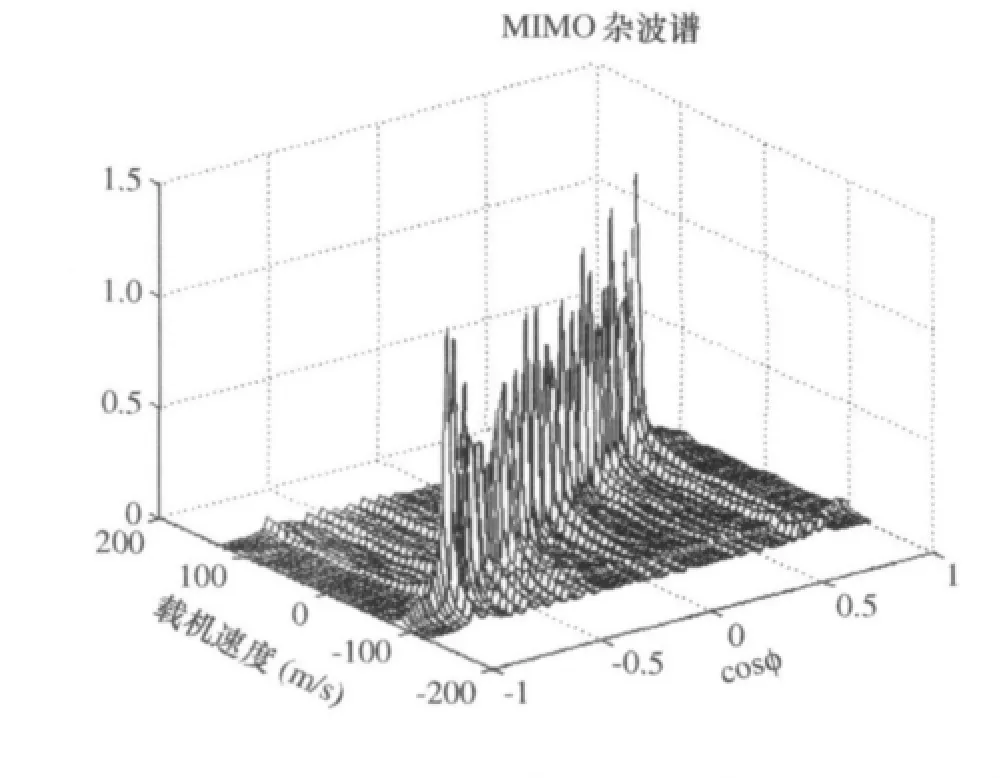
图3 基于CUDA的机载MIMO雷达杂波谱
在MIMO雷达系统的参数中,常修改的参数主要有发射阵元数,接收阵元数,脉冲积累时间,杂波距离环和测角度范围等。根据3.2中杂波建模思想,从中挑选积累脉冲数K和接收阵元数NR作为测试参数,因为一方面二者影响着数据规模NR×NCPI,另一方面,同样的数据规模下,不同的(K,NR)代表不同的模型结构。各(K,NR)设置下GPU和CPU的运算对比如表1所示。

表1 机载MIMO杂波建模在CPU与GPU运行时间对比(单位:s)
数据规模越大,CUDA加速效果越明显。这在NR=16时的测试中可以明显地看到。当数据规模增加一倍,CPU运行时间也几乎增加一倍,CUDA运行时间则更少。CUDA的加速比在数据规模小时并不明显,其意义主要在于大规模数据运算。当数据量过大,CPU内存已经无法正确运行出结果时,GPU硬件资源依然能够支持程序运行。
再看模型结构。相同的数据规模,CUDA运算时间差异很大,如(K,NR)=(4,64)或(16,16)。加速比随着K增大而急剧增加,随NR增大而缓慢增加,这要归结于模型结构的因素。如前所述,同一个时间序列上的数据,通过一个kernel函数并行运算,故K能直接影响CUDA并行运算的速度;不同接收通道的数据,是在外部循环调用kernel函数,故NR对加速比影响不大。这说明模型结构与加速效果影响甚大。因此,在设计基于CUDA的算法和编程中,应当尽量避免kernel内外的判断循环等逻辑,使kernel中含有最多的并行同个运算,利于CUDA加速运算。
此外,GPU加速比除了与编程结构和数据规模有关,也与GPU和CPU本身硬件上的运算能力有关。一般来说,比起同规格的CPU,GPU无论在浮点计算能力、内存和带宽上都占有优势。只要正确地设计算法和编程,将GPU的并行运算潜力挖掘出来,它的计算能力能达到CPU的数十倍。
5 结束语
本文主要研究了基于CUDA的机载MIMO雷达杂波模型的实现,测试了模型结构和数据规模对加速效果的影响,。仿真实验表明,本文提出的基于CUDA建模,发挥出了GPU在并行通用计算的长处,相比传统CPU,CUDA运算准确,速度提升数十倍,并能胜任更大规模的运算量。
机载MIMO雷达属于发射分集的MIMO雷达。对于其他系统的MIMO雷达,以及MIMO雷达中并行计算量丰富的其他阶段,结论同样适用。为使GPU能够在更广阔的领域发挥威力,未来的研究将专注于进一步提高计算效率,以及将CUDA应用于更深入的阶段,比如在信号处理时,匹配滤波和傅里叶变换涉及的运算量更加庞大。
[1]E Fishler,A Haimovich,R Blum,et al.MIMO radar:An idea whose time has come[C].Proc.of the IEEE Int.Conf.on Radar.Philadelphia,PA,April 2004.
[2]何子述,韩春林,刘波.MIMO雷达概念及其技术特点分析[J].电子学报,2005,33(12A):2441-2445.
[3]贲德,韦传安,林幼权.机载雷达技术[M].北京:电子工业出版社,2006.
[4]R Klemn.Adaptive clutter suppression for airborne phased arrays.IEE Pro.F.1983,130(1).
[5]MACEDONIA M.The GPU enters computing's main stream[J].IEEE Computers,2003.
[6]刘波.MIMO雷达正交波形设计及信号处理研究[D].四川:电子科技大学电子工程学院,2008.
[7]NVIDIA.NVIDIA CUDA Programming Guide Version 2.1[Z].2008.
[8]张舒,褚艳利,赵开勇.GPU高性能运算之CUDA[M].北京:中国水利水电出版社,2009.

