含空洞的马步型哈密顿圈探索

杨克昌,刘志辉

(1.湖南理工学院 计算机学院,湖南 岳阳 414006;2.湖南电视台,长沙 410000)

含空洞的马步型哈密顿圈探索

杨克昌1,刘志辉2

(1.湖南理工学院 计算机学院,湖南 岳阳 414006;2.湖南电视台,长沙 410000)

通过搜索某些特殊的较小马步遍历,将其按照一元旋转与二元支撑两种组合模型构建成含空洞的马步型哈密顿圈,拓广了哈密顿圈图论课题的研究范围.

马步哈密顿圈;空洞;组合;递归;回溯

引言——马步遍历与哈密顿圈

马步遍历与马步型哈密顿圈是一个集趣味性与学术性于一身的组合图论问题.

在给定的方格棋盘中,马从棋盘的某一格出发,按马走“日”的规则经过棋盘中的每一个方格恰一次,该问题称为马步遍历问题,经过棋盘的每一个方格恰一次的线路称为马步遍历路径.

马步遍历中若终点能与始点相衔接,即遍历路径的终点与始点也能形成一个“日”形关系,该遍历路径为一马步封闭圈,称为骑士巡游圈,或称马步型哈密顿圈,以下简称哈密顿圈.

本文探讨含空洞的哈密顿圈,即探索在方格棋盘中含有一个马步不能踏入的空洞区域的哈密顿圈.这显然是一个比寻求一般意义上的马步遍历或哈密顿圈更具挑战性的课题.

如果棋盘中的空洞只是某一单个空格,只需在搜索哈密顿圈的程序中加入“障碍空格”的条件限制即可.当棋盘中的空洞为一片空格区域时,因为此时棋盘参数必然比较大,同时空洞限制比较复杂,应用常规回溯或递归设计来探索很难切入.本文给出两个组合模型实施构建,即通过搜索棋盘参数较小的始点与终点满足某些特殊要求的马步遍历,用这些遍历按给定的组合模型构建成含空洞的哈密顿圈.

1 一元旋转模型构建

一元旋转组合模型,即只一个特殊的马步遍历通过旋转组合成含空洞的哈密顿圈.

1.1 一元旋转组合模型

设一元旋转组合模型的组合元素为n行m列的遍历A,按如图1所示的旋转模式实施组合:遍历A作为基础横放在棋盘下部,棋盘左边模块为组合元素A逆时针旋转270°后列倒置而成,右边的模块为组合元素A逆时针旋转90°后列倒置而成,横放棋盘上部的为A遍历旋转180°所得.

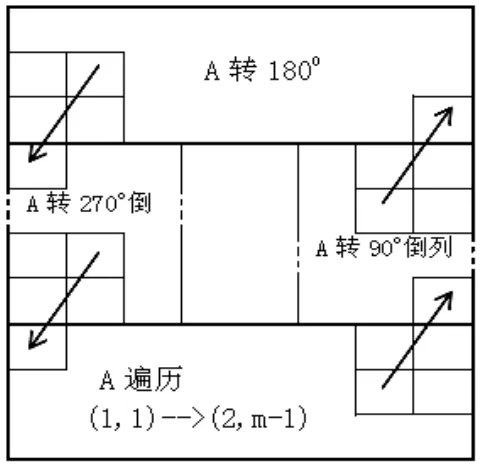
图1 一元旋转组合模式

按如图1所示的一元旋转组合模式,遍历A的始点与终点定为(1,1)与(2,m−1),注意到终点(2,m−1)既可与下一个同向遍历的始点(1,1)相衔接,也可以与逆时针旋转 90°后列倒置遍历始点(1,1)相衔接,因而组合可以进行横竖两个方向的任意扩展.

设棋盘的上下部各设置wh个遍历,左右部各设置wv个遍历,则所得含空洞的哈密顿圈共走2(wv+wh)mn步,棋盘为 (2n+wvm)×whm,中央所含空洞为wvm× (whm-2n).

注意到whm≤2n时组合时无空洞,而当n＜ 3时无遍历,显然要求whm＞ 2n≥6.

1.2 探索遍历回溯设计

应用回溯设计探索在nm广义棋盘中指定始点为(1,1)、终点为(2,m−1)的马步遍历.

设置数组x(i),y(i)记录遍历中第i步的行列位置,二维数组d(u,v)记录棋盘中位置 (u,v)即第u行第v列所在格的步数值.

例如第 9步走在棋盘的(3,2)格,则x(9)= 3,y(9)= 2;d(3,2)= 9.若d(i,j)= 0,表示棋盘中的 (i,j)格为空,可以走位.

注意到马走“日”形最多可走8个方向,图2所示当马处在(x,y)时可选的8个方向.

图2 马步可走的8个位置

设置控制马步规则的数组a(k)、b(k),若马的当前位置为(x,y),马步可跳的8个位置为(x+a(k),y+b(k)),k= 1,2,… ,8.其中

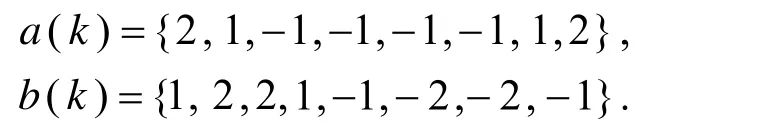
在回溯过程中,需知第i步到第i+ 1步原已选取到哪一个方向,设置t(i)记录第i步到第i+1步已选取的方向数,回溯时只要从t(i)+1～8选取方向即可.

回溯从i= 1开始进入条件循环,条件循环的条件为i＞0.当i＞0时还未完成回溯,可试探走马.

设置k(t(i)+1～8)循环依次选取方向,并求出此方向的走马位置:u=x(i)+a(k),v=y(i)+b(k).

判断:若1 ≤u≤n, 1≤v≤m,d(u,v)= 0,即所选位置在棋盘中且该位为空,可走马步d(u,v)=i+ 1;同时记录下此时的方向t(i)=k,q=1标志此步走马成功,退出选方向循环.

第i步走马成功后,检测若i=mn- 1,且满足终点条件(u= 2,v=m- 1),标志已搜索到满足组合要求的遍历A,即进入组建并输出含空洞的哈密顿圈.

第i步走马成功后,检测若i=mn- 1,还未完成遍历,经i=i+1继续下一步探索.

第i步选取8个方向若保持q=0,即i时的8 个方向均不能走马,在此卡住,不能再向前了,于是方向t(i)与此时马位清“0”后,经i=i-1迭代回溯到前一步继续探索.

当回溯到i=0时,所有结点搜索完成,结束.

1.3 棋盘左上角置“1”规范化输出

哈密顿圈是一个封闭圈,无所谓起点与终点.为方便查阅,习惯把棋盘的左上角置“1”进行规范化输出.

棋盘左上角遍历按遍历A旋转180°实际输出,注意到此时棋盘左上角元素实为 A遍历的d(n,m).因而可设e=d(n,m)- 1,组合圈的每一步均减去e,这样使棋盘左上角置“1”.

同时,为衔接必需,根据图1所示逆时针构建中各遍历所在位置进行调整:

左边从上至下共wv个遍历的元素需分别加上mn、…、wvmn;

下部从左至右横排的wh个 A同向遍历的元素需分别加上(wv+1)mn,…,(wv+wh)mn;

右边从下至上共wv个遍历的元素需分别加上(wh+wv+ 1)mn, … ,(wh+2wv)mn;

上部从右至左横排的wh-1个同向旋转遍历元素需分别加上(wh+ 2wv+ 1)mn, … , (2wh+ 2wv-1)mn;

最后,棋盘左上角遍历中出现的所有非正项均需加上 (2wh+2wv)mn.

1.4 构建实例与说明

遍历为n行m列 (m＞2n),请输入n,m:3,8

选择wh=wv= 1,构建如图3所示,即得一个14行8列棋盘,中央含8行2列空洞的哈密顿圈.

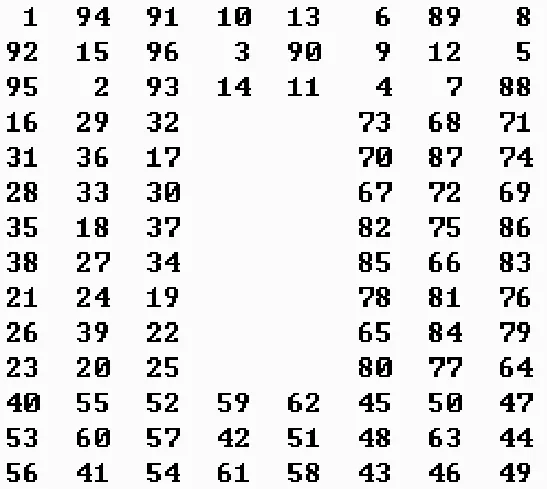
图3 96步含空洞的哈密顿圈

该含空洞的哈密顿圈共有96个马步！

应用一元旋转组合模型构建,遍历A还可选3×7、3×9、3×10等.

简单构建时选择wh=wv=1即可,若一般地扩展到横排wh个遍历、竖列wv个旋转遍历(这里wh与wv分别为从键盘输入的任意大于 1的正整数),此时要求whm＞ 2n≥ 6,而构建元素除以上列举参数外,遍历A还可选 5×5、5×6 等.

2 二元支撑模型构建

二元支撑组合模式,即需用两个不同的马步遍历A,B通过支撑组合构建含空洞的哈密顿圈,如图4所示.

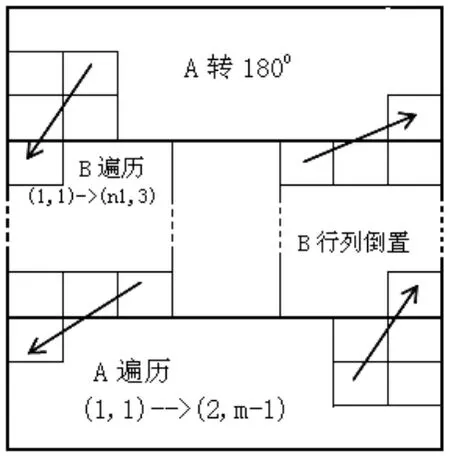
图4 二元支撑组合模式

2.1 二元支撑组合模型

二元支撑组合模式的组合元素遍历A同前,即为n行m列,始点为(1,1),终点为 (2,m-1);设组合元素遍历 B为n1行m1列,始点为(1,1),终点为(n1,3).

按如图4所示的二元支撑组合模式,遍历A终点(2,m-1)既可与下一个同向的A始点(1,1)相衔接,也可以与异向的 B始点(1,1)相衔接;而遍历B终点 (n1,3)既可与下一个同向的 B始点(1,1)相衔接,也可以与异向的 A始(1,1)相衔接,因而构建时可以进行横与竖两个方向的任意扩展.

设上下部设置wh个遍历A,左右部设置wv个遍历B,则所构建的含空洞的哈密顿圈共走2whmn+2wvmn步,构建的棋盘为 (2n+wvn1)×whm,所含空洞为wvn1× (whm-2m1).

注意到whm≤2m1时组合无空洞,显然要求whm＞2m1.

2.2 探索组合遍历递归算法设计

注意到构建需探索两个不同的遍历元素,拟采用递归设计实施探索.

建立递归函数:探索在n×m棋盘中始点为(x,y)、终点为(x1,y1)的马步遍历.

递归过程中,栈保留了递归过程中的各个状态的参数,因而可省略以上回溯设计中的t,x,y数组.控制马步规则的a、b数组与二维数组d(i,j)同前.

在控制k循环中若对所有k= 1,2,… ,8,候选位置(u,v)均不满足走马条件(或位置出界,或位置非空),则通过实施回溯,继续前一步的检测.

若第g步全部8个位置已走完,则回溯到g-1步.对于g-1步,k=k+1后继续检测,直到该步8个位置已走完时,又回溯到前一步.若第g步走步成功且g＜mn,则g+1后递归进入下一步探索.整个程序依此进行递归检测与回溯,直到回溯到第1步结束.

当走到第g步时,若mn且满足终点条件(u=x1且v=y1)时,即已搜索到指定遍历,标志量q=1,返回主程序.若 =mn但不满足终点条件时,则g=g- 1继续搜索.

主程序两次带不同的始点 (x,y)与终点 (x1,y1)调用递归函数搜索遍历B、A.首先若探索B成功,则把d数组元素赋值给c数组,同时d数组元素清0,为接着探索A遍历作准备.

若两次探索成功,则按左上角置“1”规范(同前,具体数据作相应修改)输出组建的含空洞哈密顿圈.两次调用若存在一次搜索不成功,输出“没有合适的遍历”而结束.

2.3 构建实例与说明

遍历B为n1行m1列,请输入n1,m1:4,3

遍历A为n行m列(m>2m1),请输入n,m:3,10

选择wh=wv= 1,得如图5所示棋盘为10行10列,中间空洞为4行4列的哈密顿圈.

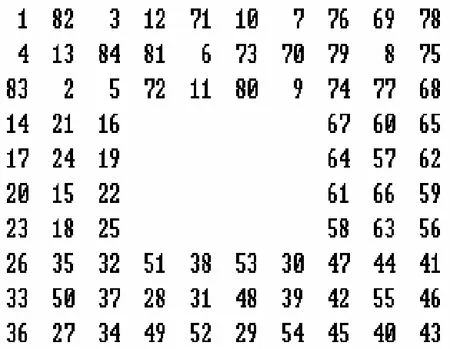
图5 84步含空洞的哈密顿圈

该含空洞的哈密顿圈共有84个马步.

由输出结果看,马步从棋盘左上角开始,围绕中央空洞潇洒走一“回”(“回”字通道宽度为 3格),最后又回到出发点.

应用二元支撑组合模型构建时,遍历A的参数同前列举,而遍历B可选3×9、3×11、4×3、4×5、5×5等.

3 结束语

应用组合模型对含空洞的哈密顿圈的探索与构建,拓广了哈密顿圈图论课题的研究范围.

以上提供的两个构建含空洞的哈密顿圈的组合模型也可以构建某些棋盘参数较大的不含空洞的哈密顿圈.

应用一元构建组合模型时,如果参量m=n(例如m=n= 5),选择上下部各设置2个A,左右各设置wv个A时可构建棋盘为(wv+ 2)n×2n的不含空洞的哈密顿圈.应用二元构建组合模型时,如果输入的参量满足m=2m1(例 如n1=4 ,m1=5,n= 3,m=10)时也有可能构建棋盘为(2n+n1)×m不含空洞的哈密顿圈.

应用常规回溯或递归搜索哈密顿圈,当棋盘参数较大时,因相应回溯层次太多或递归深度太深而显得无能为力,采用以上组合方式是一个较好的解决途径.

在给定棋盘的行与列,同时给定中央空洞的行与列的哈密顿圈搜索时,必须根据具体实际选择组合模型与运行参数.

本文推出的两个组合模型只限空洞在棋盘中处于上下对称、同时左右也对称的正中央,如果要求空洞在棋盘上下或左右有偏移时,必须设计更复杂的多元组合模型.

[1]宁安琪,宁宣熙.有洞棋盘的马步哈密顿圈问题及其实证研究[J].小型微型计算机系统,2004,(12):2126～2130

[2]宁安琪,宁宣熙.正方棋盘中广义马步哈密顿圈问题的若干研究结果[J].小型微型计算机系统,2005,(09):1551～1555

[3]徐尚进.有向图具有哈密顿圈的一个充要条件[J].广西大学学报(自然科学版),1999,(2)

[4]宁宣熙.堵塞流理论及其应用[M].北京:科学出版社,2005

[5]Zhu Yu-long,Shi Gang.Two new solutions for the Knight's tour problem[J].Mini-Micro Systems,1996,17(8):51～59.

[6]Ning Xuan-xi.Study on application of blocking flow theory in determination of Hamiltonian Guaph[R].Report on Aeronautical Science and Technology of China,GF-99045.(1999)

[7]Kevin McGown,Ananda Leininger.Knight's tour[EB/OL].http://oregonstate,edu/garityd/reu/.

Knight’s Circuit Tour on a Chessboard with Holes

YANG Ke-chang1,LIU Zhi-hui2
(1.College of Computer Science,Hunan Institute of Science and Technology,Yueyang 414006,China;2.Hunan Broadcasting System,Changsha 410000,China)

By searching some particular and small-scale knight’s path tours,this paper assembles them in accordance with two combination models into a knight’s circuit tour on a chessboard with holes,thus the scope of the study on Hamiltonian graphs theory is extended.

Knight’s circuit tour;hole;combination;recursion;backtracking

TP311.1;O157

A

1672-5298(2011)01-0012-05

2010-12-21

杨克昌(1946− ),男,湖南冷水江人,湖南理工学院计算机学院教授.主要研究方向:组合数学与算法设计