单晶铜纳米线的形变行为对温度和速率的依赖关系
朱铁民 侯 进*, 王奋英 高亚军 赵健伟*,,2
(1南京大学化学化工学院,生命分析化学教育部重点实验室,南京 210008)(2西南交通大学,信息科学与技术学院,成都 610031)(3南京大学计算机软件新技术国家重点实验室,南京 210093)
单晶铜纳米线的形变行为对温度和速率的依赖关系
朱铁民2,3侯 进*,2,3王奋英1高亚军1赵健伟*,1,2
(1南京大学化学化工学院,生命分析化学教育部重点实验室,南京 210008)(2西南交通大学,信息科学与技术学院,成都 610031)(3南京大学计算机软件新技术国家重点实验室,南京 210093)
本文采用分子动力学模拟的方法,分别考察了应变速率为0.02%·ps-1,0.2%·ps-1和2%·ps-1,温度为100,300和600 K下的[100]单晶铜纳米线的单轴拉伸形变行为。通过纳米线在形变过程中的原子排布,机械性质,径向分布函数和能量曲线分析,可得出纳米线的低速,中速,快速拉伸形变分别对应于原子的平衡态,准平衡态和非平衡态运动;纳米线的低温,常温,高温拉伸形变分别对应于原子的结晶态,局域无序和非晶态的运动。
分子动力学;纳米线;结晶态;局域无序
近年来,金属纳米线以其好的光、电、磁和机械性能,受到了人们的广泛关注。在微纳器件制备中,纳米线在机械拉伸过程中的形变行为直接影响了纳米线应用的可靠性。因此,研究纳米线的拉伸形变不仅对微纳米器件的应用开发具有重要作用,同时也在材料力学,纳米化学等基础学科领域具有重要意义[1-3]。
金属纳米线由于表面原子数所占比例高,其拉伸过程所表现的行为与块体材料不同[1-5]。表面原子具有低配位数[6],有别于体相原子,因此在拉伸过程表现出特殊的性质。迄今由于原子在微观世界的全同性,实验中难以将表面原子和体相原子加以区别。纳米线的机械形变尚存在一系列的基本问题。例如,表面原子是否在应变过程中被体相原子取代,纳米线在拉伸过程中颈缩是由表面原子还是体相原子参与,纳米线断裂前所形成的原子线是由表面原子还是体相原子构成等[7-8]。
实验手段难以回答上述问题,但分子动力学模拟可以从一个侧面给出拉伸过程中原子排布的细节[8-11],本文将利用分子动力学方法,将物理化学性质上全同的原子划分为表面原子和体相原子。重点考察低配位的表面原子在形变过程中的作用。
1 实验部分
本文采用经典分子动力学模拟的方法研究了8a×8a×12a(a为铜的晶格常数)的[100]单晶铜纳米线在拉伸过程中的形变行为。首先,纳米线自由弛豫(包括固定层),弛豫允许其纳米线自由收缩,当原子的平均势能达到一个稳定值,并且原子所受的平均应力在0.0 GPa轻微波动时,即可认为纳米线达到稳定状态。然后,纳米线两端的固定层原子沿z轴匀速运动,考察了体系在不同应变速率和温度下的拉伸形变行为。应变定义为ε=(l-l0)/l0,其中l是形变后的纳米线长度,l0是其初始长度。应变速率分别为0.02%·ps-1,0.2%·ps-1和 2%·ps-1; 模拟温度分别为100,300 和 600 K。 在拉伸阶段采用 Nosé-Hoover的方法进行速率标定[12-14],使体系处于恒温状态,蛙跳法做路径时间积分[15],模拟步长为1.6 fs,采取自由边界条件。
利用嵌入原子势(embedded atom method,EAM)来描述铜原子间的相互作用[16-18],该势函数中,每个原子的势能包括与其他原子作用能和电子云形成的嵌入能两部分,具体表示如下:
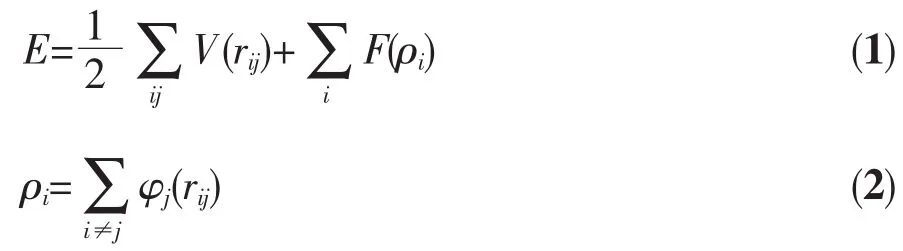
E代表体系总能量,V(rij)代表两个原子之间的对势能,F(ρi)代表体系中自由电子引起的嵌入能,ρi是 i原子上考虑了所有其他原子作用后的电子密度,φj(rij)是j原子距离其中心rij处的电子密度。纳米线中的在拉伸方向(z方向)上的平均应力(Stress)采用维里方法计算[19]:
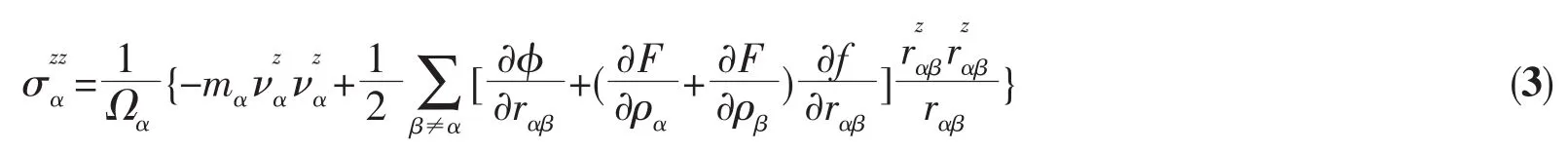
2 结果与讨论
2.1 拉伸速率对纳米线形变行为的影响
图 1a,1b和1c给出了[100]单晶铜纳米线在300 K,形变速率分别为0.02,0.2和2%·ps-1下的形变及断裂过程。从图1a可以看出,在慢速拉伸过程中,纳米线在弹性形变区内保持了体系原有的晶体结构。随着应变的增加,纳米线进入了塑性形变阶段。在500000步时 (形变ε=0.15),明显出现了沿(111)面的滑移[3,8],表现为体相原子开始向外突出,表层原子沿滑移面分开。这一现象随着应变增加表现的越来越明显。当ε=0.62时,形成明显颈缩处的原子晶格处于局域无序状态,而远离颈缩处的原子晶格保持了相对的完整性。直到ε=1.14时纳米线完全断裂。这表明了纳米线在慢速拉伸下,外力做功在Nosé-Hoover恒温处理下,能迅速将额外的动能散发掉,局域热能并不足以将原来成片的表面层原子分散。因此在平衡态拉伸条件下,表面层原子在拉伸的各个时刻均体现了与体相原子的不同,即表面层原子与体相原子之间无扩散。不过拉伸使表面积增大,新生的表面则是由体相原子外露形成。在拉伸的最后阶段,单原子线尖端部分主要由体相原子构成,具体统计结果见表1。
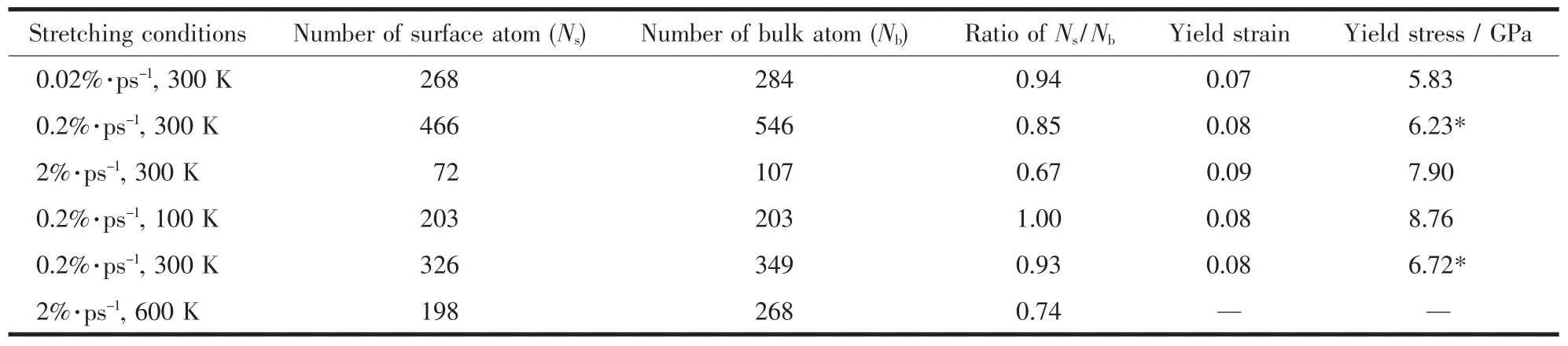
表1 拉伸条件对纳米线机械性质的影响Table 1 Effect of stretching conditions on the mechanical properties of the nanowires

图1a 纳米线在形变速率为0.02%·ps-1下拉伸过程中的形变位图Fig.1a Snapshots of copper nanowire stretching along[100]direction at the low strain rate of 0.02%·ps-1

图1b 纳米线在形变速率为0.2%·ps-1下拉伸过程中的形变位图Fig.1b Snapshots of copper nanowire stretching along[100]direction at the middle strain rate of 0.2%·ps-1
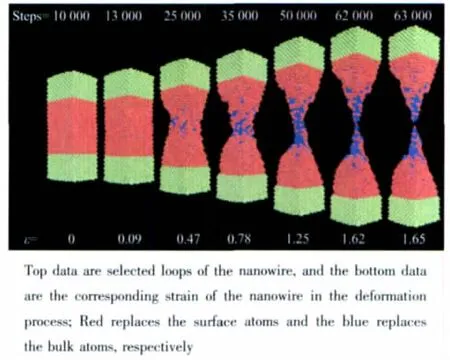
图1c 纳米线在形变速率为2%·ps-1下拉伸过程中的形变位图Fig.1c Snapshots of copper nanowire stretching along[100]direction at the high strain rate of 2%·ps-1
从图1b可以看出,纳米线在0.2%·ps-1拉伸过程中,在弹性形变区内仍然保持了原有的晶体结构。与图1a相比,可以看出纳米线在塑性形变阶段,较高的拉伸速率使沿(111)面的滑移减少。在应变ε=0.28时,体系的原子呈现了少量局域非晶态。随着应变的增加,局域非晶态的原子增加,直至ε=0.83,纳米线完全断裂。从图中可以明显看到,相对于体相原子,表面原子较为活跃,偏离平衡位置所需的能量也小于体相原子,所以表面原子总是优先于体相原子发生金属键的断裂。在此应变速率下,由于拉伸速度较快,体系虽然经过了Nosé-Hoover方法进行等温调节,但机械力做功增加了局部原子的动能,使原子排布出现混乱,表面层原子与体相原子之间扩散。此时纳米线处于准平衡态。
相对于图1a和1b中纳米线在慢速和中速的形变,纳米线在应变速率为2%·ps-1下的形变处于非平衡态拉伸。从图1c可以看出,纳米线在快速拉伸过程中,由于冲击力增加,表面原子更加活跃,最先偏离平衡位置。随着拉伸的进行,体相原子也开始呈现出无序状态并产生非晶态的原子结构。当应变ε=0.47,表面原子出现明显的破裂,这表明了高速应变速率易引起体系的局域非晶态原子增多。直至ε=1.65,纳米线完全断裂。在高速拉伸过程中,较强的机械冲击导致大量局域非晶态原子出现,表面原子与体相原子之间也表现出显著的扩散行为,从而使体系处于非平衡态。
2.2 温度效应对纳米线形变行为的影响
图2a,2b和2d给出[100]单晶铜纳米线在形变速率为0.2%·ps-1下,模拟温度分别为100,300和600 K下的形变和断裂过程。
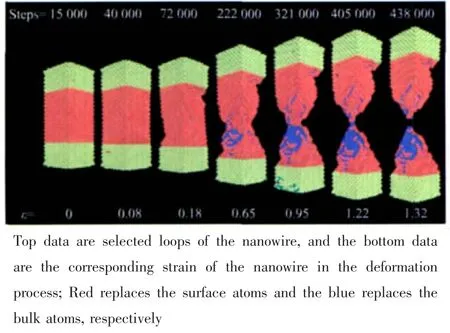
图2a 纳米线在温度为100 K下拉伸过程中的形变位图Fig.2a Snapshots of copper nanowire stretching along[100]direction at the low temperature of 100 K
从图2a可以看出,在100 K的低温拉伸过程中,纳米线在弹性形变区内保持了体系原有的晶体结构,随着应变的增加,纳米线在塑性形变过程中,明显出现表面层原子成片裂开的现象。当形变ε=0.18,纳米线出现沿(111)面滑移,体相原子开始外露;ε=0.95时,表面层原子成片裂开,晶格并未出现局域熔化状态,明显的颈缩是由滑移形成;直到ε=1.32时纳米线完全断裂。由此可得出,体系在此低温下的形变是结晶态拉伸。低温拉伸具有两个明显特征。其一,表面层原子与体相原子之间无扩散,拉伸形成的新的表面由体相原子生成。这是由于表面层原子是低配位,内聚能使原子结合稳定形成表面层。其二,由于温度低,体系一直处于结晶态,材料脆性强,表现为纳米线在拉伸过程中成块裂开。
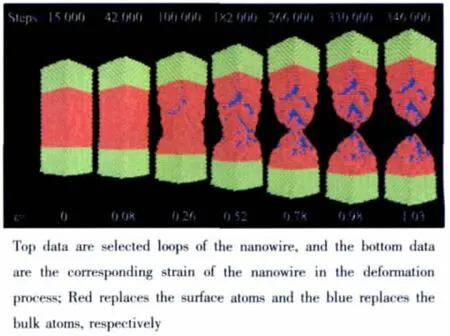
图2b 纳米线在温度为300 K下拉伸过程中的形变位图Fig.2b Snapshots of copper nanowire stretching along[100]direction at the middle temperature of 300 K
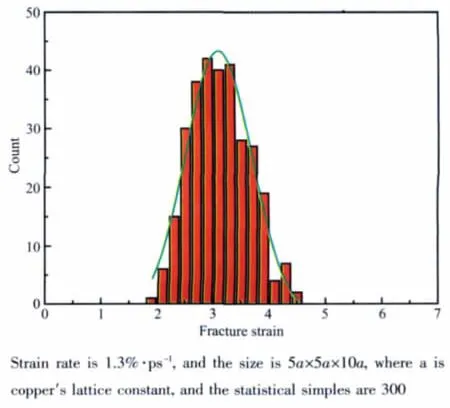
图2c 纳米线在温度为300 K下拉伸断裂时的应变统计图Fig.2c Fracture strain statistical graphic of nanowire at the temperature of 300 K
从图2b可以看出,拉伸作用下出现局域无序,滑移减少,体系的粘弹性增强,与图1b类似。在300 K,有部分的局域无序的原子簇生成。这些原子簇物质起到了一定的润滑作用,因此沿(111)面出现了明显的晶体滑移,尽管此时纳米线的绝大部分都保持极好的结晶态,但体系晶格无序度增加,降低了体系的脆性,增加了拉伸过程中的粘弹性。所以这一条件下的拉伸引起局域无序拉伸。另外,与图1b相比,在相同的应变速率和温度下,不同弛豫步数导致了纳米线最终断裂时应变不同,这可归属为纳米尺度效应导致了体系原子具有微观不确定性。由此,我们给出了5a×5a×10a(a为铜的晶格常数)的[100]单晶铜纳米线在300 K下的300个样本拉伸断裂时的应变统计分布(图2c)。应变分布采用高斯函数拟合,拟合的单峰代表了在该条件下的最可几断裂应变。
从图2d可以看出,纳米线在高温600 K的拉伸过程中,由于原子平均热运动动能增加,纳米线的原子出现了全局无序状态,表面原子和体向原子间的扩散显著,体系处于非晶态。即使在形变ε=0.03时,纳米线已呈现出无序状态;随着应变的增加,原子无序愈加明显;直到ε=1.21纳米线完全断裂。相对于100和300 K的拉伸形变,体系在高温下由低温下的结晶态拉伸转化为非晶态拉伸,从而使体系在高温下表现出显著的粘弹性。

图2d 纳米线在温度为600 K下拉伸过程中的形变位图Fig.2d Snapshots of copper nanowire stretching along[100]direction at the high temperature of 600 K
2.3 速率和温度对纳米线机械行为的影响
2.3.1 应力应变曲线
图3a和3b分别给出[100]单晶铜纳米线在不同应变速率下和不同温度下的应力应变曲线。
从图3a可以看出,在不同拉伸速率下,在弹性形变区内,应力随应变呈线性增加,在塑性形变区内,随着应变的增加,应力呈逐渐减小的趋势,直至纳米线断裂。从图中可以看到,慢速平衡态拉伸时,由于明显的(111)面滑移,应力应变曲线呈周期性波动;中速准平衡态拉伸时,由于局域无序形成的原子簇的润滑作用,曲线周期性减弱;快速非平衡态拉伸时,体系出现了大量的无序结构,无明显波动的周期性。图3a中另一个重要的特征是随拉伸速度的增加,屈服应力也随之增加,这是由于在300 K下,纳米线保持了较好的结晶状态,高速拉伸需提供额外的能量来克服体系滑移所经历的势垒。
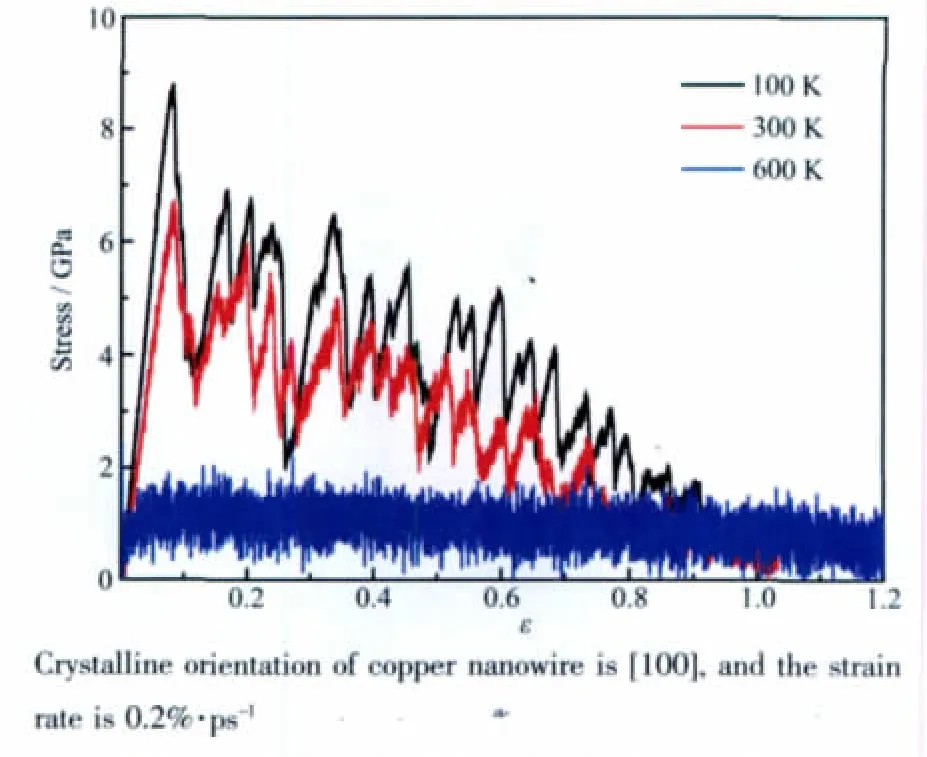
图3b 纳米线在不同温度下应力应变曲线Fig.3b Typical stress-strain curves of the nanowires at different temperatures
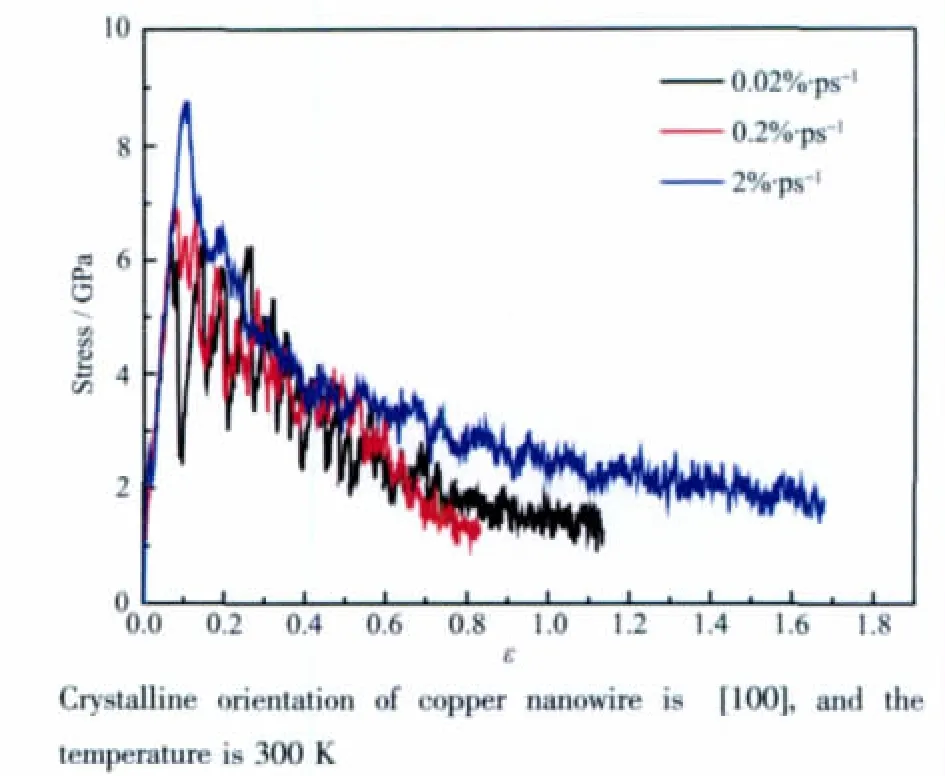
图3a 纳米线在不同速率下应力应变曲线Fig.3a Typical stress-strain curves of the nanowires at different strain rates
图3b给出了应力应变曲线随温度的变化关系。如图所示,不同的温度导致了体系的不同结晶状态,这在应力应变曲线上也得到了充分体现。低温拉伸体系保持完好的结晶状态,拉伸机理以滑移为主,因此曲线表现了较高的屈服应力,同时也具有较大的周期性应力波动。在300 K时虽然体系保留了应力的周期性波动,但相比较100 K拉伸,应力出现了显著的高频非周期性的波动。该噪音信号的波动特点体现了300 K条件下的原子无序热运动。在600 K下,体系处于非晶态拉伸,无明显屈服特征,表现了粘弹性的拉伸行为。应力应变曲线的高频无周期性,表明了体系原子在高温下剧烈振动,温度效应使原子很难处于亚稳态,从而表现了应力应变曲线高频无周期性[11,22]。
2.3.2 径向分布函数
图4a和4b分别给出[100]单晶铜纳米线在断裂时刻,不同应变速率和不同温度影响下的径向分布函数。
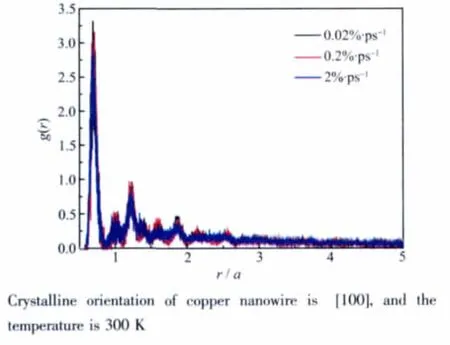
图4a 不同速率下纳米线在断裂时刻的径向分布函数Fig.4a Radial distribution function of the nanowire at the breaking point under different strain rates
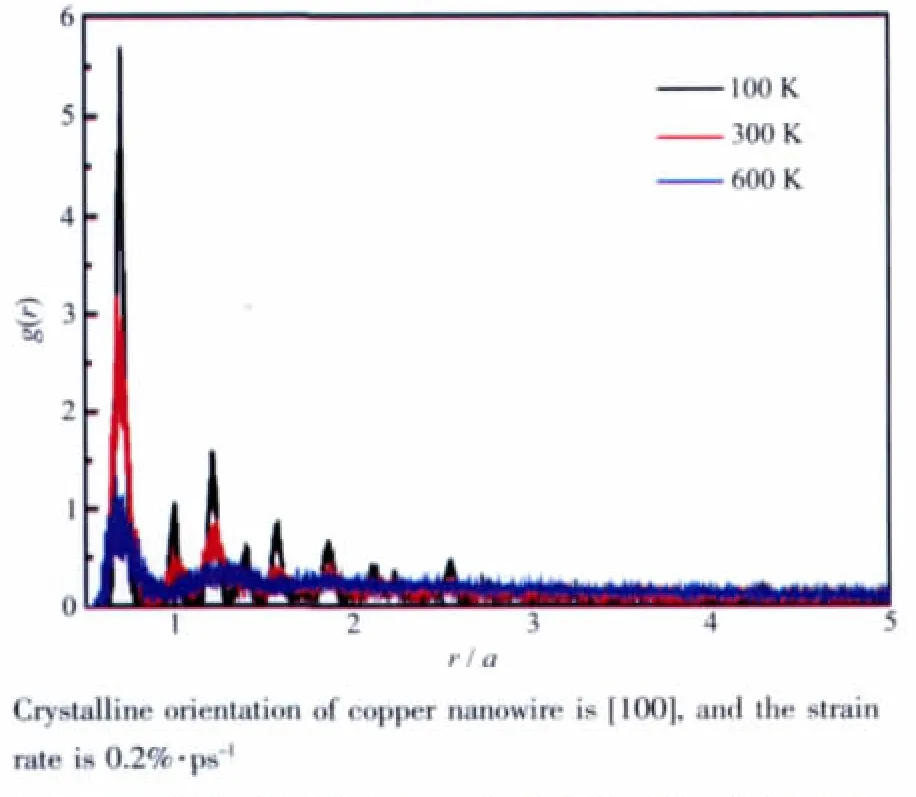
图4b 不同温度下纳米线在断裂时刻的径向分布函数Fig.4b Radial distribution function of the nanowire at the breaking point under different temperatures
从图4a中可以看出,在不同拉速下,纳米线近程有序性无明显差别。这说明,在相同的温度下,纳米线保持了一致的结晶状态。进一步证实了在不同拉伸速度下的形变和断裂的机理只与两端的冲击程度,即拉力做功功率有关。拉力导致局域无序的原子簇起到了润滑作用,促进了沿(111)面的滑移。随拉伸速度增加,体系分别处于平衡态,准平衡态和非平衡态。
而图4b则不同,径向分布函数表现了明显的温度依赖关系。第一近邻的峰值由100 K的5.7降至600 K的0.9。其他几个近邻原子数也表现了同样的下降趋势。此外,对于600 K的径向分布曲线,除第一近邻外,其他峰明显宽化,说明体系近程无序,即体系原子处于非晶态。图4b充分说明升温改变了体系的结晶状态,从而导致拉伸形变机理的差异,也导致纳米线机械力学性质的不同。
2.3.3 能量曲线
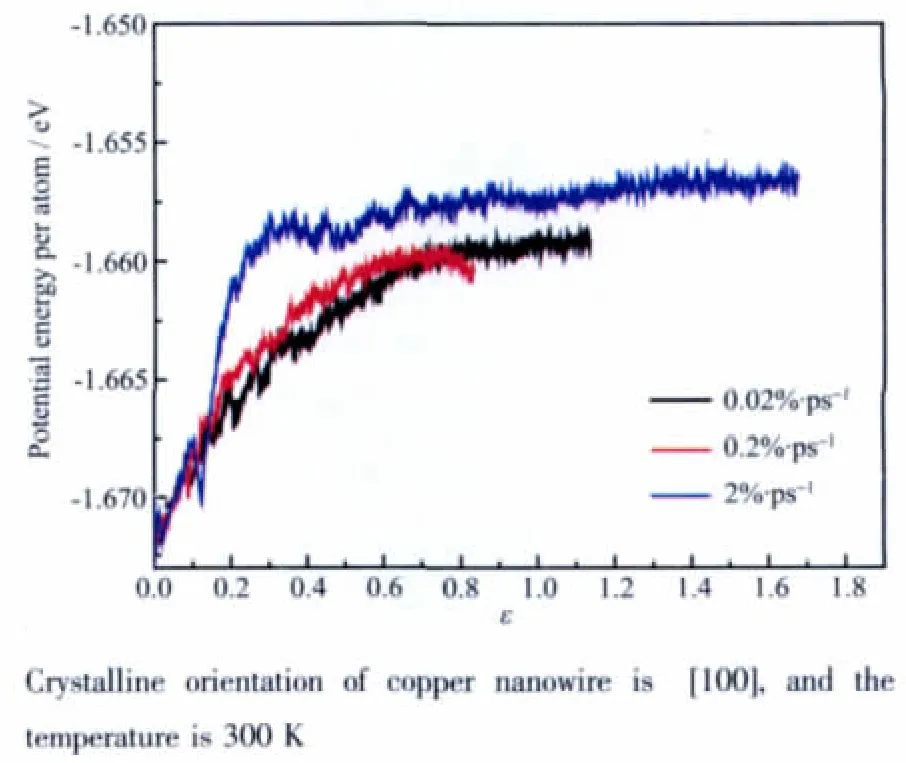
图5a 纳米线在不同拉速下的能量曲线Fig.5a Energy curves of the nanowires at different tensile strain rates
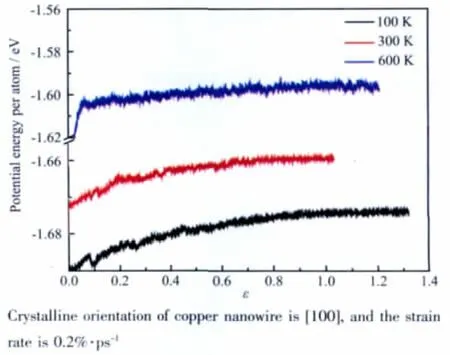
图5b 纳米下在不同温度下的能量曲线Fig.5b Energy curves of the nanowires at different temperatures
图5a和5b别给出[100]单晶铜纳米线在不同应变速率和不同温度下的原子平均势能曲线。从图5a中可以看出,在应变为0时,3条曲线具有相同的势能起点。随着应变增加势能呈上升趋势,并且在低速和中速时势能的上升相对平缓。而在高速时,纳米线的势能急剧增加,之后达到一个相对平稳的状态。比较可知,在纳米线的整个形变过程中,原子的最大平均势能随着应变速率的增加而增大。这说明较高应变速率导致更大的机械冲击从而使原子的平均势能增加,这与纳米线的滑移的形变机理是一致的。
图5b是单晶铜纳米线分别在不同温度100,300和600 K下的原子平均势能曲线。在应变为0时,平均势能分别为-1.69,-1.68,-1.66 eV。说明在纳米线的拉伸形变的初期,不同温度导致了不同的原子晶格振动程度。在较低温度下,原子在平衡位置轻微振动,晶格有序性好。随着温度升高,原子晶格振动加剧,原子的晶格有序性变差,从而导致了纳米线的原子势能增加。在100 K,原子的势能在应变为0.1时,势能出现了明显降低,这与图3b中的应力应变屈服循环一致。在高温600 K时,原子的平均势能在应变为0.1时急剧增加,之后随着应变增加势能达到一个相对平稳的波动状态,与其无屈服行为一致。另外,在图5a和5b中,相比块体材料铜在0 K下的势能(-3.5 eV左右),纳米线体系的原子平均势能均在-1.7 eV以上,这归属为纳米尺度下表面效应引起了体系的平均势能的增加。
3 结 论
利用分子动力学模拟我们考察了沿[100]晶向铜纳米线的拉伸行为。不同的拉伸速度使体系分别处于平衡态,准平衡态和非平衡态拉伸。表面原子与体相原子的扩散也随之加剧。而升高温度,体系由结晶态向非晶态过渡,材料性质也由脆性向粘弹性转变。
[1]Rubio-Bollinger G,Bahn S R,Agraït N,et al.Phys.Rev.Lett.,2001,87(26):266101
[2]Ekinci K L,Roukes M L.Rev.Sci.Instru.,2005,76(6):061101
[3]Finbow G M,Lynden-Bell R M,McDonald I R.Mol.Phys.,1997,92(4):705-714
[4]Hemker K J.Science,2004,304:221-223
[5]Agrait N,Rubio-Bollinger G,Vieira S.Phys.Rev.Lett.,1995,74:3995-3998
[6]Sun C Q.Prog.Solid State Chem.,2007,35:1-159
[7]Ikeda H,Qi Y,Cagin T,et al.Phys.Rev.Lett.,1999,82:2900-2903
[8]Koh S J A,Lee H P.Nanotechnology,2006,17:3451-3467
[9]Ikeda H,Qi Y,Cagin T,et al.Phys.Rev.Lett.,1999,82:2900-2903
[10]Branício P S,Rino J.Phys.Rev.B,2000,62:16950-16955
[11]Koh S J A,Lee H P,Lu C,et al.Phys.Rev.B,2005,72:085414
[12]Hoover W G.Phys.Rev.A,1985,31:1695-1697
[13]Nosşe.Mol.Phy.,1984,52:255-268
[14]Nosşe.J.Chem.Phy.,1984,81:511-519
[15]Zhao J W,Yin X,Liang S,et al.Chem.Res.Chin.Univ.,2008,24:367-370
[16]Johnson R A.Phys.Rev.B,1988,37:6121-6125
[17]Johnson R A.Phys.Rev.B,1988,37:3924-3931
[18]Johnson R A.Phys.Rev.B,1989,39:12554-12559
[19]Wu H A.Eur.J.Mech.a-Solids,2006,25:370-377
[20]ZHAO Jian-Wei(赵健伟),WANG Fen-ying(王奋英),JIANG Lu-Yun(蒋璐芸),et al.Acta Phys.Chim.Sin.,2009,25(9):1835-1840
[21]Zhao J W,Murakoshi K,Yin X,et al.J.Phys.Chem.C,2008,112:20088-20094
[22]Wang F Y,Liu Y H,Zhu T M,et al.Nanoscale,2010,2(12):2818-2825
[23]Wang F Y,Liu Y H,Yin X,et al.J.Appl.Phys.,2010,108(7):074311
[24]Wang D X,Zhao J W,Hu S,et al.Nano Lett.,2007,7(5):1208-1212
[25]Liu Y H,Wang F Y,Zhao J W,et al.Phys.Chem.Chem.Phys.,2009,11(30):6514-6519
[26]Liu Y H,Zhao J W,Wang F Y.Phys.Rev.B,2009,80(11):115417
The Effects of Strain Rate and Temperature on the Deformation Behavior of the Single-Crystal Copper Nanowire
ZHU Tie-Min2,3HOU Jin*,2,3WANG Fen-Ying1GAO Ya-Jun1ZHAO Jian-Wei*,1,2
(1Key Laboratory of Analytical Chemistry for Life Science,Ministry of Education,School of Chemistry and Chemical Engineering,Nanjing University,Nanjing 210008,China)(2School of Information Science and Technology,Southwest Jiaotong University,Chengdu 610031,China)(3State Key Laboratory for Novel Software Technology,Nanjing University,Nanjing 210093,China)
Molecular dynamics simulations were used to study the deformation behaviors of the [100]singlecrystal copper nanowire subjected to uniaxial tension.The tensile strain rates are 0.02%·ps-1,0.2%·ps-1and 2.0%·ps-1,and the simulated temperatures are 100,300 and 600 K,respectively.The deformation behaviors,mechanical property,radial distribution function and the energy curve were studied in detail.The results show that the deformation of the nanowire at low,middle and high strain rates correspond to the equilibrium,quasiequilibrium and non-equilibrium states,respectively.The structure reveals crystalline,local disorder and amorphous forms at low,middle and high temperature,respectively.
molecular dynamics;nanowire;crystalline state;local disorder
O614.121
:A
:1001-4861(2011)05-0928-07
2011-01-14。收修改稿日期:2011-02-23。
国家自然科学基金(No.20821063,20873063,51071084),国家重点基础研究发展计划(973项目)(No.2007CB936302,2010CB732400),江苏省自然科学基金(No.BK2010389),高等学校博士学科点专项科研基金(No.20070284007),教育部留学回国人员科研启动基金,2009年高等学校博士学科点专项科研基金(No.20090184120022)以及中央高校基本科研业务费专项资金科技创新项目(No.SWJTU09CX036)资助项目。
*通讯联系人。 E-mail:zhaojw@nju.edu.cn,jhou@swjtu.edu.cn

