西藏自治区科技进步贡献率的测算与预测:1990—2015
朱 帆,余成群,董冠鹏
(1.中国科学院地理科学与资源研究所,北京 100101;2.中国科学院研究生院,北京 100039)
西藏自治区科技进步贡献率的测算与预测:1990—2015
朱 帆1,2,余成群1,董冠鹏1,2
(1.中国科学院地理科学与资源研究所,北京 100101;2.中国科学院研究生院,北京 100039)
本文以Cobb-Douglas为核心,以西藏自治区1990—2008年的统计数据为基础,综合运用最小二乘法、势分析法、调整法和经验法估计出资本和劳动力产出弹性。继而运用索洛余值法测算和预测1990—2015年西藏自治区的科技进步贡献率。计算结果表明,西藏自治区科技进步贡献率稳步上升,2008年达到了30.8%,预计2015年达到40.7%,但投资拉动特征明显。最后,基于测算与预测结果向自治区有关部门提出相关建议。
科技进步贡献率;索洛余值法;最小二乘法;势分析法;西藏
1 引言
科技进步贡献率测算是当代计量经济学领域的一个热门研究话题。西方的科技进步测定模型主要有 4 种[1]:索洛(R.M.Solow)于 1957 提出的余值法(SR);阿罗(Arrow)于1961年提出的常数替代弹性(Constant Elasticity of Substitution,CES)生产函数模型; 克里斯丁森 (L.Christensen)、 乔根森(D.Jorgenson)和莱恩(L.Lane)于1973年共同提出的超越对数生产函数;美国经济学家丹尼森(E.F.Denison)于1962年提出的丹尼森模型。
从20世纪80年代开始,国内掀起了一股研究科技进步贡献率的热潮。2006年,国务院在《国家中长期科学和技术发展规划纲要》中进一步明确提出全国科技进步贡献率要在2020年达到60%,以及在2010—2020年期间确保科技进步年均增长率在4.53%基础上不断提高的总目标。此后,各省市也相继在各自的科技中长期发展规划中对该指标加以量化。西藏自治区“十二五”规划编制在即,为了给相关部门提供决策参考,了解和掌握自治区各历史时期和未来一段时间内科技进步贡献率的变化情况是非常必要的。
鉴于之前有关省域科技进步贡献率测算的研究更偏重于结果,缺乏对于统计学过程的探讨,故本文以广义的科技进步概念和索洛余值法为基础,对西藏自治区科技进步贡献率进行测算的过程中,尝试将方差膨胀因子、B-P值和K-S值等更为严格的统计检验方法,以及势分析法引入到弹性系数修正中。所谓广义的科技进步,即将经济增长的源泉除了资本和劳动力的投入之外,皆统称为“科技进步”或者“全要素”[2]。在上述基础之上,借助多元回归拟合预测“十二五”期间西藏自治区的科技进步贡献率,以期为西藏“十二五”规划乃至今后相关领域的科技进步贡献率测算工作提供有益借鉴。
2 测算与预测原理
鉴于索洛余值法目前仍是国内外最有影响、最广泛使用的测算科技进步贡献率的方法[3],且原国家计委和国家统计局把索洛余值法作为各省区市测算科技进步贡献的标准方法进行推广[4],本研究亦采用索洛余值法作为西藏自治区1990—2008年科技进步贡献率实证数据测算的核心方法,以此增加测算结果的可信度和横向可参照性。
索洛余值的核心仍然是基于C-D生产函数[5]:

两边同时取自然对数,进而对时间t求导数,并设k=lnKt,l=lnLt即可得到索洛增长速度方程:

其中:y为产出增长速度,k和l分别为资本和劳动力的增长速度,c为科学技术进步的年均增长速度;ak、βl分别为资本和劳动对经济增长的贡献份额。根据定义,经济增长速度中科技进步因素所占的比重即科技进步贡献率,则其对应的测算公式为:

2009—2015年的西藏自治区科技进步贡献率预测主要基于多元回归拟合法,方法标准且操作简单,在此不再赘述。
3 指标选取
依据国家部委推荐的标准算法,本文主要在时间序列上考虑三个指标:产出量Y、资本投入量K和劳动投入量 L[6]。
(1)产出量 Y。
以西藏自治区1990—2008年的名义地区生产总值(GDP)为基础数据,通过地区生产总值指数将其换算成为以1990年可比价格为基础的实际GDP。
(2)资本投入量 K。
由于资本投入和社会经济效益的产出在时间上存在“时滞”,因此本文采用资本存量而非当年固定资产投资额作为测度变量。资本存量的测算采用Goldsmith于1951年创立的永续存盘法[7],基本公式为:

其中:Kt为第t年的资本存量,It为第t年的固定资产投入,按照王小鲁[8]等权威学者的建议,采用西藏自治区全社会固定资产投资表征资本流量,Pt表示固定资产投资价格指数,δ为固定资产折旧率。
(3)劳动投入量 L。
采用全社会历年从业人员数作为劳动投入的度量。
4 弹性系数α和β的确定
科技进步贡献率测算所需弹性系数的确定主要基于最小二乘法(OLS)、势分析法和调整法,并由经验估计法最终确定。
4.1 基于OLS估计的弹性系数确定
首先利用丁伯根改进型C-D生产函数测算资本的产出弹性α和劳动力产出弹性β。丁伯根改进型C-D生产函数为:
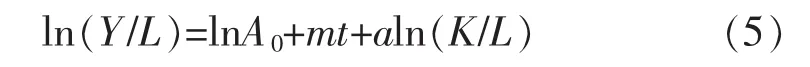
将ln(Y/L)视为模型因变量,把年份 t和ln(K/L)视为模型自变量,运用matlab进行OLS测算。对于测算结果,运用GLS估计消除时间序列问题,经过F检验、序列相关检验、方差膨胀因子检验、异方差检验和残差正态性的K-S检验保证所得弹性系数的统计学有效性。
4.2 基于势分析法的弹性系数确定[9]
势分析法同样是基于西方经典的Cobb-Douglas生产函数:

引入表示资金投入和劳动投入发挥效能程度的势效系数r1和r2,得到改进的生产函数:

其中:P1=Y/K为报告期资金产值率,P2=Y/L为报告期劳动生产率,p01和p02分别为基期资金产值率和劳动生产率(一般取前一年为基期)。规模报酬不变假设下,α+β=1。α、β是时点函数,与样本大小及样本均值无关。
为了解得α和β的时点解,引入条件:

则基于势分析法的弹性系数α和β的测度公式为:

4.3 基于调整法的弹性系数确定
原国家计委、统计局综合全国情况,建议全社会资本产出弹性设定为0.35。但考虑到我国地理分异特征明显,且西藏自治区的区位和自然条件极其特殊,故依据国家统计局推荐的弹性系数调整公式,结合西藏自治区的实际情况,采用对资金产出弹性和劳动产出弹性系数的修正值 a*[10]:

Kt、Lt表示西藏自治区第t年的资金存量和劳动力,K0t、L0t表示全国第t年的资金存量和劳动力。修正的劳动力弹性系数:β*=1-a*。
4.4 基于经验法的弹性系数确定
经验法主要依据同西藏自治区相关领域专家的探讨,通过加权平均处理得出最终弹性系数取值。本研究所采用的加权平均公式为:

其中xi为运用不同方法得到的资本产出弹性,而wi为结合区域实际情况人为赋予各个资本产出弹性的权重值,且不同资本产出弹性的权重值相加为1。
5 西藏自治区1990—2008年科技进步贡献率的实证数据测算
5.1 数据准备
自治区GDP、全社会从业人员数来源于《西藏统计年鉴2009》。1990—2008年资本存量来自于历年《中国农村统计年鉴》。在资本投入的测度过程中,由于西藏自治区没有固定资产投资价格指数,本研究采用GDP平减指数进行平减处理[11],基年资本存量按照基年全社会固定资产投资乘以3得到[12],而折旧率选取张军[13]推荐的9.6%。为保证数据统一,产出Y和资本投入K以亿元为单位,并按1990可比价格进行计算,而劳动投入量L以万人计。篇幅所限,本文仅列出2000—2008年的西藏自治区可比价格投入产出数据(表1)。
需特别指出的一点是,由于科技对经济增长的贡献具有滞后性、长期性和一定的周期性,其作用大小与经济周期和科技自身发展的规律有关[14]。科技自身的发展(重大科学发现和技术发明)需要一个储备过程,科技对经济增长的贡献也有一个积累过程[15],加之索洛模型自身的局限性,较短时间尺度下的科技进步贡献率测算结果往往波动剧烈、失真,甚至有时会出现十分“荒谬”的结论[16]。鉴于此,本研究在进行年度科技进步贡献率测算时,对统计数据采用3年滑动平均处理[17]。但是经过滑动平均得到的数据集排除了时间序列端点上的数据,即1990年和2008年的统计数据。为了将1990年和2008年作为样本进行估计,进而增加估计的合理性,采用统计插值的方法补充1989年和2009年的时点数据。

5.2 弹性系数α和β的确定
在规模报酬不变(α+β=1)的假设下,本文测度资本弹性系数α和劳动力弹性系数β时综合运用了OLS回归法、势分析法、调整法和经验法,以期互相验证。
(1)基于OLS回归法的弹性系数估计。
在对(5)式进行 OLS回归并借助GLS消除时间序列影响之后,最终得到的丁伯根改进型C-D生产函数为:

严格的回归检验(表2)说明最终调整得到的函数已不存在序列相关、共线性、异方差和非正态分布问题,具有良好的统计学品质,得出的资本弹性系数 α(0.195)和劳动弹性系数 β(0.805)亦具有较高的统计学置信度。

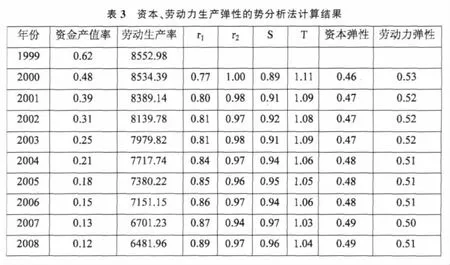
(2)基于势分析法的弹性系数确定。
在势分析法确定弹性系数的过程中,利用经过平滑处理的统计年鉴数据(表1)得到的每年的资金和劳动力生产弹性,其过程及结果见表3,这里α取历年的均值0.48,劳动力弹性β为0.52。
(3)基于调整法的弹性系数确定。
将平滑处理的数据(表1)带入(8)式即可得出最终的资本弹性系数α(0.44)和劳动力弹性系数 β(0.56),在此不再赘述。
(4)基于经验法的弹性系数确定。
在专家讨论的基础之上,结合上述资本弹性系数的统计学测度结果以及世界银行对东亚国家社会经济情况的定性描述[18],我们将西藏自治区资本弹性系数的上限设定为0.5,下限采用之前OLS估计的0.195。最后,在0.01的统计学可置信前提之下,本文将通过加权平均(表4)得出的资本劳动力弹性系数作为测算西藏自治区科技进步贡献率的最终弹性系数取值。
表4中,鉴于势分析法和调整法得到的资本弹性系数较为接近(0.44和0.48),且经济学意义皆好其他估计值,更符合西藏自治区的情况,因此我们为其赋予的权重最大(0.35),经验估计得出的西藏自治区资本弹性系数上限次之(0.25),而OLS估计值由于其特定环境下的经济学意义欠佳,尽管统计学置信度很高,但是最终赋予的权重最小(0.05)。依据(9)式,最终的资本弹性α取0.48,相应的劳动力弹性系数 β 为 0.52(β=1-α)。

5.3 西藏自治区科技进步贡献率测算
基于最终确定的资本产出弹性系数α(0.48)和劳动力产出弹性系数β(0.52),通过计算资本存量和产出的增长率,利用(3)式得到资本、劳动力、科技进步贡献率的数值(表5)。
各要素贡献率的相对结构如图1。

6 西藏自治区2009—2015年科技进步贡献率预测
为预测2009—2015年西藏自治区的科技进步贡献率,本文采用1990—2008年的数据进行回归拟合,首先预测出该时间段西藏自治区GDP、资本存量和劳动力平均增长率(表6)。
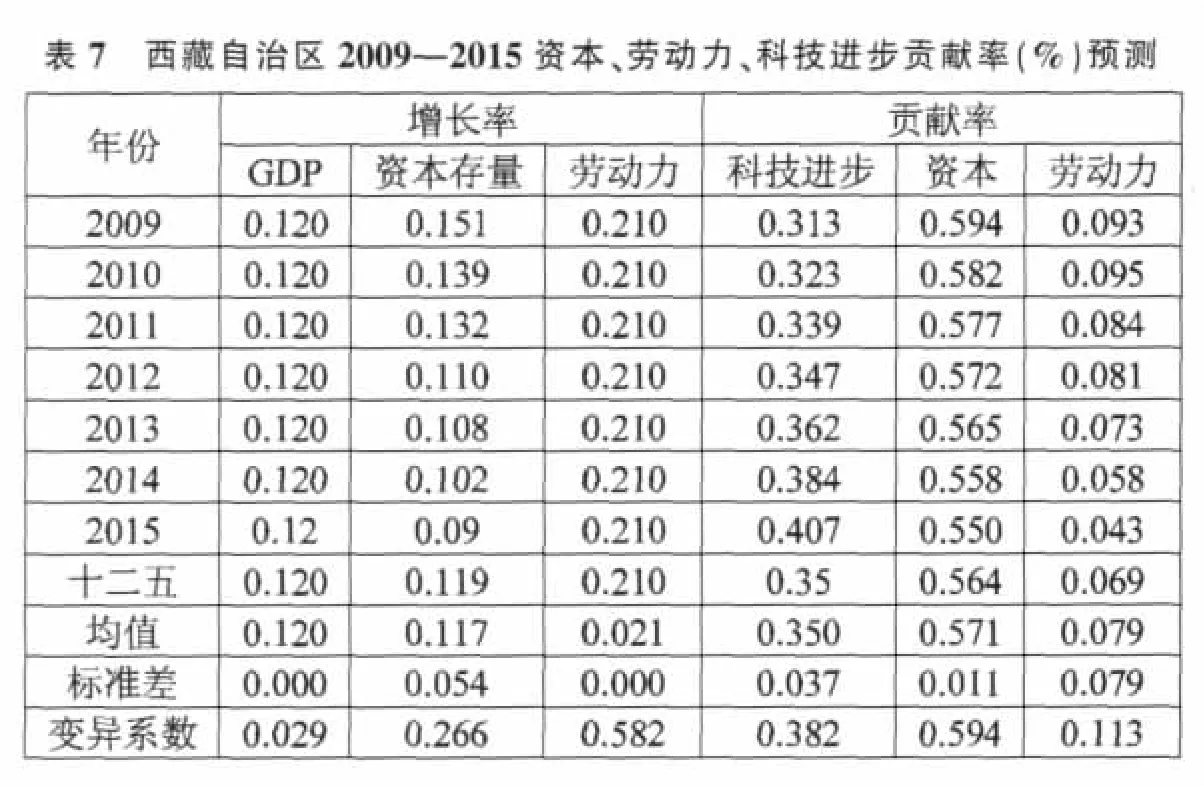
根据上文对西藏自治区地区生产总值、资本存量和劳动力总量增长率的预测,根据(2)式和(3)式可以得到“十二五”期间及各年份的资金、劳动力和技术进步贡献率(表7)。
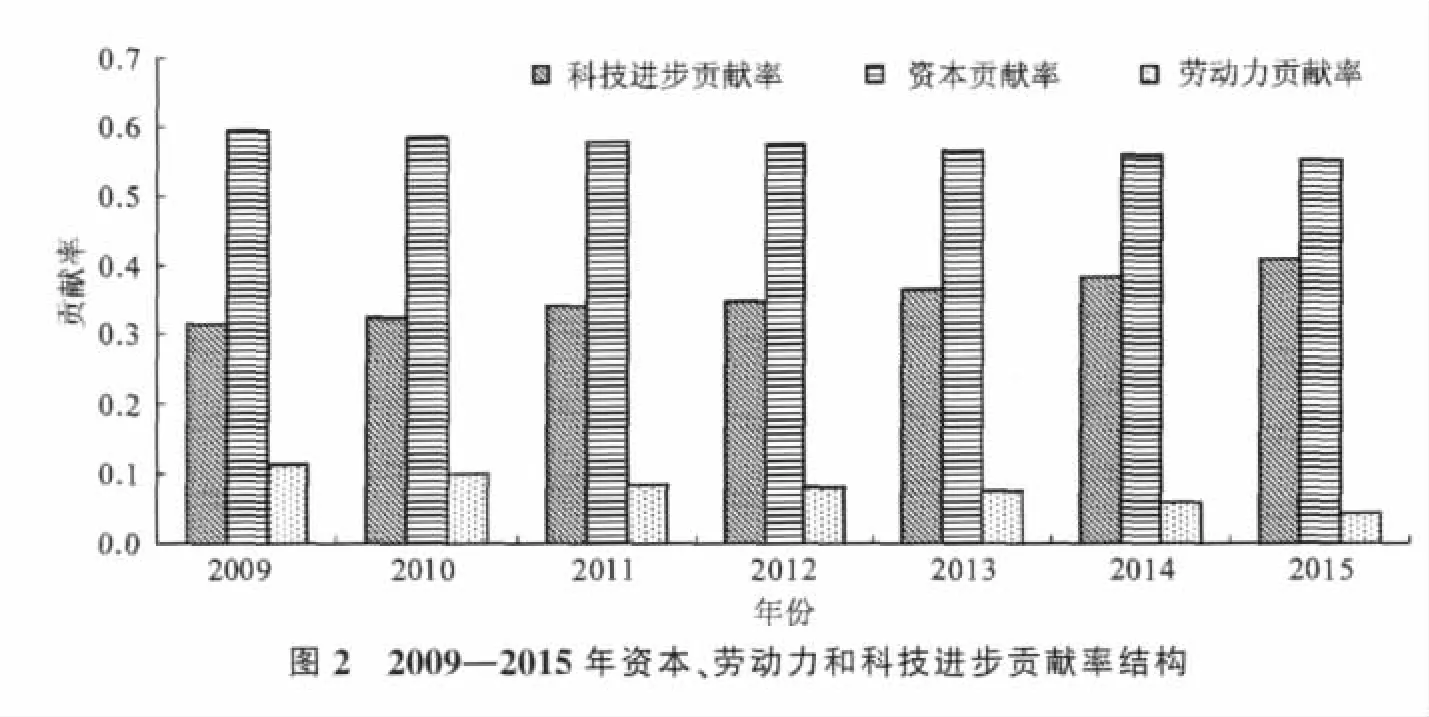
各要素贡献率的相对结构如图2。
7 分析与建议
从西藏自治区科技进步贡献率的测算和预测结果来看,“十一五”头三年的科技进步贡献率(25.7%)远高于“十五”期间的相应指标(6.9%),2015年这一数值更可以达到40.7%,并保持年均4.12%的增长率;资本存量贡献率在2000—2008年整体上呈现下降的趋势,说明西藏自治区已经慢慢走出较单纯依靠投资拉动的粗放的经济增长方式[19];劳动力贡献率在2000—2005(即“十五”期间)间整体呈现缓慢上升的趋势,但2006年以后的“十一五”期间又出现下滑趋势,这一现象符合经济增长的一般规律:随着资本深化、科技发展起势,技术进步,劳动力数量增长对经济增长的拉动作用将越来越小。同时,这也再次印证了资本存量贡献率所体现出的西藏社会经济发展趋势:西藏自治区已经慢慢走出依靠投资拉动的粗放的经济增长方式,逐步走向提高资本利用效率的集约型经济增长方式[20]。
上述这一切无疑都是一个个巨大的成就,但从拉动经济增长的各要素的贡献结构中,资本存量目前仍占据主要地位,2008年资本贡献率占61.1%,而2000—2008年资本贡献所占的平均份额更是达到了81.8%,这说明投资不仅在过去,而且在未来的一定时期内还将是拉动经济增长的最主要因素。
更为严峻的是,从模型预测的发展趋势来看,西藏自治区科技进步贡献率在2020年达到 《国家中长期科学和技术发展规划纲要(2006—2020)》中所提出的全国平均水平(60%)和年均增长率(4.53%)几乎是不可能的。换言之,西藏自治区常规的“科技进步”很可能难以支撑西藏的“跨越式发展”。鉴于此,从提升科技进步贡献率的角度而言,建议西藏自治区加大以下两个方面的工作力度:
(1)实施西藏科技工作的超常规、大跨越发展战略。按照科技进步贡献率的计算公式,贡献率的大小同科技进步增长速度成正比,提高科技进步增长速度就是直接提高了科技进步贡献率。要提高科技进步增长速度,最重要的就是从“十二五”开始实施超常规的科技“跨越式发展”,并将“十一五”确定的“支撑发展”的科技战略改为“支撑跨越”的科技发展新战略。
(2)持续地、大幅度地增加科技投入。科技要超常规发展,必须要有超常规的投入来加以支撑。加强研发投入,是提高科技进步贡献率,推动科技进步和自主创新的重要支持手段。发达国家研发投入占GDP的比重一般都在2%以上,而从科技统计年鉴数据来看,2008年国内部分发达省份(直辖市),如北京、天津、上海、江苏和广东等,研发投入占GDP比重接近甚至超过了2%,而西藏自治区该指标在2008年仅有0.26%,支持发展尚显后劲乏力,更无法达到支撑跨越的要求。

[1]陈颖,李强.索洛余值法测算科技进步贡献率的局限与改进[J].科学学研究,2006,(24):23-40.
[2]Denis C,McMorrow K.An analysis of EU and US productivity developments [R].European Comumities,2004,232-298.
[3]Effrey M Woodridge.Introductory Econometrics(Third Edition)[M].China Renmin University Press,2007,286-377.
[4]龚三乐.科技进步贡献率测算研究综述[J].怀化学院学报,2008,(11):29-31.
[5]Robert M solow.Technical Change and the aggregate production function [J].Review of Economics and Statistics,1957,39(3):312-320.
[6]郭庆旺,贾俊雪.中国全要素生产率的估计:1979—2004[J].经济研究,2005,(5):15-23.
[7]Raymond W Goldsmith.A perpetual Inventory of National Wealth[J].Studies in Income and Wealth,1951,14(3):5-74.
[8]王小鲁,樊纲.中国经济增长的可持续性[M].北京:经济科学出版社,2000.
[9]贾雨文,李荣平,王国贞,宋艳涛.弹性系数调整和贡献率算法的改进[J].数量经济技术经济研究,1997,(4):21-24.
[10]李宾,曾志雄.中国全要素生产率变动的再测算:1978—2007[J].数量经济技术研究,2008,12(8):37-42.
[11]曹吉云.我国总量生产函数与技术进步贡献率[J].数量经济技术经济研究,2007,11(8):11-17.
[12]黄勇峰,任若恩,刘晓生.中国制造业资本存量永续存盘法估计[J].经济学(季刊),2002,(3): 21-29.
[13]张军.对中国资本存量 K 的再估计[J].经济研究,2003,(7):8-19.
[14]Schultz T W.Investment in human capital[J].American Economic Review,1961,51(1):1-17.
[15]Gerlach S,M Yiu.Estimating output gaps in Asia:a cross-country study [J].Journal of the Japanese and International Economies,2004,1(8):115-136.
[16]李治国,唐国兴.资本形成路径与资本存量调整[J].经济研究,2003,(5):33-41.
[17]Kydland F and E Prescott.Time to Build and Aggregate Fluctuations[J].Ecomomentrica,1982,10(5):1354-1370.
[18]World Bank.The East Asian Miracle:Economic Growth and Public Policy [M].New York:Oxford University press,1993.
[19]Musso A and T Westermann.Assessing potential output growth in the Euro area-a growth accounting perspective[A].European Central Bank,Discussing Paper Series[C],2005,22(3).199-214.
[20]Scheibe J.The Chinese Output Gap During the Reform Period 1978—2002 [R].Oxford: Department of Economics Discussion Paper No.179,University of Oxford.
(责任编辑 刘传忠)
The Calculation and Forecast of the Contribution Rate of Scientific and Technological Progress in Tibet
Zhu Fan1,2,Yu Chengqun1,Dong Guanpeng1,2
(1.Institute of Geographic Sciences and Natural Resources Research,Chinese Academy of Sciences,Beijing 100101,China;2.Graduate University of Chinese Academy of Sciences,Beijing 100039,China)
Based on the statistics from 1991 to 2008 in Tibet Statistical Year book and using the Cobb-Douglas production function growth calculation model,this paper firstly gets the capital-output and labor-output flexibility by means of ordinary least squares,potential analysis,adjustment method and empirical method.On this basis,the contribution rate of scientific and technological progress from 1990 to 2008 in Tibet is calculated through Solow residual value.The research indicates that the contribution rate of scientific and technological progress of Tibet is rising among fluctuation,reaches about 30.8%in 2008 and 40.7%in 2015.However the problem of independence on investment input still exists.Finally,this paper proposes some policy recommendations to raise the contribution rate of scientific and technological progress of Tibet.
the contribution rate of scientific and technological progress; Solow residual value; OLS; potential analysis; Tibet
F062.3
A
国家科技支撑计划项目(2007BAD80B03)。
2010-06-03
朱帆(1985-),男,河北石家庄人,中国科学院地理科学与资源研究所硕士研究生;研究方向:区域可持续发展。

