测量不确定度评定应基于误差理论
林洪桦
(北京理工大学机械与车辆工程学院)
1 概述
《测量不确定度指南》ISO 1993(E)[1](简称GUM)颁布至今几近廿载,对于我国使用和评定测量不确定度起到了促进和规范化的作用。尤其在计量基准和标准的建立、量仪检定、各种计量技术法规的制定等方面更有利于国际比对及与之接轨。尽管在此期间与其相关的标准和技术规范都曾作过修订和补充,然而均未做出本质性更改,而只是完善和增补了些术语和定义、更明确了适用范围、添加了应用技术等。GUM(ISO/IEC Guide98-3-2008)以及我国报审的JJF1059.1 《测量不确定度评定与表示》均基于误差理论,且是在国内外有关专家继承、发展测量误差及数据处理基础上,经“求同存异”而商讨的结果,因而在GUM实施中不免会有不同的见解和异议,也包含误差理论发展上要求扩展应用GUM的问题。
作者自1962年从事测量误差与数据处理的教学与科研以来,就一直在探讨误差的量化表示方法。在GUM 颁布之前的一些征求意见的讨论中,就已认为测量不确定度实质上是测量误差的一种规范性量化形式,有利于量值准确度的国际比对。GUM 颁布之时又恰在误差分类不一、误差估算与合成方法众说纷纭的发展阶段,GUM 的颁布及时地取得了统一一致的规范化效果。然而,GUM ISO 1993(E)版本仍然不免存在某些矫枉过正之弊,如免用真值、不涉及误差、不主张误差,按其性质分类:系统误差和随机误差等等,引起当时科技界专家和学者对GUM理解的差异,甚至是错误见解,如将不确定度与误差对立起来。尽管经过GUM不断贯彻实施以及修订和补充,已渐统一认识,但仍不免有些异议。
可见,捋清测量不确定度评定与误差理论关系,仍是当前值得论述的问题。下面在作者编著的“测量误差与不确定度评估”[2]中有关论述的基础上,再作如下的归纳。
2 测量不确定度与真值和测量误差
无论以往还是现今,对于测量不确定度的定义都是指表征赋予被测量值分散性的非负参数。显然,这里可以不涉及真值,也避免了测量误差定义为测量结果减去被测量真值而引起的不可确定性,却并无法表明不确定度与真值、误差的关系。
首先,测量不确定度的来源:被测量定义及其体现;计量基准或标准件;测量设备;测量方法;测量环境条件;测量人员等方面,几乎与传统上分析测量误差来源完全一致。也可以说,这是继承了测量误差来源分析经验的结果。
其次,测量不确定度评定是在已修正显著系统影响且不计及异常值的条件下进行。这样的前提条件,实质上都不免应针对被测量真值而言。显然,被测量值的分散性可以围绕着或接近于真值而分散,也可能远离其真值而分散。在实现定量化分析中真值多以约定真值来替代,也都需要继承、吸取传统系统误差和粗大误差的分析、估计和识别经验。
问题在于对误差定义的理解上有些绝对化。在测量中,测量误差Δx定义为被测量的测量结果减去被测量的真值x0,即Δx=-x0。而x0却是待定的未知真实值,因而误差似乎就是难以确知的。其实误差历来都是针对无误差的目标值定义的,只不过应予合理地规范化定量表示而已。传统的误差理论上对测量结果的表示为:其中为测量数据的均值;Δ0为系统误差修正值(针对真值/约定真值做出的估计);Δlim为极限误差。通常Δlim= k s+∑iei,前项为测量数据的k倍标准差;后项为剩余系统误差、先验随机误差等等的总和。这与GUM中所论述的不确定度评定方法并不存在本质性矛盾。
因此,不确定度评定不仅不应与误差理论割裂,反而应继承且依据传统的误差理论及其发展现状。同时,也不可能完全避开真值和测量误差,应视为测量误差在已修正显著系统误差,且经识别并剔除异常值后,关于被测量值分散性的一种规范化定量表示形式。以下的几点继续论述将更有力地支持这种统一一致的论点。
3 测量不确定度评定方法与误差分类
不确定度评定强调可操作性,且在GUM中提出了两类评定方法:对测量列用统计分析的A类评定与其它不同于A类的B类评定(列举出了一系列B类评定的提示性方法),且均以标准差来定量表示不确定度u,又表明无需予以严格区分。同时指出,这两类评定方法并不对应着随机误差、系统误差两种分类,这无疑有利于对被测量值分散性做出规范化定量表示。尽管这种分散性中含有随机性影响因素,也含有已修正显著系统影响后剩余系统性影响因素,却无需纠缠其起因。
然而,误差来源不同对测量结果影响就各异。在误差理论中,传统上对误差按其性质不同划分为两类:系统误差和随机误差。前者指的是对同一量多次测量过程中,保持恒定或以可预知方式变化的测量误差分量,并定义为在重复性条件下对同一被测量进行无限多(或足够多)次测量结果的平均值减去被测量的真值;后者则是以不可预知方式变化的测量误差分量,并定义为测量结果减去在重复性条件下对同一被测量进行无限多(或足够多)次测量结果的平均值。这种分类既是客观存在也是应予认知的。以往存在定量化与估计形式不一致问题,尤其系统误差定量化分析、估计主要依赖于专业技能,“个性”强而共性弱,难有普适性方法可循。这也就是造成误差量化指标(如随机性系统误差、半系统误差、不定常差等[2]),不易统一 一致的主要原因,即便是共性强的随机误差其量化指标也不一致(如标准差、平均误差、四分位差、中位绝对差等[2])。
因此,应强调统一规范化定量评定指标与估计方法,而非免用误差分类。如前已述,GUM 中只规范化了不确定度的评定方法,至于显著性的系统误差仍有待进一步规范化其评定指标和估计及修正方法,这仍然需要依据传统误差理论及其在系统误差评定上成熟经验。
4 测量不确定度评定与概率分布
GUM中强调指出,对不确定度的A类评定和B类评定分别按基于频率、基于信任度的概率分布所估计标准差来定量表示。这点与误差理论完全吻合,只不过其适用范围还未能满足当前误差理论发展要求,如对于测量模型输入分量的概率分布未能适用于不对称分布,其合成后输出量的概率分布还仅适用于近似正态分布或t分布等,以及测量模型的非线性度较严重等情况。尽管当前已补充了《用蒙特卡洛法评定测量不确定度》标准,却仍感不足,尤其在常见小样本数据处理中很难确定不确定度应基于那一个典型概率分布来定量表示。建议应用概率分布统示法[2~4],即统一采用一种模式分布密度函数p(x,θi),通过改变其参数i值来表示各种不同形态的具体分布pi(x),并要求表示出范围较广的各种常用对称分布和非对称分布,这样更加合乎实际情况。
因此,GUM 有待于进一步扩展应用于非正态分布和非对称分布,以及非线性测量模型等当前科技与误差理论发展现况的需要。
5 合成不确定度与误差合成理论
在GUM中按随机变量的方差传递规律导出不确定度传递律进行不确定度分量合成。这点也与误差理论中的误差合成理论基本符合。当测量模型y=f (x1, x2,…,xm)可线性化,即按Taylor级数展开可略去其二阶以上高阶项条件下,依据方差/协方差分量之和的合成方法,所得即为合成方差,也即可得合成标准不确定度:
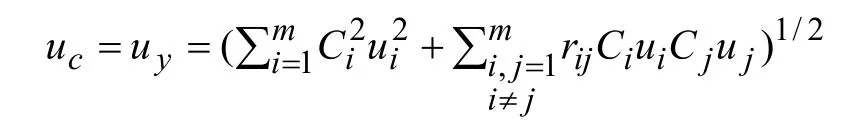
式中,uy为 y的标准不确定度;为函数y=f (x 1 , x2,…,xm)在与测量结果y对应的输入量值{}点处对xi的偏导数,即输入量xi单独对输出量y影响的线性化误差传递系数,也称为不确定度传递的灵敏系数;ui为输入量xi的标准不确定度;rij为xi与xj相关系数估计。这样的误差合成规律在传统误差理论中早已公认,只不过GUM再予以规范化而已。于是,在合成不确定度评定中,关键问题之一即确定灵敏系数Ci,估计相关系数rij及对相关项的处理方法等,均需借鉴以往误差合成方面的经验。
不仅如此,在扩展不确定度评定即U = kuc及确定包含因子k方面,就更离不开误差合成与极限误差估计方面的经验以及当今误差理论发展。实际上表述测量结果y的扩展不确定度 U目的,就是以很大的概率表示出被测量的真实值所在范围±U,显然将涉及误差合成概率分布这个难题。
在GUM中对扩展不确定度评定近作了简要的规定,如包含因子k一般取2或3,或者依据合成标准不确定度uc的有效自由度νeff而按t分布取kp= tp(νeff),p = 0.90~0.99。显然仅当合成概率分布接近于正态分布或t分布时可应用。实践以及用蒙特卡洛法仿真合成概率分布的结果[2,5]均已表明现有 GUM 的适用范围偏小了些,因此又补充了《用蒙特卡洛法评定测量不确定度》的标准。看来至少还应补充在非对称分布方面的应用。
由此可见,在测量不确定度评定上应用到误差理论的成果方面还远远不够。
6 关于GUM在扩展应用误差理论上的看法
误差理论随着科技的飞跃发展而不断地发展,显然测量不确定度评定技术也应随之有所进展,这点在GUM 中已有所注明。诸如:表明了只是评定和表示不确定度的通用规则,而不是详细技术规范和说明;未涉及专门测量领域的特殊问题,或不确定度定量表示的各种用途;只提供了评定不确定度的框架,并不能替代周密的思考、诚实的理智和专业的技巧;对不确定度的A类评定并未谈完,还有许多复杂的情况需用统计方法处理;对不确定度的B类评定也只是提示性的讨论等等。同时,在某些相应的条文中也提及应用最大熵方法、Bayes方法等一些非传统方法[1]。
显然,对于GUM也存在应适应于当前科技发展需要,及对测量可靠性和准确度有更高的要求形式,用于扩展应用问题。作者据当今误差理论发展的现况,提出以下若干应予扩展应用方面的意见供参考[2]。
——从传统正态分布误差扩展至非正态分布误差,尤其是非对称分布误差的分析与统计处理。实践表明非正态误差是客观存在的,因而近年来广泛开展对非正态误差各种概率分布形式描述、评定指标、估算及合成等各方面探讨,尤其对利用高阶矩或累积量(cumulant)分析方法与概率分布的级数展开法、统示法的研究。
——在传统最小二乘法基础上扩展至各种最小距离准则的处理方法。为适应各种不同专业领域技术要求、不同数据统计特性条件等,需要扩展至其它最小范数或最小距离准则下处理方法,如残差绝对值和为最小的最小一乘法、残差最大值为最小的最小∝乘法、以及其他的最小距离法等。还为了适应各种不同应用场合,而发展其处理方法,如采用正交变换、特征值或奇异值分解等算法、各种形式加权处理等,以及非线性模型处理方法等。
——从传统的最佳统计处理扩展至稳健统计(robust statistic)处理。因为实际数据常难满足独立性、正态性、无异常外部干扰或称“污染”等最佳性假定条件,而偏离这些条件,所采用的最佳估计或拟合方法将失去其最佳性,甚至会失效。而稳健估计和拟合方法可在数据稍有偏离原假定的概率分布模式,及受少量粗大误差或一些异常小误差污染下,仅使其估计或拟合结果作较小改变,其他仍基本上保持原有最佳性而不致失效,故稳健统计已成为现代数据处理中颇具活力的分支[2,6]。
——从传统统计处理方法扩展至Bayes统计处理方法。不仅只依靠现有数据作统计处理,而是再充分利用已有知识、经验、资料等先验信息,一起进行Bayes统计处理,以得出更为准确、可靠的结果,不确定度B类评定方法就考虑到应用这一统计原理[2]。
——从概率统计分析方法扩展到熵分析及熵优化分析方法。依据熵可作为信息不确定的唯一性度量,熵最大就意味着最大不确定性,以及每种随机变量概率分布都对应着一个熵值(逆转对应并不成立)等原理,即可用误差熵值反映其离散度,形成熵分析方法。又为避免求解具有多种可能解的各种不适定问题,只依据所得的数据含有的全部信息,而不再作任何主观假定,即在最不确定性即最大熵准则下求出不适定问题的解,简称最大熵方法。进而,在依据数据及所要求的约束条件上,又有已知的知识、经验、资料等可靠先验信息可用时,为使两种信息最大限度地相符合,即相互间的不确定性应最小,而按最小互熵准则来解题,简称最小互熵方法。于是可统归为熵分析与熵优化方法,这种方法的特点在于可不涉及概率分布的主观假定[2,7]。
——从静态测量数据处理扩展到动态测量数据处理。基于随机变量统计方法静态测量数据处理在变量动态测量广泛应用下已不尽适用,需扩展至基于随机过程的统计方法。尤其是长过程测量,包括变量测量过程和常量重复测量过程(如在线测量或质量控制中的长期监测等),为适应其未知复杂变化规律,及跟踪分析、处理和显示其时变统计特性(即特性量、技术参数或评定指标等),出现了各种自适应统计处理方法,包括各种递推式算法(recursive algorithm),以及近年来兴起的着重于精确描述上的移动式算法(moving algorithm)[2,8]。
还需特别指出,在计算机及其各种算法软件广泛应用与普及后,为了分析和解决误差分析及数据处理中的各种难题及开发新技术,又扩展应用了非统计方法。如计算机数值模拟或仿真分析方法;具有多分辨和变尺度的小波分析方法;模拟生物生存、进化、遗传等仿生分析方法;智能化分析方法等等。
总之,上述种种扩展应用均为GUM所未予涵盖,又是当前误差理论及数据处理中一直不断开发应用的技术。
可见,GUM实施实质上是对测量误差的一种(被测量值的分散性)定量表示起到规范化作用,今后对GUM 进行修订、补充、及拓展等显然仍应基于误差理论。
[1] 刘智敏,刘增明译.测量不确定度表示指南[J].BIPM-IECIFCC-ISO-IUPAC-IUPAP-OIML,《标准化文摘》增刊,1995,43.
[2] 林洪桦.测量误差与不确定度评估[M].北京:机械工业出版社,2010.
[3] 林洪桦.再荐误差的分布统示法[J].中国计量学院学报,2004,2:96-101.
[4] 林洪桦,潘锋.重复测量数据 β分布的自助法估计[J].北京理工大学学报,2004,11:947-951.
[5] 林洪桦,马升.误差分布及其合成分布判别的数值仿真分析[C],全国计量测试学术大会论文集,计量学报期刊社,1998.
[6] 林洪桦,席秀英.常量测试数据稳健性自动处理[J].全国现代误差理论及应用学术交流研讨会论文集,宇航计测技术,1997,增刊,48-54.
[7] 林洪桦,测量不确定度评定的熵方法[J].全国现代误差理论及应用学术交流研讨会论文集,宇航计测技术,1997,增刊,20-27.
[8] 林洪桦,动态测试数据处理[M].北京理工大学出版社.1995.

