一种变步长和变阶计算的自适应数值积分算法

杨录峰,马 宁,赵双锁,3

(1.北方民族大学信息与计算科学学院,宁夏银川 750021;2.吴忠市气象局,宁夏吴忠 751300;3.兰州大学数学与统计学院,甘肃兰州 730001)

一种变步长和变阶计算的自适应数值积分算法

杨录峰1,马 宁2,赵双锁1,3

(1.北方民族大学信息与计算科学学院,宁夏银川 750021;2.吴忠市气象局,宁夏吴忠 751300;3.兰州大学数学与统计学院,甘肃兰州 730001)

将自适应 Simpson算法和 Romberg外推算法相结合,提出一种新型的自适应 S-R(S impson-Romberg)算法,它兼有变步长计算和逐步提高数值积分法收敛阶的优点.若干数值比较算例表明,当被积函数在积分区间上变化性态急剧多变时,与自适应 Simpson算法和 Romberg外推算法相比,它具有明显优势.

数值积分法;自适应 Simpson算法;Romberg外推算法;自适应 S-R算法

数值积分

以自适应 Simpson算法[1-3]为优秀代表的一类自适应算法的主要优点是能根据 f(x)在积分区间[a,b]内变化的不同性态自动选择积分步长,因而在区间[a,b]上,该算法是变步长计算的.但这种算法在[a,b]上始终采用同一求积公式,故收敛阶是固定不变的,不管 f(x)多么光滑也是如此.数值积分(1)的另一类数值方法是外推算法,它在积分过程中可以不断使用由Richardson外推技术[4-5]得到的收敛阶更高的数值积分公式,只要 f(x)满足外推公式要求的光滑性条件和端点条件且控制条件许可,充分利用f(x)的光滑性利用Richardson外推过程以尽可能提高收敛阶,从而加快收敛速度,是这一类方法的优点[6].但这一算法在[a,b]上却是等步长的,它不能根据 f(x)在[a,b]上不同子区间的不同变化性态,选取最合理的变积分步长,除非事先把[a,b]划分成若干个小区间,然后分别求其数值积分,最后求它们的和.然而对[a,b]事先完成这一剖分却是困难的,因此,当被积函数 fx在[a,b]上变化性态是急剧多变时,该算法的有效性将受到限制,这一算法的优秀代表是由梯形公式不断外推的 Romberg算法[4].利用 Romberg求解数值积分的思想,MladenMestrovic与 Eva Ocvirk[7]将 Romberg算法应用于第 2类Volterra积分方程的数值求解问题.其他类数值积分方法,如蒙特卡洛方法[8],基于有限元的积分方法[9]等均有较快的发展.

本文将自适应 Simpson算法和 Romberg外推算法相结合构造了一种新型自适应算法,称之为自适应S-R(Simpson-Romberg)算法.该算法既能根据 f(x)在[a,b]上变化性态的多变性,对[a,b]自动剖分,又能充分利用 f(x)在[a,b]上的光滑性以尽可能提高收敛阶.可见,S-R算法兼有变步长计算和逐步提高数值积分收敛阶的优点,因而更具有有效性.对于变化性态改变不大的被积函数 f(x)的数值积分,数值算例表明该算法与 Romberg算法同样有效.

1 自适应 S-R算法

1.1 算法梗概

首先,在“低精度”ε1的控制下,用自适应 Simpson算法完成对积分区间[a,b]的剖分,使得 f(x)在剖分后所得到的每个小区间内每一点上的变化性态是相近的;然后在控制精度ε的要求下,利用Romberg外推算法完成每个小区间上的积分;最后把每一个小区间上所得到的数值结果求和,便得到 (1)的高精度近似积分结果.

1.2 若干术语

记 a ＜ b,α ＜γ,a≤α,γ≤b,h=γ-α,xj=α+jh/4,j=0∶4,β =x2

其中 Pαγ和 Qαγ分别是对 Iαγ近似积分的 3点和 5点 Simpson公式[6].所谓在 [α,γ]上做 Simpson试验 ,就是指分别算出 Pαγ和 Qαγ并对作判断.

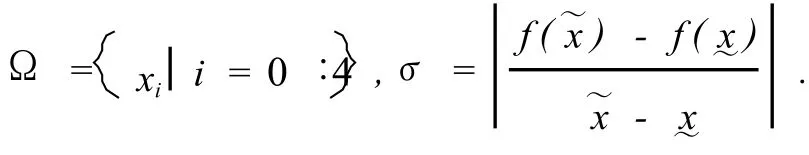
易知,当γ -α→0时,如记γ→ x＊,则σ → f′(x＊),故当γ-α足够小时,σ的大小在一定程度上反映了 f(x)在[α,γ]上每一点的变化激烈 (程)度,σ愈大,变化愈激烈,反之愈平缓.据此可以认为,当γ-α足够小时,σ为函数 f(x)在区间[α,γ]上每一点的变化激烈度的一个近似描述.

选取“低精度 ”ε0,定义

这里ε0是根据对 I近似积分的精度要求选取的.一般说来,若精度要求较低,则取ε0较大,反之较小,通常取ε0∈[10-1,10-2].考虑到,对 I近似积分精度要求实现的好坏,是与 f(x)的变化性态有关的事实,在本文中我们规定,当σ ＜10时取ε0=10-1,而当σ≥10时则取ε0=10-2,由程序自动完成.

为说明如何用自适应 Simpson算法对区间[a,b]实现剖分,先设在某个子区间 [α,γ]上用 Pαγ和 Qαγ近似计算 Iαγ.根据复合 Simpson公式的误差有:

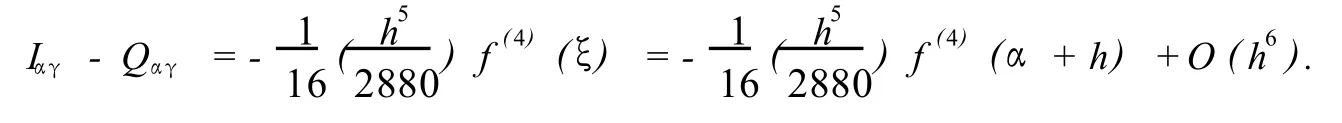
其中ξ,η∈[α,γ],两式相减,略去高阶项 O(h6)整理得

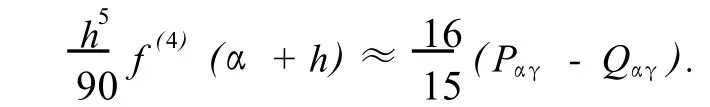
故

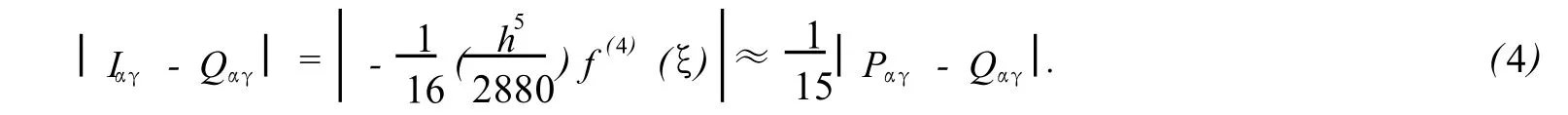
根据文献[6],如果要求

则可常使

由 (4),(5)和 (6)知,当α确定后,要求 (5)成立,实际上是确定γ =α+h使 (5)成立 (参见 1.3).故有下述定义:如果不等式 (5)成立,则称在子区间 [α,γ]上以精度为ε1的 Simpson试验,简称 Simpson试验是成功的,否则称为是失败的;如果是前者,我们还称 [α,γ]是实现 Romberg算法的一个区间,简称为 Romberg区间,有理由认为 f(x)在该区间上每一点的变化激烈度是相近的 (当然,所谓‘相近’是与ε0和相应的σ有关的).易知,在 f(x)的变化激烈度相近的区间上,Romberg算法是较为有效的.现设已经对区间[a,b]完成所有的 Simpson试验,即实现了对积分区间[a,b]的剖分 (剖分过程详见 1.3),得到 N个Romberg区间 [ti,ti+1],ti＜ ti+1,i=0:N-1,t0=a,tN=b.易知,诸 ti+1-ti一般并不相等;ε0愈小,诸ti+1-ti亦愈小;而且当σ ＞1愈大时,相应的 ti+1-ti愈小,记 Ii是 f(x)在 [ti,ti+1]上的积分,此处,Si是用 Romberg算法近似计算 Ii所得到的数值积分,满足

显然有

如果γ-α =(b-a)/2k,则称 [α,γ]是 [a,b]的一个 k级子区间,简称为 k级子区间;显然,[α,β]是[a,b]的 k+1级子区间,又称 [α,β]和 [β,γ]依次是 [α,γ]上的左 k+1级子区间和右 k+1级子区间,简称 [α,γ]上的左、右 k+1级子区间.

1.3 算法

1)令α =a,γ =b则γ-α =b-a,称 [α,γ]是 [a,b]的 0级子区间,简称为 0级子区间.如果 [α,γ]上 Simpson试验成功,则 [α,γ]就是 Romberg区间,否则转 2),

2)将 [a,b]分成 2个区间 [α,β]和 [β,γ],β -α =γ -β =(b-a)/2,则 [α,β]和 [β,γ]依次是 0级子区间 [a,b]的左、右 2个一级子区间.一般而言,设 [α,γ]是 [a,b]的 k级子区间 (它是 [a,b]的 k-1级子区间 (记为 [α,δ])的左 k级子区间,此处δ=α+(b-a)/2(k-1)),并设 [α,γ]上的 Simpson试验是失败的.现按“先左后右”的原则,在 [α,γ]上的左、右 2个 k+1级子区间 [α,β]和 [β,γ]上做 Simpson试验,共有 3种可能:

(i)如果分别在 [α,β]和 [β,γ]上的 Simpson试验均成功,则依次得到 2个 Romberg区间 [α,β]和[β,γ];下一步转向 k-1级子区间 [α,δ]上的右 k级子区间 [γ,δ]上的 Simpson试验,此处δ-γ =γ-α =(b-a)/2k.

(ii) 如果 [α,β]上的 Simpson试验成功 ,但在 [β,γ]上的试验失败 ,则 [α,β]是 Romberg区间 ,[β,γ]不是;下一步需做 [β,γ]上的 2个 k+2级子区间 [β,ξ]和 [ξ,γ]的 Simpson试验 ,这里ξ =(β +γ)/2.

(iii)如果 [α,β]上的 Simpson试验失败,则下一步要考察 [α,β]上的 2个 k+2级子区间 [α,η]和[η,β]的 Simpson试验,这里η =(α +β)/2.

现设[a,b]上的 Simpson试验已全部完成,这表明已用自适应 Simpson算法对区间[a,b]完成了剖分.可以看出,不管 f(x)在[a,b]上的变化性态如何,这种剖分总可完成.

3)从左至右,对每个Romberg子区间均按用户要求的控制精度ε使用Romberg算法,并完成所有子区间上的 Romberg结果求和,即得到 (1)的近似积分.

实际计算时,只要得到 1个 Romberg区间 (一定是从左到右依次得到的),就在该子区间上使用 Romberg算法已得到该子区间上的满足控制精度ε的 Romberg积分近似值,并与前面得到的近似结果累加,所得到的结果即为 (1)式的积分值.

说明在计算过程中,凡在 Simpson试验中所计算出的函数值均需要存储,在Romberg计算过程中需要时不再重新计算.

2 数值实验

下面所述的自适应 S-R外推算法相对于某一算法L的节省率μ(简称为节省率)是指:(算法L的函数计值个数 -自适应 S-R算法的函数计值个数)/自适应 S-R外推算法的函数计值个数.把“函数计值个数”简记为 f数,并记 H为最大积分步长,h为最小积分步长.

例 1计算积分[6]

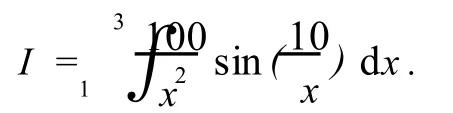
分别取ε =1.0×10-4,ε =1.0×10-7(精确解为:I=-1.426 024 756 346 27).利用自适应 Simpson算法、Romberg外推算法与自适应 S-R算法分别计算积分,计算结果见表1,Romberg区间端点分布 (计算函数点每隔 3点取 1点)见图 1.

表1 在 2种控制精度下的计算结果

例 2计算积分

控制精度为 =1.0×10 , =1.0×10 精确解为:I=29.326 213 804 391 15.分别利用自适应Simpson算法、Romberg算法与自适应 S-R算法计算积分,计算结果如表2,计算函数点的Romberg区间端点分布见图2.

表2 在 2种控制精度下的计算结果

例 3计算积分,控制精度分别为ε=1.0×10-5,ε=1.0×10-8(I＊=0.959 572 318 005)分别利用自适应 Simpson算法、Romberg算法与自适应 S-R算法计算积分,计算结果见表3.

表3 在 2种控制精度下的计算结果

3 结论

大量数值实验表明,针对数值求积,本文构造的既能变步长计算又能逐步分段提高收敛阶的自适应S-R算法,与自适应 Simpson算法和 Romberg外推算法相比较,当被积函数在积分区间上变化性态急剧多变时,具有明显的效率优势,而且,变化性态愈急剧多变,效率优势愈明显,而在相反的情形,其效率也不低于Romberg外推算法.而且可以看出积分精度要求愈高,节省率愈高或可以获得更高的精度.

[1]LYNESS J N.Notes on the adaptive Simpson quad-rature routine[J].J Assoc Comput,1969,16:83-495.

[2]GANDER W,GAUTSCH IW.Adaptive quadrature-revisited[J].BitNumericalMathematics,2000,40(1):84-101.

[3]ESPEL ID TO.Doubly adaptive quadrature routines based on Newton-Cotes rules[J].BitNumericalMathematics,2003,43(2):319-337.

[4]JOYCE D C.Survey of extrapolation processes in numerical analysis[J].S IAM Review,1971,13(4):435-490.

[5]杨录峰,金云超.一类含奇点函数的数值积分方法[J].云南民族大学学报:自然科学版,2010,19(1):16-19.

[6]R ICHARD L,BURDEN J.DOUGLAS F.Numerical analysis[M].7th ed.北京:高等教育出版社,2001.

[7]MESTROV ICM,OCV I RK E.An application of Romberg extrapolation on quadrature method for solving linearVolterra integral equations of the second kind[J].AppliedMathematics and Computation,2007,194(2):389-393.

[8]刘长虹,关永亮,寿卓佳,等.蒙特卡洛法在数值积分上的应用[J].上海工程技术大学学报,2010,24(1):43-46.

[9]石东洋,石东伟.一个非常规高效的数值积分方法[J].河南师范大学学报:自然科学版,2008,36(1):6-8.

(责任编辑万志琼)

An Adaptive Numerical Quadrature Algorithem of Comput ing with Both Changeable Step and Changeable Order

YANG Lu-feng1,MA Ning2,ZHAO Shuang-suo1,3
(1.Institute of Info rmation and Computation Science,BeifangUniversity ofNationalties,Yinchan 750021,China;2.WuzhongMeteorologicalBureau,Wuzhong 751300,China;3.Institute ofMathematics and Statistics,Lanzhou University,Lanzhou 730001,China)

Adaptive S-R(s impson-romberg)Algorithm,a new type of adaptive numerical quadrature algorithm,is presented,which combines the adaptive S impson algorithm with Romberg extrapolation algorithm.It possesses both the merits of the step-changeable computation and those of the gradual convergence order of numerical quadrature.The comparison of several numerical examples has indicated that the adaptive S-R algorithm has obvious superiority compared with the adaptive Simpson algorithm and the Romberg extrapolation algorithm when the integrand has some irregular property on the integration interval and the variation property over the interval of integration changes significantly.

numerical integration;adaptive simpson algorithm;romberg extrapolation algorithm;adaptive S-Ralgorithm

O 241.4

A

1672-8513(2011)01-0032-05

10.3969/j.issn.1672-8513.2011.01.008

2010-09-29.

国家自然科学基金(1096100);国家民委科研项目(09BF07);北方民族大学科研项目(2008Y032).

杨录峰 (1980-),男,硕士,助教.主要研究方向:数值计算、计算流体力学.