基于非线性浅水模型的铝电解磁流体动力学计算
徐宇杰, 李 劼, 张红亮, 赖延清
(中南大学 冶金科学与工程学院,长沙 410083)
基于非线性浅水模型的铝电解磁流体动力学计算
徐宇杰, 李 劼, 张红亮, 赖延清
(中南大学 冶金科学与工程学院,长沙 410083)
基于铝电解槽内流体体系及电磁场分布特点,建立了非线性磁流体动力学浅水模型,并应用此模型对某300 kA电解槽的熔体流场及铝液−电解质界面波动进行瞬态数值研究。在此基础上,通过动力学计算分析极距及铝液区垂直磁场对磁流体稳定性的影响。结果表明:随着极距的减小,界面波动由稳定趋向于不稳定;减小铝液区的垂直磁感应强度能大幅提高磁流体的稳定性。
铝电解;磁流体动力学模型;稳定性;数值计算
大型工业铝电解槽内的磁流体运动与电解生产的稳定性及关键技术指标息息相关,解析和优化槽内熔体运动一直是降低电解能耗、提高生产稳定性所遇到的核心难题之一。
国际上,铝电解磁流体运动数值研究始于20世纪70年代,至今已开展了30余年,其研究趋势总体上由稳态研究向瞬态研究发展。在瞬态研究方面,基于铝电解槽内电解质层或铝液层厚度与电解槽水平尺寸的比值为小参量的事实,URATA等[1−2]于20世纪80年代首先提出了浅水线性稳定性计算模型,该模型由一个波动方程和扰动电势方程组成,其实质只是分析由铝液−电解质界面波动引起的扰动电磁力对磁流体稳定性的影响,并未考虑熔体流动等对稳定性的影响;继URATA之后,DAVIDSON和LINDSAY[3−4],BOJAREVICS和ROMERIO[5]等也应用二维线性模型进行了相应的研究,除对稳定性判据进行探讨外,也给出了各自的稳定性方程组,这些方程组与URATA给出的基本一致;在此基础上,BOJAREVICS等[6−7]首先将熔体水平流动等因素耦合到稳定性方程,提出了基于浅水近似的非线性BOUSSINESQ方程组,随后又将非线性摩擦阻力引入模型,并将实际电磁场分布应用于耦合计算,然而BOJAREVICS推导非线性方程组时是基于两个小参量,除了认定槽内熔体层厚度与槽水平尺寸之比为小参量外,作者认为铝液的垂向波动量与极距之比也为小参量,这与实际情况不甚相符;同时,ZIKANOV等[8−10]应用Shallow water方程组、de St. Venant方程组进行了非线性研究,模型引入了线性摩擦阻力,并重点分析了铝液、电解质流场对稳定性的影响,然而,ZIKANOV的模型未耦合实际计算所得的电磁场结果,也完全忽略了流动粘性力项,在完整描述熔体流动行为方面有所欠缺。由上可见,首先,铝电解磁流体瞬态研究普遍采用二维浅水模型,其原因在于采用三维模型进行瞬态研究,计算量过于巨大,需耗费大量资源,同时槽内流体体系属典型的浅水体系,采用二维模型是对研究对象的有效近似;其次,铝电解磁流体瞬态数值研究经历了从线性到非线性的发展过程,从单因素的界面波动计算逐步转为多物理量耦合的瞬态计算,研究模型实质上已由传统的稳定性模型发展为磁流体动力学模型,但是模型尚未完善,尤其是需妥善处理流体体系的合理简化与流动行为的精确描述这两者之间的关系。国内在该领域的研究与国外有较大差距,在非线性模型研究方面,尚无相关文献报道。
本文作者建立非线性浅水模型,耦合全槽三维仿真获得的电磁场分布,对铝电解磁流体运动进行动力学分析,为大型铝电解槽的设计及优化提供有效的方法和依据。另外,关于极距及磁场对磁流体稳定性的影响,前人已根据工业实践和线性模型分析得出了基本的结论[11−12],本文作者将应用非线性模型对此作进一步的论证。
1 理论模型
1.1 浅水模型及控制方程
大型工业铝电解槽是一长方体容器,其水平长度Lx和水平宽度Ly通常分别为15和4 m左右,其内铝液层厚度H和极距间电解质层厚度h分别为20和5 cm左右。因此,可作出以下假设:

式中:λ为界面波动的典型波长,与电解槽水平尺寸处同一数量级。
根据式(1),铝电解槽内流体体系符合浅水特征,可应用二维动力学模型对槽内熔体运动进行数值研究。忽略阳极气泡相,槽内为铝液、电解质分层两相流,本文提出如下浅水控制方程组:

式中:U、P和ρ分别为流速、热力学压强以及密度;t和g分别为时间和重力加速度;ζ为铝液−电解质界面垂直波动量(偏离初始位置的距离);上标“a”和“c”分别指铝液和电解质。在描述熔体流动所受的外摩擦阻力时,本研究采用线性模型,κ为摩擦因数。考虑到熔体运动内摩擦作用亦不可忽略,本控制方程中保留了粘性力项,νe为有效运动粘度,对铝电解槽内的熔体而言,其物理粘度远小于湍流粘度(相差2~3个数量级),故可用湍流粘度近似代替有效粘度,本研究采用常湍流粘度模型[13−14]。另外,需指出的是控制方程中相关物理量的值为其垂直方向上的均值,如铝液流速Ua可由式(6)描述:

式中:ua为槽内实际铝液流速。
本模型只需要流速边界条件,设定槽周为光滑无渗透壁面,即:

式中:n为边界外法线方向。
对于本动力学模型的机理可作如下描述:上层电解质和下层铝液在电磁力(非扰动部分)的驱动下作湍流流动,导致流体内部压强改变,使得铝液−电解质界面发生变形,槽内电磁场分布相应改变,产生额外的电磁力(扰动部分),扰动电磁力进一步改变流体的流动并影响铝液−电解质界面的波动,在这个过程中可能产生波动的不稳定分量,如果无法有效抑制摩擦阻力,则波幅不断增大,即出现磁流体不稳定现象。
1.2 电磁力模型
电磁力是槽内熔体运动的主要驱动力,将铝液−电解质界面未变形前提下流体区域分布的电磁力定义为F0,将由界面变形引起的作用于流体的电磁力定义为f,则某一时刻铝液所受电磁力Fa和电解质所受电磁力cF可分别由式(8)和(9)表示:

1.2.1 非扰动电磁力

式中: J和B分别为电流密度和磁感应强度,“⊥”表示水平分量。本研究采用的电磁场分布由三维全槽仿真获得,电磁场的建模及计算参见文献[15]。
1.2.2 扰动电磁力

为计算扰动电磁力,先对槽内电磁特性进行讨论。铝液、电解质和阴极炭块的电导率(σ)满足如下关系:当铝液−电解质界面发生变形时,电解质层局部阻抗改变,产生扰动电流,扰动电流又诱发相应的扰动磁场。由于电解质的导电性差,电流尽可能以最短路径通过电解质层,因此该层中的扰动电流主要是垂直方向上的;由于铝液的导电性远优于电解质及阴极炭块的导电性,造成扰动电流在铝液层中封闭,因此铝液层中的扰动电流主要是水平方向上的。槽内扰动电流及扰动磁场分布如图1所示。
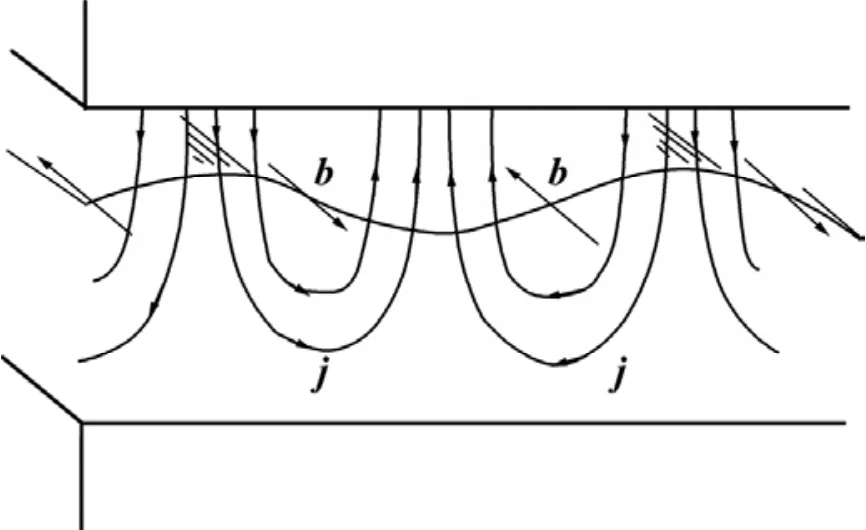
图1 槽内扰动电流及扰动磁场Fig.1 Current and magnetic perturbations in cell
在以上讨论的基础上,DAVIDSON和LINDSAY[3]及BOJAREVICS和ROMERIO[5]推导出铝液层水平电流与垂直磁场作用产生的电磁力是唯一有重要影响的扰动电磁力组分。
据此,可以得到以下结论:

式中:下标“z”表示电解槽高度方向。
由于电解质层中的电流基本上是垂直的,故可将铝液上表面视为等势面,并设定:

在此基础上得到阳极底面处的电势为

假设阳极底面处的电势相等,则可得:

根据上述扰动电流的特征,应用泊松方程计算铝液中的水平电流:
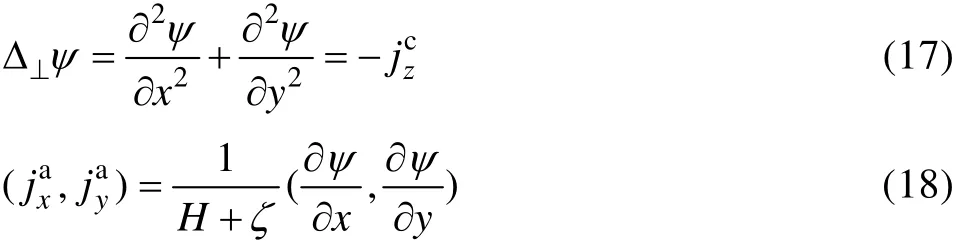
式中:ψ为电流势。扰动电流模型的边界条件为
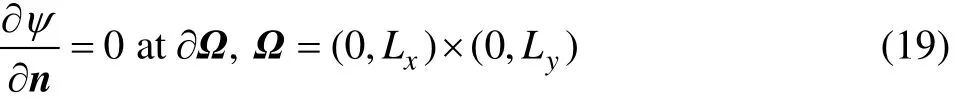
应用式(13)~(19),扰动电磁力可获得有效求解。
2 计算实例
根据以上建立的数学模型,应用有限元法对某300 kA电解槽进行磁流体动力学计算。该槽流体区域水平长度Lx和宽度Ly分别为14.56和3.56 m,极距h和铝水平H分别取5和22 cm,其他计算所用参数见表1。线性摩擦因数是模型中唯一没有确定的参数,其值显然与阴极、阳极及壁面的表面特性等相关,且应基于实测数据加以描述,但目前尚缺乏相关方面的研究。在本算例中,研究对象在上述技术指标下不会出现不稳定现象,熔体运动会由最初的非稳态逐渐趋于稳态,通过将不同摩擦因数下稳定后的结果与本槽三维稳态计算的结果对比,获得合适的摩擦因数值,如表1所示。
本算例电解槽内熔体在受到扰动后,流场能较快趋向稳定,铝液−电解质界面也由较大幅度的全局波动逐渐转为小幅局部波动,在1 000 s左右波动消失,稳定界面形成。图2和3所示分别为计算所得稳定后的铝液流场和电解质流场分布,其铝液的最大流速为0.226 m/s,平均流速为0.041 m/s,电解质的最大流速为0.139 m/s,平均流速为0.037 m/s。图4所示为稳定后的界面变形情况,沿着阳极方向的最大变形量为0.014 6 m。

表1 某300 kA槽磁流体动力学计算相关参数Table 1 Parameters used in MHD computation for 300 kA cell

图2 某300 kA槽稳定后的铝液流场Fig.2 Steady flow field of metal in 300 kA cell (t=1 050 s)
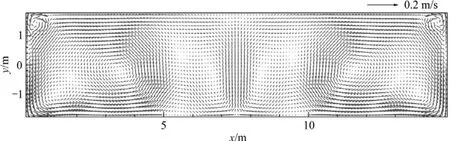
图3 某300 kA槽稳定后的电解质流场Fig.3 Steady flow field of bath in 300 kA cell (t=1 050 s)
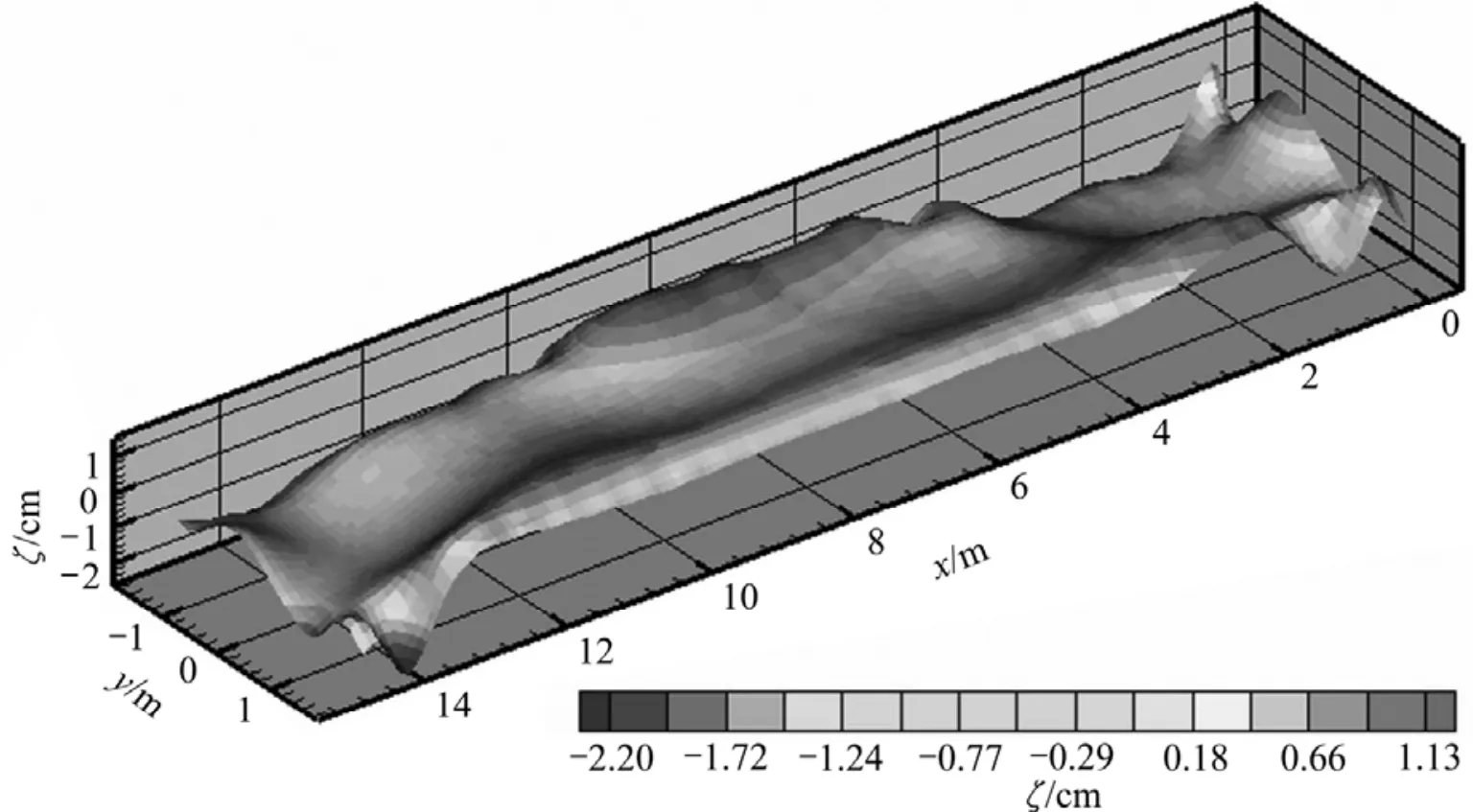
图4 某300 kA槽稳定后的铝液−电解质界面变形分布Fig.4 Steady metal-bath interface deviation in 300 kA cell (t=1 050 s)
3 极距对磁流体稳定性的影响
工业铝电解生产中,减小极距可大幅降低电解能耗,但极距的改变会影响槽内磁流体的稳定性。铝电解的磁流体稳定性主要是指铝液−电解质界面的波动是否随时间延长而消失。本研究仍以上述 300 kA槽为研究对象,应用非线性动力学模型对该槽在不同极距下运行的磁流体稳定性进行计算和分析。图5~8所示分别为计算所得极距为5.0、4.7、4.4和4.3 cm时的铝液−电解质界面波动曲线,图中横坐标为时间,纵坐标为ζmean/h,ζmean表征了界面的整体变形状况,其定义表达式如下:

式中:“〈〉”表示定义域内积分。
由图5~7可知,在前3个极距下磁流体都是稳定的,但可以看出随着极距值的减小,稳定的趋势随之减弱,达到稳定所需的时间明显增加,稳定后界面的相对变形程度增大。由图8可知,极距为4.3 cm时的铝液−电解质界面波动随时间不断放大,即出现了磁流体不稳定现象。图9和10所示分别为4.3 cm极距下516 和1 865 s时的铝液-电解质界面分布。由图9和10可知,界面变形量明显增大。综上所述,从磁流体稳定性角度出发,该槽的临界极距应为4.3~4.4 cm,在实际工业生产中,该电解槽的极距维持在4.5 cm左右。

图5 铝液−电解质界面波动曲线(300 kA, h=5.0 cm)Fig.5 Metal-bath interface wave curve(300 kA, h=5.0 cm)
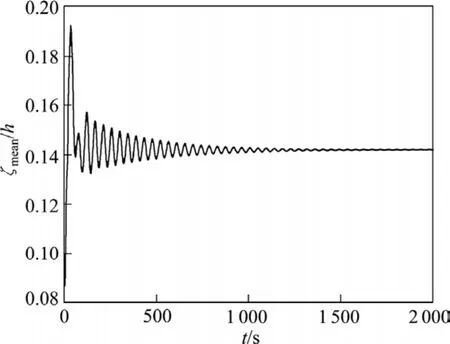
图6 铝液−电解质界面波动曲线(300 kA, h=4.7 cm)Fig.6 Metal-bath interface wave curve(300 kA, h=4.7 cm)
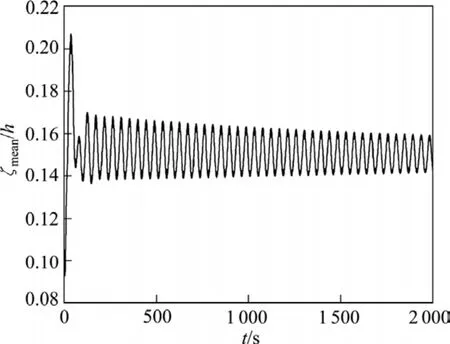
图7 铝液−电解质界面波动曲线(300 kA, h=4.4 cm)Fig.7 Metal-bath interface wave curve(300 kA, h=4.4 cm)
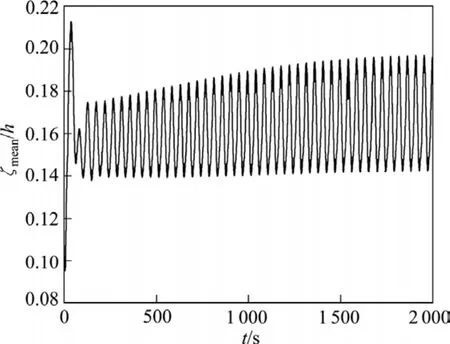
图8 铝液−电解质界面波动曲线(300 kA, h=4.3 cm)Fig.8 Metal-bath interface wave curve(300 kA, h=4.3 cm)

图9 铝液−电解质界面变形分布(300 kA, h=4.3 cm, t=516 s)Fig.9 Distribution of metal-bath interface deviation (300 kA, h=4.3 cm, t=516 s)
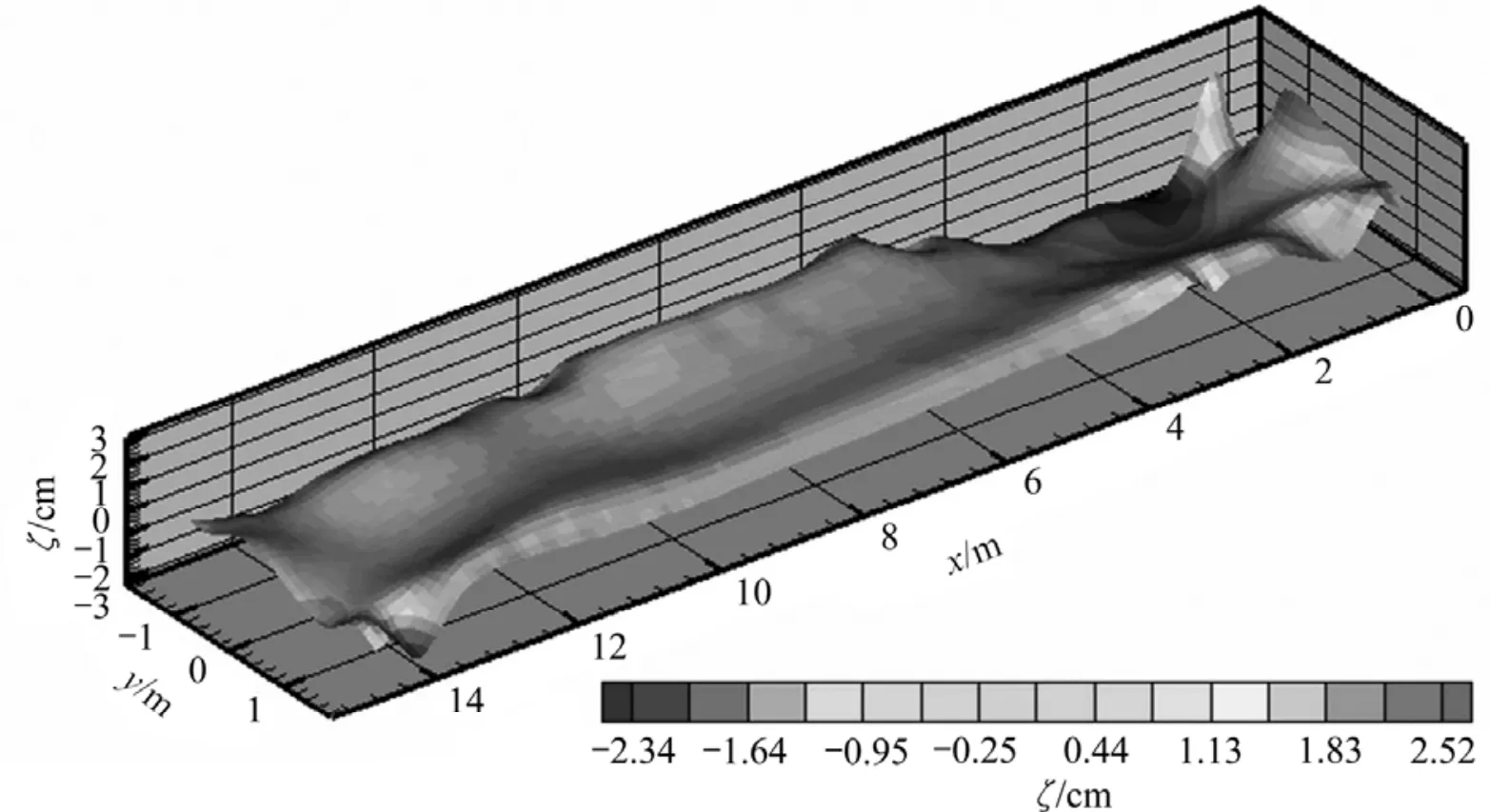
图10 铝液−电解质界面变形分布(300 kA, h=4.3 cm, t=1 865 s)Fig.10 Distribution of metal-bath interface deviation (300 kA, h=4.3 cm, t=1 865 s)
4 铝液中的垂直磁场对磁流体稳定性的影响
铝液中的垂直磁场是影响槽内磁流体稳定性的又一个重要因素,本研究应用非线性动力学模型对此进行研究。上述300 kA槽在极距为4.3 cm下呈现不稳定现象,在不改变极距的前提下,将其铝液层中的垂直磁感应强度改为实际分布值的90%和70%,再分别进行瞬态计算,获得的铝液−电解质界面波动曲线分别如图11和12所示。由计算结果可知,当铝液中的垂直磁感应强度改为实际分布值的90%时,磁流体即由不稳定转为稳定(在1 000 s左右波动基本消失),继续减小垂直磁场至70%时,界面波动现象进一步得到削弱(在400 s左右波动消失)。另外,两种情况下稳定后的最大界面变形量分别为1.73和2.22 cm。由此可证明,分布于铝液层的垂直磁场对磁流体稳定性有着十分突出的负面影响,减小垂直磁场可有效提高磁流体的稳定性。
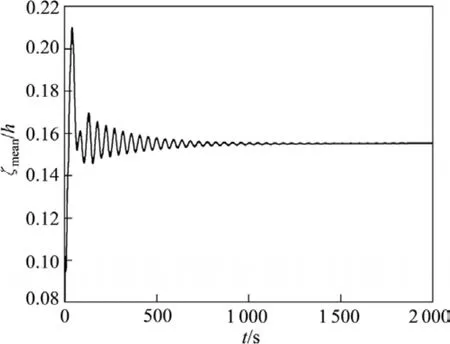
图11 铝液−电解质界面波动曲线Fig.11 Metal-bath interface wave curve (300 kA, h=4.3 cm, B=0.9B)
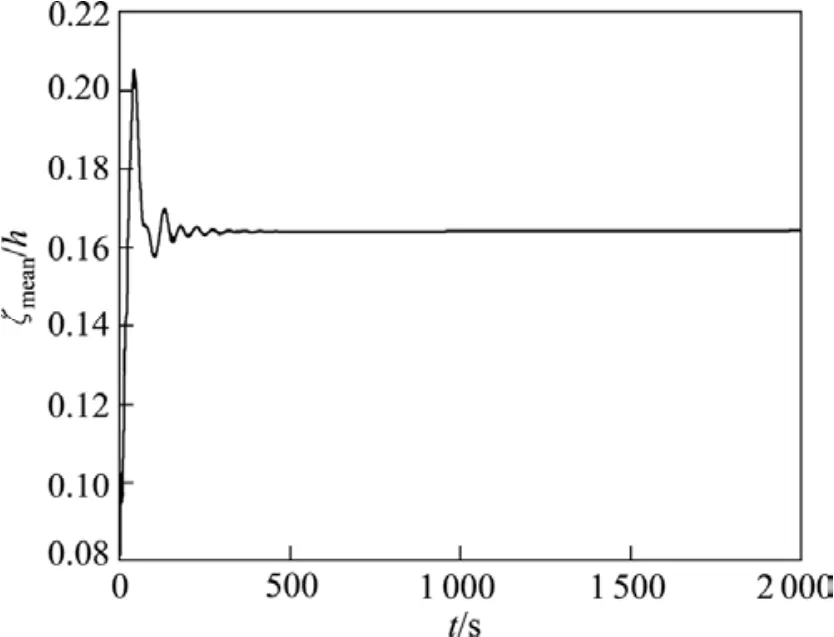
图12 铝液−电解质界面波动曲线Fig.12 Metal-bath interface wave curve (300 kA, h=4.3 cm, B=0.7B)
5 结论
1) 基于铝电解流体体系及电磁场分布特点,建立了非线性磁流体动力学浅水模型,实现了熔体流场及铝液−电解质界面波动的瞬态计算,在此基础上,应用此模型对某300 kA铝电解槽的磁流体运动进行了数值研究。
2) 减小极距将使槽内磁流体运动由稳定趋向不稳定,因此存在磁流体稳定性临界极距,本研究计算对象为某300 kA槽,其临界极距在4.3~4.4 cm之间。
3) 铝液层中的垂直磁场对槽内磁流体稳定性的影响显著,通过物理场优化设计减小分布于铝液层的垂直磁场是改善铝电解磁流体稳定性的重要途径。
REFERENCES
[1] MORI K, SHIOTA K, URATA N, IKEUCHI H. The surface of oscillation of liquid metal in aluminum reduction cells[C]//LEAVITT S R. Light Metals 1976. Las Vegas, NV: Metallurigical Society of AIME, 1976: 77−95.
[2] URATA N. Magnetics and metal pad instability[C]//BOHNER H O. Light Metals 1985. New York, NY: Metallurgical Society of AIME, 1985: 581−591.
[3] DAVIDSON P A, LINDSAY R I. A new model of interfacial waves in aluminum reduction cells[C]//HUGLEN R. Light Metals 1997. Orlando, FL: TMS, 1997: 437−442.
[4] LINDSAY R I, DAVIDSON P A. Stability of interfacial waves in aluminum reduction cell[J]. J Fluid Mech, 1998, 362: 327−331.
[5] BOJAREVICS V, ROMERIO M V. Long waves instability of liquid metal-electrolyte interface in aluminum electrolysis cells: A generalization of Sele's criteria[J]. European Journal of Mechanics B/fluids, 1994, 13: 33−56.
[6] BOJAREVICS V. Non-linear waves with electromagnetic interaction in aluminium electrolysis cells[J]. Progress in Fluid Flow Research: Turbulence and Applied MHD (AIAA), 1998, 58: 833−848.
[7] BOJAREVICS V, PERICLEOUS K. Comparison of MHD models for aluminium reduction cells[C]//GALLOWAY T J. Light Metals 2006. San Antonio, TX: TMS, 2006: 347−352.
[8] ZIKANOV O, THESS A, DAVIDSON P A, ZIEGLER D P. New approach to numerical simulation of melt flows and interface instability in Hall-Héroult cells[J]. Metallurgical and Materials Transactions B: Process Metallurgy and Materials Processing Science, 2000, 31(6): 1541−1550.
[9] SUN H, ZIKANOV O, ZIEGLER D P. Non-linear two-dimensional model of melt flows and interface instability in aluminum reduction cells[J]. Fluid Dynamics Research, 2004, 35(4): 255−274.
[10] SUN H J, ZIKANOV O, FINLAYSON B A, ZIEGLER D P. The influence of the basic flow and interface deformation on stability of Hall-Heroult cells[C]//KVANDE H. Light Metals 2005. Calgary, Alberta, Ca: TMS, 2005: 437−441.
[11] URATA N. Wave mode coupling and instability in the internal wave in aluminum reduction cells. [C]//Light Metals 2005. San Francisco, CA: TMS, 2005: 455−460.
[12] WU J K, HUANG M, HUANG J, YAO S H. Finite element analysis of magnetohydrodynamics stability of an aluminum reduction cell[C]//SCHNEIDER W. Light Metals 2002. Seattle, WA: TMS, 2002: 511−514.
[13] POTOCNIK V, LAROCHE F. Comparison of measured and calculated metal pad velocities for different prebake cell designs[C]//ANJIER J L. Light Metals 2001. New Orleans, LA: TMS, 2001: 419−425.
[14] SEVERO D S, SCHNEIDER A F, PINTO E C V, GUSBERTI V, POTOCNIK V. Modeling magnetohydrodynamics of aluminum electrolysis cells with ANSYS and CFX[C]//KVANDE H. Light Metals 2005. San Francisco, CA: TMS, 2005: 475−480.
[15] LI Jie, LIU Wei, LAI Yan-qing, LIU Ye-xiang. Improved finite element model for electro-magnetic analysis in aluminum cells[J]. JOM, 2008, 60(2): 58−61.
[16] SEVERO D S, GUSBERTI V, SCHNEIDER A F, PINTO E C V, POTOCNIK V. Comparison of various methods for modeling the metal-bath interface[C]//DEYOUNG D H. Light Metals 2008. New Orleans, LA: TMS, 2008: 413−418.
(编辑 何学锋)
MHD calculation for aluminium electrolysis based on nonlinear shallow water model
XU Yu-jie, LI Jie, ZHANG Hong-liang, LAI Yan-qing
(School of Metallurgical Science and Engineering, Central South University, Changsha 410083, China)
A nonlinear magnetohydrodynamic (MHD) shallow water model was established, based on the characteristic of both the fluid system and the distribution of electromagnetic field in cell. Using the model, a transient numerical study on the melts flow field and the metal-bath interface wave in a 300 kA cell was carried out. Furthermore, the influence of both anode-cathode distance (ACD) and vertical magnetic field in the metal on the MHD stability was analyzed by dynamic computation. The results show that the interface wave tends to be unstable from a stable state with ACD decreasing, and the MHD stability can be improved markedly by reducing the vertical magnetic flux density in the metal layer.
aluminium electrolysis; MHD model; stability; numerical computation
TF 821;O 441.4
A
1004-0609(2011)01-0191-07
国家高技术研究发展计划资助项目(2008AA030504);国家重点基础研究发展计划资助项目(2005CB623703);国家自然科学基金资助项目(50874120);
2010-01-07;
2010-05-27
张红亮,博士;电话:13574831278;E-mail:cau13574831278@163.com

