AZ31铸造镁合金的塑性流动特征及物理概念的本构关系

苏 静，郭伟国，何可馨，鬲钰焯

(西北工业大学 航空学院，西安 710072)

AZ31铸造镁合金的塑性流动特征及物理概念的本构关系

苏 静，郭伟国，何可馨，鬲钰焯

(西北工业大学 航空学院，西安 710072)

利用准静态试验机以及Hopkinson压杆装置对AZ31铸造镁合金在不同应变速率和不同温度下的塑性流动性能进行研究，结合金相显微技术对试验后的试样进行微观分析。结果表明：在低应变速率下，随着温度的升高，AZ31镁合金发生明显的由脆性到韧性的转化，其转化温度为473 K左右；当应变速率增加到1.2×104s−1时，会发生脆化现象，塑性变形能力变差。基于微观分析，低应变速率下晶体中孪晶的存在是促进材料塑性变形增加的主要因素。而在高应变速率下，动态再结晶和第二相粒子沉淀硬化显著地影响金属的塑性变形。结合系统的试验结果，基于热激活位错机制，建立一种物理概念的塑性流动本构模型，对较高应变速率和不同温度下的流动应力进行模型预测。通过对比，模型预测结果与试验数据吻合较好。

AZ31镁合金；塑性流动；应变速率；微观机理；本构关系

镁合金具有密度低(约1.8 g/cm3)、比强度高、弹性模量大、减震性好、承受冲击能力强、耐有机物和碱的腐蚀性能良好等特点，成为航空器、航天器和火箭导弹等制造工业中最有前途、最轻的金属结构材料[1−2]。

金属镁属于典型的hcp结构。以镁为主要成分的AZ31镁合金在室温下的塑性变形能力较差，在低应变速率下压缩破坏应变通常小于10%。目前，有关镁合金塑性以及超塑性研究很多。稀土元素的加入，热处理方式的改变均会影响镁合金的塑性[3]。从微观机理上分析，材料内部晶体结构的变化是影响其塑性变形的根本原因，晶粒内部的滑移、孪生以及晶界的移动都可影响镁合金的塑性变形能力[4−5]。在高应变速率下，材料的动态再结晶导致晶粒细化，也影响材料的塑性变形能力。晶粒细化是当今材料领域的一个研究热点。而在冲击载荷作用下，镁合金的高应变速率、大变形行为和相关规律的研究较少[6−7]。对镁合金本构关系的研究，多数是建立在低应变速率下不同温度的情况[8−10]，而对高应变速率下不同温度的情况研究较少[11]。

本文作者首先对铸造镁合金AZ31在应变速率从1.0×10−3到1.0×105s−1，温度从77到600 K左右的塑性流动应力—应变规律进行研究，利用金相显微镜对变形试样的微观结构进行观测，对变形机理进行分析；然后，基于热激活位错动力学，建立适应于较高应变速率、不同温度下的物理概念本构模型，对模型预测结果和试验结果进行比较和分析。

1 实验

试验所用材料为铸造镁合金AZ31，准静态实验及5.0×103s−1时试样尺寸为d 5 mm×5 mm，而1.2×104s−1时试样尺寸为d 2 mm×2 mm，试验材料的主要化学成分如表1所列。

应变速率为1.0×10−3～1.0×10−1s−1，温度为77～573 K下的低应变速率试验，采用CSS4410型电子万能材料试验机。试验过程中试样通过两根耐高温陶瓷棒加载，试样与陶瓷棒之间涂有三硫化二钼以减少端面摩擦。试样的变形通过试验机的位移传感器测试。试验前，采用引伸计对位移传感器进行比对标定。

对于应变速率为1.0×103～1.2×104s−1，温度为293～523 K的高应变速率试验，采用可进行高温高应变速率耦合的分离式Hopkinson压杆装置[11−12]。

为了对变形后的试样进行金相观察，将变形后的试样沿加载轴线方向切开，用硝酸−乙酸−草酸(硝酸1 mL，乙酸(99%) 1 mL，草酸1 g，蒸馏水150 mL)腐蚀液腐蚀15 s左右抛光，然后在金相显微镜下进行观察。

2 结果与分析

2.1 准静态试验结果与分析

AZ31镁合金在低应变速率、不同温度下的真应力—应变曲线如图1所示。随着温度的升高，塑性流动应力显著下降，表现为明显的温度负敏感性。从77到373 K，材料的变形较小，应变小于13%。而从473到573 K，随着温度的升高，材料软化程度增加，材料的塑性应变明显增加。图1(a)中，当应变速率为1.0×10−3s−1时，温度上升至573 K时，变形应变超过40%。图1(b)中，当应变速率为1.0×10−1s−1，温度上升至573 K时，最终破坏应变超过35%。从图1这可看出，473 K可以被认为是AZ31镁合金脆−韧转变的临界温度。

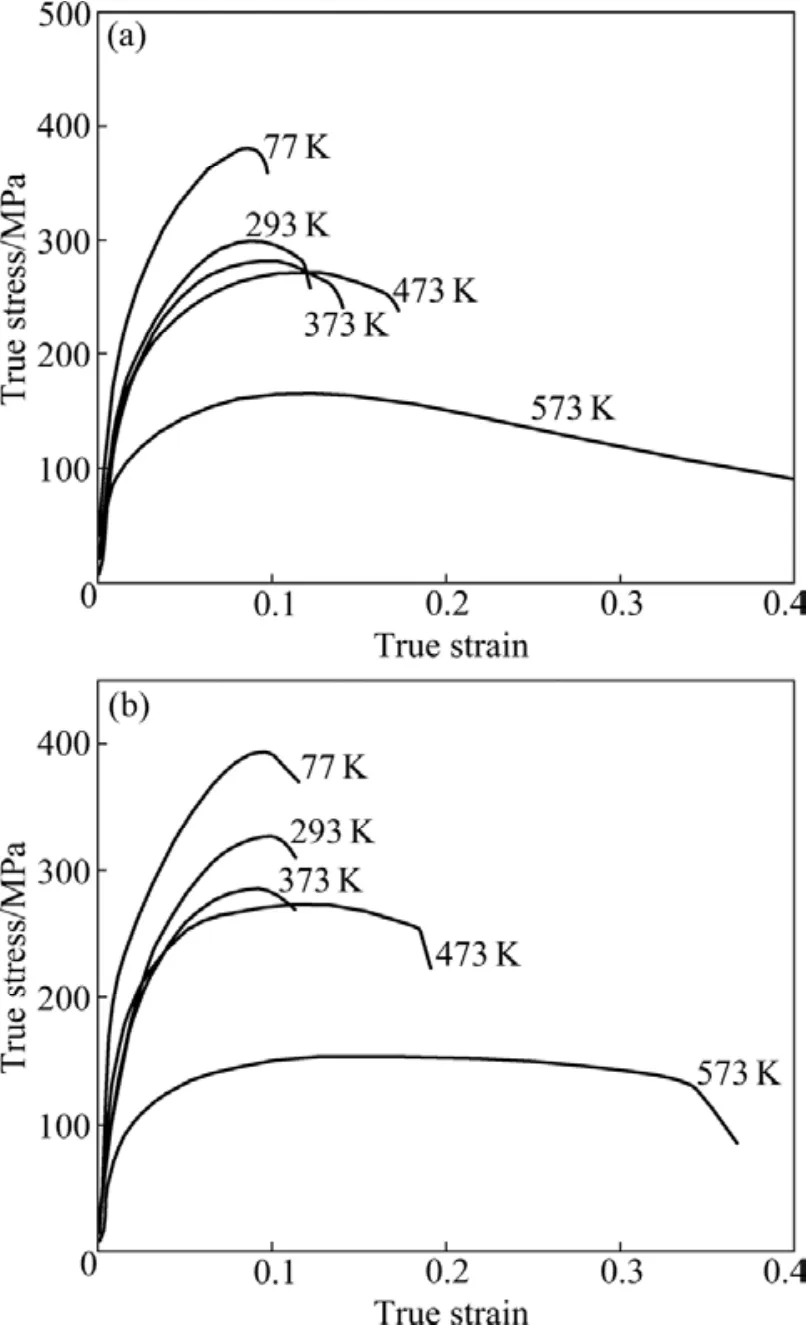
图1 AZ31镁合金在不同应变速率下的真应力—应变曲线Fig.1 True stress—strain curves of AZ31 magnesium alloy at different strain rates: (a) 1.0×10−3s−1; (b) 1.0×10−1s−1

2.2 动态试验结果分析

图2所示为高应变速率(5.0×103s−1)下AZ31镁合金典型的应力—应变曲线。由于在试验过程中控制试样的变形，图中曲线的最大应变点试样并没有破坏。在高应变速率下，流动应力呈现较平滑的应变硬化稳定区，此区也为应变硬化和应变软化相持恒的过程。与低应变速率情况(见图1)相比，在高应变速率下，流动应力上升，呈现应变速率敏感性。在1.2×104s−1的超高应变速率下(见图3)，试样均在最大应变点处破坏。此时AZ31镁合金的塑性变形能力只有约10%左右，温度升高到523 K，破坏应变只有8%。且随着温度的升高，流动应力出现下降。

图2 应变速率为5.0×103s−1时AZ31镁合金塑性流动应力—应变曲线Fig.2 True stress—strain curves of AZ31 magnesium alloy at strain rate of 5.0×103s−1

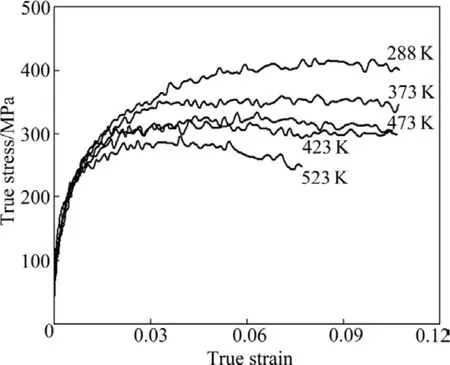
图3 应变速率为1.2×104s−1时AZ31镁合金塑性流动应力—应变曲线Fig.3 True stress—strain curves of AZ31 magnesium alloy at strain rate of 1.2×104s−1

图4和5分别为AZ31镁合金塑性流动应力与温度、塑性流动应力与应变速率的关系。从图4和5可以看出，AZ31镁合金具有较强的温度和应变速率敏感性。图4中，当温度由423 K升高到523 K时，流动应力出现随温度升高而增加的现象，此现象可能是动态应变时效现象[13]。

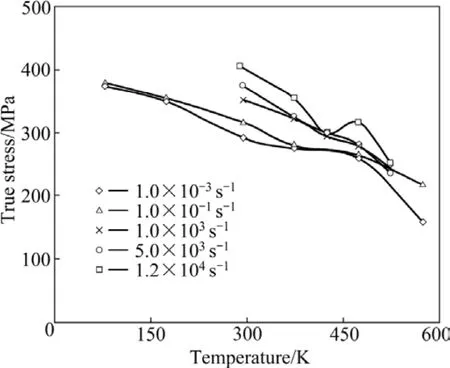
图4 应变为7.5%时AZ31镁合金在不同应变速率下的应力—温度曲线Fig.4 True stress—temperature curves of AZ31 magnesium alloy at strain of 7.5%

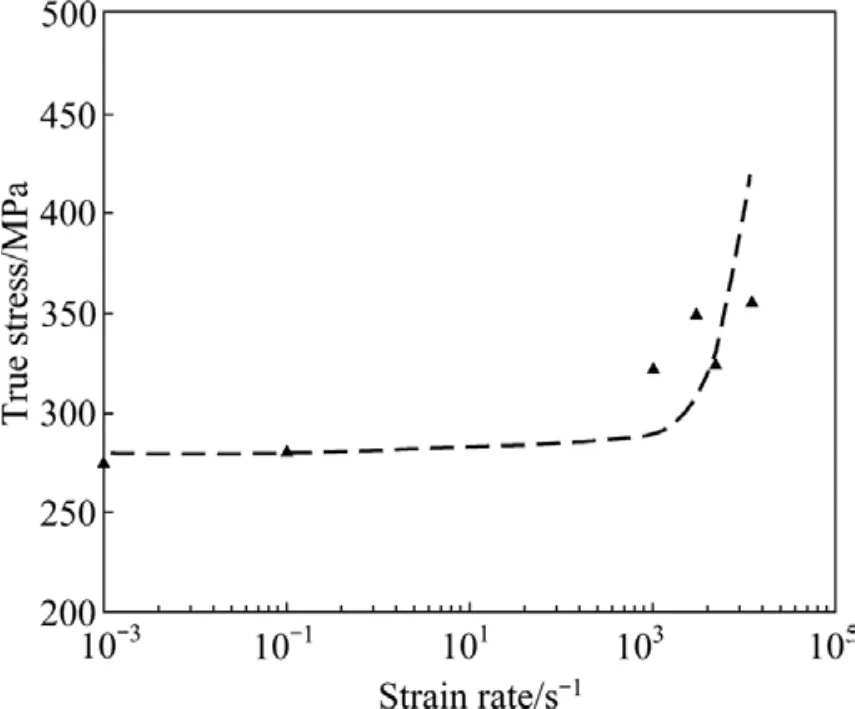
图5 应变为7.5%、温度为373 K时AZ31镁合金真应力—应变速率曲线Fig.5 True stress—strain rate curve of AZ31 magnesium alloy at initial temperature of 373 K and fixed true strain of 7.5%

由以上分析可知：1) 在低应变速率下，随着温度的升高，AZ31镁合金发生明显的由脆性到韧性的转化，其转化温度为473 K左右；2) 随着应变速率的升高，材料的塑性变形能力增强。而当应变速率增加至1.2×104s−1时，材料的塑性变形能力反而降低，出现脆化现象。

3 微观机理分析

金属塑性变形时滑移总是有利于沿着原子密排面和密排方向进行。镁是典型的密排六方(hcp)结构，它在塑性变形时常会发生基面{0001}〈120〉的滑移以及锥面{102}〈101〉的孪生。

与其他金属相比，镁晶体只有3个几何滑移系和2个独立滑移系。镁的滑移系较少是镁合金不易产生宏观屈服而容易在晶界处产生大量的应力集中、从而塑性变形能力差的主要原因。此外，由于变形时易沿孪晶区域或大晶粒的基面{0001}产生局部穿晶断裂，纯镁以及普通铸造镁合金具有脆化倾向。而纯镁的棱柱滑移面{100}〈110〉不活泼，只有在温度升高时才可以被激活，使得镁在高温下的塑性变形能力增强。

以密排六方(hcp)多晶体镁形成的铸造镁合金AZ31主要呈现hcp结构的特征。由图6可以看出：在低应变速率下，当温度由83升高到373 K时，晶体内部已经有大量的孪晶生成，此时，孪晶成为影响材料塑性变形的主要因素之一。孪生可以改变晶粒的取向，促进滑移的形成，并且可以释放局部应力集中，促进裂纹的形核。当温度升高到573 K时，晶体内部的孪晶开始减少。由图6(c)可以看出，部分晶界处已经出现大量的细小晶粒，即出现再结晶现象。这主要是由于原始晶界对位错运动具有阻碍作用，使得晶界附近的位错不断塞积，位错密度不断增大。当位错密度达到某一临界值时，再结晶晶粒优先在晶界处形核。同时，由于动态再结晶的软化作用，流动应力下降。

在高应变速率情况下，AZ31镁合金的微观结构如图7所示。由图7可以看出：在应变速率为1.0×103s−1、温度为523 K、应变为12%的条件下(见图7(a))，晶体内部的孪晶逐步消失，且动态再结晶引起晶粒细化，随着应变速率的增大，晶粒细化程度逐渐增强；而在应变速率为5.0×103s−1、温度为523 K、应变为16%的条件下(见图7(b))，晶粒的平均尺寸为3 μm左右，且细小晶粒分布均匀，动态再结晶的软化作用使得流动应力下降；在应变速率为1.2×104s−1、温度为523 K、应变为8%的条件下(见图7(c))，晶体内部同时出现大量的第二相沉淀硬化的斑点状结晶。由于晶体内部晶粒细化和沉淀硬化的共同作用，使得材料塑性变形能力减弱，应变仅为8%。

4 热激活物理概念的本构关系

4.1 模型的建立

基于塑性流动热激活过程的位错运动学和动力学，结合材料的物理参数，建立一种物理概念的本构

图6 AZ31镁合金在不同试验条件下的微观结构Fig.6 Microstructures of AZ31 magnesium alloy under different testing conditions: (a) T=83 K, ε=1.0×10−3s−1, ε=10%; (b) T= 373 K, ε=1.0×10−3s−1, ε=11%; (c) T=573 K, ε=1.0×10−3s−1, ε=30%; (d) T=523 K, ε=1.0×10−1s−1, ε=40%

图7 AZ31镁合金在高应变速率下的微观结构Fig.7 Microstructures of AZ31 magnesium alloy at high strain rates: (a) T=523 K, ε=1.0×103s−1, ε=12%; (b) T=523 K, ε=5.0×103s−1, ε=16%; (c) T=523 K, ε=1.2×104s−1, ε=8%

模型来描述高应变速率下铸造镁合金AZ31在不同温度、不同应变速率下的塑性流动应力变化。首先，从金属的位错动力学角度考虑，金属和大多数合金的流动应力τ由两部分组成：热激活部分τ*(γ, γ, T)和非热部分τa(γ)。总的流动应力可表示为

非热部分τa(γ)与由于位错产生的弹性应力场、点缺陷、晶界和材料中杂质相关，不依赖于温度和应变速率。它通常取某个高温下的应力，超出这个高温后，流动应力变化很小。借助唯像学理论，基于材料的应力与应变的指数关系特性，取

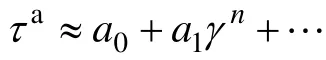
式中：a0，a1，…和n均为根据试验结果得出的参数。

热激活部分τ*(γ,T)为短程障碍对位错的阻力，是应变速率、温度和表征材料微观结构的一些内参量的函数。为了建立τ*与γ,T之间的数学关系，设位错必须克服的激活自由能为ΔG，基于位错运动学和动力学原理，借鉴KOCKS等[14]提出的关系式：

式中：0＜p≤1和1≤q＜2定义了短程障碍对位错的阻力构型，可以很好地描述塑性流动曲线的构型；τˆ为在0 K时的临界应力；G0是位错依靠自身的热能克服障碍的激活自由能。而塑性应变速率与ΔG的关系式借助于Orowan方程描述：

将式(2)和(3)合并得到

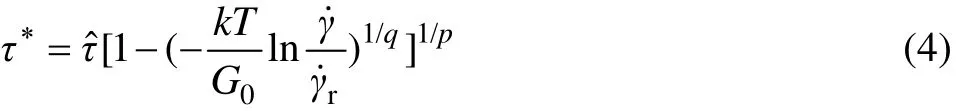
对于fcc 和hcp结构材料，材料的微观结构会随温度的变化而显著变化，具体表现为位错密度随塑性应变呈增长趋势。根据位错积累对流动应力的影响，NEMAT-NASSER和LI[15]提出了一个修正式：

式中：f(γ,T)=1+a0[1−反映的是微观结构演化(主要是位错密度)对流动应力的影响。由于位错密度与累积应变的对应关系，通过应变(单值增加)来等效反映位错密度的变化；a0取决于材料初始的微观结构；Tm为熔点温度。

结合式(5)，hcp金属的塑性流动关系通式可以由式(4)和流动应力非热部分τa(γ)统一表示为

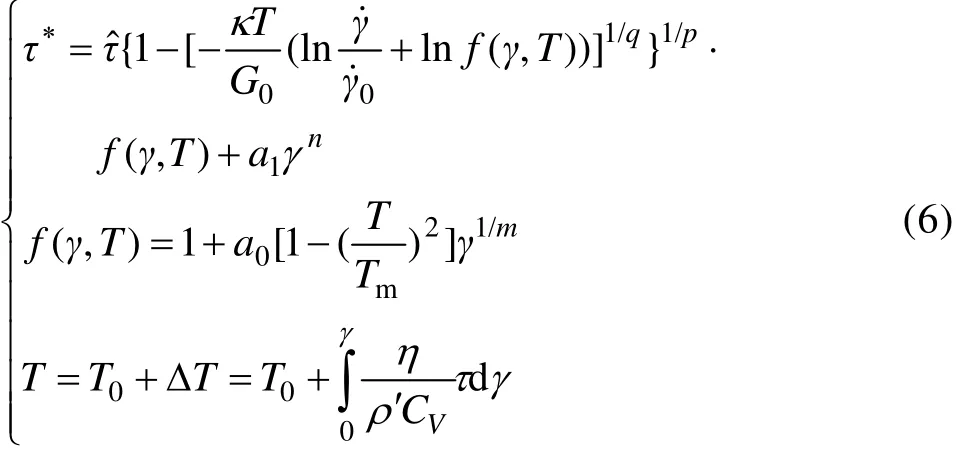
临界温度Tc由下式确定：

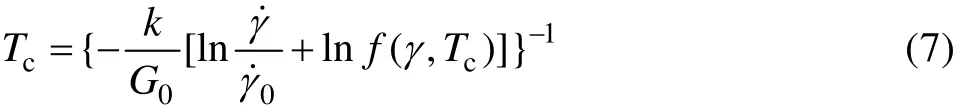
4.2 本构模型预测结果与试验结果的对比

结合式(6)和(7)，根据AZ31镁合金的物理参数，对于AZ31镁合金材料，其本构模型如下：

图8所示为在不同应变速率、不同温度下的模型预测结果与试验结果的对比。由图8可以看出：试验数据与模型模拟结果基本一致；在高应变速率1.2×104s−1时存在较大的误差。而由以上变形机理的微观分析可以知道，在此应变速率下，晶体内部出现大量沉淀析出物，即在一定程度上变形机理发生了改变。总体上，本模型可以较好地应用于AZ31镁合金材料在高应变速率下塑性流动应力的预测。

5 结论

1) 在低应变速率下，随着温度的升高，AZ31镁合金发生明显的由脆性到韧性的转化，其转化温度为473 K左右；当应变速率增加到1.2×104s−1时会发生脆化现象，合金的塑性变形能力变差。

2) 由变形机理的分析可知，在低应变速率下，晶体中孪晶的存在是促进材料塑性变形增强的主要因素；而在高应变速率下，动态再结晶和第二相粒子沉淀硬化将显著影响金属塑性变形。

3) 本文作者建立的基于物理概念的位错动力学本构模型可以较好地预测铸造镁合金AZ31在高应变速率不同温度下的塑性流动应力。经试验验证，模型模拟结果与试验数据吻合较好。

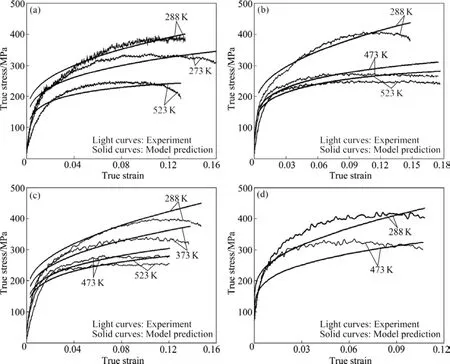
图8 不同温度、不同应变速率下模型预测结果与试验结果的比较Fig.8 Comparison of model predictions with experimental results at different temperatures and different strain rates: (a) 1.0×103s−1; (b) 3.0×103s−1; (c) 5.0×103s−1; (d) 1.2×104s−1

REFERENCES

[1] 余 琨, 黎文献, 王日初, 马正青. 变形镁合金的研究、开发及应用[J]. 中国有色金属学报, 2003, 13(2): 277−288. YU Kun, LI Wen-xian, WANG Ri-chu, MA Zheng-qing. Research, development and application of wrought magnesium alloys [J]. The Chinese Journal of Nonferrous Metals, 2003, 13(2): 277−288.

[2] 宁俊生, 范亚夫, 彭秀峰. 镁合金在大变形和高应变速率下塑性变形研究进展[J]. 材料工程, 2007, 9: 67−73. NING Jun-sheng, FAN Ya-fu, PENG Xiu-feng. Research and progress of plastic deformation of magnesium alloys at high strain rate and large deformation [J]. Engineering of Material, 2007, 9: 67−73.

[3] 陈振华, 夏伟军, 严红革, 李落星, 程永奇, 郭 强, 陈 鼎.变形镁合金[M]. 北京: 化学工业出版社, 2005: 48−171. CHEN Zhen-hua, XIA Wei-jun, YAN Hong-ge, LI Luo-xing, CHENG Yong-qi, GUO Qiang, CHEN Ding. Deformed magnesium alloy [M]. Beijing: Chemical Industrial Press, 2005: 48−171.

[4] 余 琨, 黎文献, 王日初. 镁合金塑性变形机制[J]. 中国有色金属学报, 2005, 15(7): 1081−1086. YU Kun, LI Wen-xian, WANG Ri-chu. Plastic deformation mechanism of magnesium alloys [J]. The Chinese Journal of Nonferrous Metals, 2005, 15(7): 1081−1086.

[5] 刘俊伟, 陈振华, 陈 鼎. 镁合金轧制板材低温变形行为与微观机制[J]. 中国有色金属学报, 2008, 18(9): 1577−1583. LIU Jun-wei, CHEN Zhen-hua, CHEN Ding. Microstructure evolution and deformation behavior of hot-rolled Mg alloy at low temperatures [J]. The Chinese Journal of Nonferrous Metals, 2008, 18(9): 1577−1583.

[6] 杨勇彪, 王富耻, 谭成文, 才鸿年. 镁合金动态力学行为研究进展[J]. 兵器材料科学与工程, 2008, 31(3): 71−74. YANG Yong-biao, WANG Fu-chi, TAN Cheng-wen, CAI Hong-nian. Research progress in dynamic mechanical properties of magnesium alloy [J]. Ordnance Material Science and Engineering, 2008, 31(3): 71−74.

[7] MAKSOUD I A, H AHMED, RODEL J. Investigation of the effect of strain rate and temperature on the deformability and microstructure evolution of AZ31 magnesium alloy [J]. Materials Science and Engineering A, 2009, 504: 40−48.

[8] 黄光胜, 汪凌云, 黄光杰, 卢志文, 宋美娟. AZ31镁合金高温本构方程[J]. 金属成形工艺, 2004, 22(2): 41−44. HUANG Guang-sheng, WANG Ling-yun, HUANG Guang-jie, LU Zhi-wen, SONG Mei-juan. Constitutive equation of AZ31 magnesium alloy for high temperature [J]. Metal Forming Technology, 2004, 22(2): 41−44.

[9] TAKUDA H, MORISHITA T, KINOSHITA T, SHIRAKAWA N. Modelling of formula for flow stress of a magnesium alloy AZ31 sheet at elevated temperatures [J]. Journal of Materials Processing Technology, 2005, 164/165: 1258−1262.

[10] SHENG Z Q, SHIVPURI R. Modeling flow stress of magnesium alloys at elevated temperature [J]. Materials Science and Engineering A, 2006, 419: 202−208.

[11] 郭伟国. BCC金属的塑性流动行为及其本构关系研究[D]. 西安: 西北工业大学出版社, 2007: 91−120. GUO Wei-guo. Plastic flow behavior and constitutive relation of BCC metals [D]. Xi’an: Northwestern Polytechnical University Press, 2007: 91−120.

[12] 郭伟国. 高温分离式Hopkinson压杆技术及其应用[J]. 实验力学, 2006, 21(4): 447−453. GUO Wei-guo. The split Hopkinson pressure bar technique of high temperatures and its application [J]. Journal of Experimental Mechanics, 2006, 21(4): 447−453.

[13] GUO Wei-guo. Dynamics strain aging during the plastic flow of metals [J]. Key Engineering Materials, 2007, 340/341: 823−828. [14] KOCKS U F, ARGON A S, ASHBY M F. Thermodynamics and kinetics of slip: Progress in materials science[M]. NewYork: Pergamon Press, 1975: 1−271.

[15] NEMAT-NASSER S, LI Y L. Flow stress of fcc polycrystals with application to OFHC Cu [J]. Acta Materialia, 1998, 46: 565−577.

(编辑 陈卫萍)

Plastic flow characteristics and physical conception constitutive relation for AZ31 cast magnesium alloy

SU Jing, GUO Wei-guo, HE Ke-xin, GE Yu-zhuo
(School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China)

The plastic flow properties of cast magnesium alloy AZ31 were studied at different strain rates and temperatures by using quasi-static testing machine and Hopkinson pressure bar equipment. The microstructure analysis of deformed specimen was carried out by means of the metallography microscope technique. The results show that, at lower strain rates, the transformation of AZ31 alloy from brittleness to toughness occurs with increasing temperature, and the transformation temperature is about 473 K. The brittleness phenomenon happens with increasing strain rate to 1.2×104s−1, and the plastic deformation capability becomes weak. Based on the microstructure analysis, the key factor of the plastic deformation enhancement at low strain rates is due to the existence of twinning in the crystal. At higher stain rates, however, the dynamic recrystallization and second phase particle precipitation hardness strongly affect the metal plasticity. Based on the thermal activation dislocation mechanism, paralleled with the system testing results, a plastic flow constitutive model with the physical conception was established. The model was used to predict the plastic flow stress at different temperatures and higher strain rates. According to comparing results, good agreement between the model predictions and experimental results is obtained.

AZ31 magnesium alloy; plastic flow; strain rate; microstructure mechanism; constitutive relation

TG146.2+2

A

1004-0609(2011)01-0044-07

国家自然科学基金资助项目(10872169)；爆炸科学与技术国家重点实验室基金资助项目(KFJJ08-11)；国家安全重大基础研究项目(613116)

2010-03-04；

2010-06-15

郭伟国，教授，博士；电话：13630283272；E-mail: weiguo@nwpu.edu.cn