EGNOS对流层延迟改正模型及其精度分析

刘靖晔，宋元明，胡加星

（桂林理工大学土木与建筑工程学院，广西桂林 541004）

EGNOS对流层延迟改正模型及其精度分析

刘靖晔，宋元明，胡加星

（桂林理工大学土木与建筑工程学院，广西桂林 541004）

对流层延迟是 GPS定位中一个主要的误差源，目前处理对流层延迟的主要方法是通过模型法、差分法等；当基线的距离较短时，基线两端气象条件基本相同差分法可以很好地修正对流层延迟误差，当基线的距离很长时，由于基线两端的气象参数差别较大差分法不能很好地消除对流层误差，模型法却能很好地消除对流层误差。对EGNOS模型进行了详细的介绍，并通过MATLAB编写程序；利用IGS跟踪站的数据进行计算分析比较，结果表明EGNOS对流层改正模型在高程上介于Saastamoinen模型和Hopfield模型之间，在x，y方向上精度相当。

GPS；对流层；EGNOS；精度分析

对流层紧邻地表，大气稠密，其高度为40 km以下的大气底层；由于折射率的变化，GPS信号穿过对流层时路径会发生弯曲，因此对GPS定位产生了偏差。天顶方向上的延迟可达2.3 m,天顶距离 z=80°时对流层延迟将增加至约13 m[2]。有关对流层延迟的改正方法,国内外的学者作了大量的研究,并提出了很多方法,如模型改正法、差分法、参数估计法等。在 GPS的各种定位中应用比较广泛的对流层改正模型有Hopfield模型、Saastamoinen模型、Black模型等。而投影函数有Marini(1972)，Chao(1974)，Davis(1985)及Niell(1996)等模型，其中Niell模型是目前高精度GPS定位中经常采用的一种投影函数[2]。在GPS数据处理中，对流层改正量总是与其他改正参数一起平差求得。实际证明，利用模型改正实测到的对流层天定延迟信息精密、可靠，精度可达 1-2 cm[5]。本文详细介绍了EGNOS对流层延迟改正模型，并与其他几种常用模型进行分析比较。

1 EGNOS天顶延迟改正模型及映射函数 [3-5][15]

EGNOS模型是欧盟的EGNOS（the European Geostationary NavigationOverly System）所采用的对流层天定延迟改正模型。EGNOS模型最大的好处就是计算天顶延迟时不需要实测的气象数据。该模型是基于接收机高度和 5个气象参数（气压、温度、水蒸气、温度下降率、水蒸气温度下降率）。这些参数利用多年的季节和时间数据的平均值，这些数值还与接收机所处的经纬度和时间有关系。

EGNOS模型也是分为干延迟和湿延迟两部分，任意方向上的对流层延迟可以用下式表示[6-7]：

式中,dtrop为对流层总的延迟量； ddry为对流层天顶方向的干延迟；dwet为对流层天顶方向的湿延迟；mdry为对流层干延迟的映射函数；mwet为对流层湿延迟的映射函数。

EGNOS模型的数学模型如下：

由平均海平面的天顶延迟计算接收机处的天顶延迟：

式中，g=9.80665m/s2；H是对海平面接收机高度（m）；T是对海平面的温度值 (K)； 是温度下降率 (K/m)；Rd=287.054 J/（kg.K）；水蒸气湿度下降率；Zdry是对海平面的“干”空气的延迟；Zwet是对海平面的“湿”空气的延迟。

式中，k1=77.604 K/mbar；P海平面气压（mbar）；gm=9.784m/s2。

式中，k2=382000K2/mbar；e是水蒸气压 (mbar)。

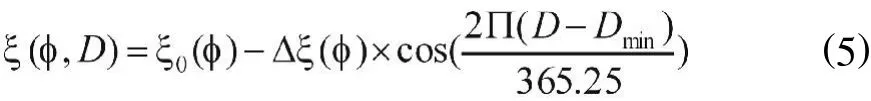
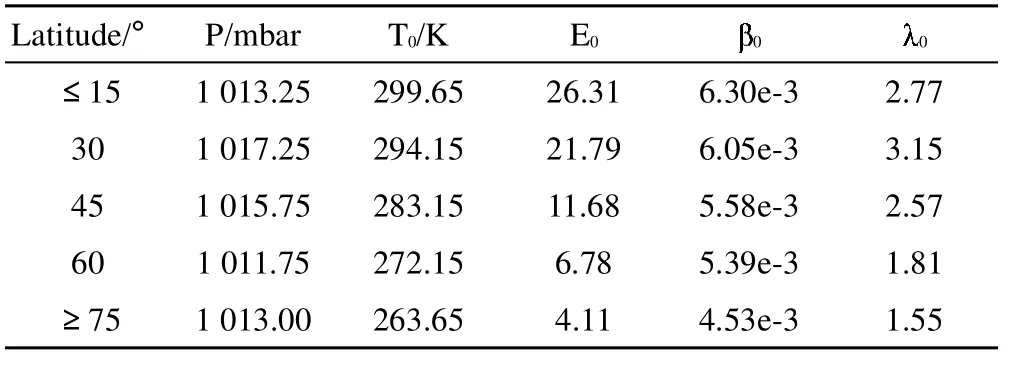
表1 EGNOS模型中的5个气象参数的年平均值

表2 EGNOS模型中的5个气象参数的季节变化值

其映射函数可以用下式表示：

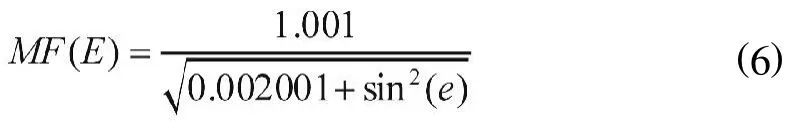
如果高度角低于 5°时，这个映射函数就不再适用了[4]。

2 常用的几种对流层延迟模型及映射函数

霍普菲尔德（Hopfield）模型[6][9-11]

萨斯塔莫宁 (Saastamoinen) 模型[6][9-11]

该模型的天顶方向的干湿延迟为：

式中，f(B，H)=1-0.002 66cos2B-0.000 28H；B测站纬度和测站H（km）高程。

公式（7）（8）中的可用下式计算[12]：

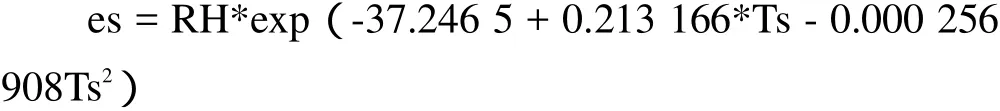
Niell映射函数模型[1][13]

Niell干延迟映射函数模型为:

式中，E为卫星高度角；H为测站高程 (m)；ahgt=2.53 ·10-5，bhgt=5.49·10-3，chgt=1.14·10-3；测站处的3个干延迟映射系数ahyd,bhyd,chyd可采用下式内插得到[13]。

Niell湿延迟映射函数模型为:

式中,E为卫星高度角;awet,bwet,cwet根据Niell湿延迟映射模型系数格网值内插得到。湿延迟模型不考虑时间因素,所以内插公式只与纬度相关,与年积日无关,得到内插公式为：

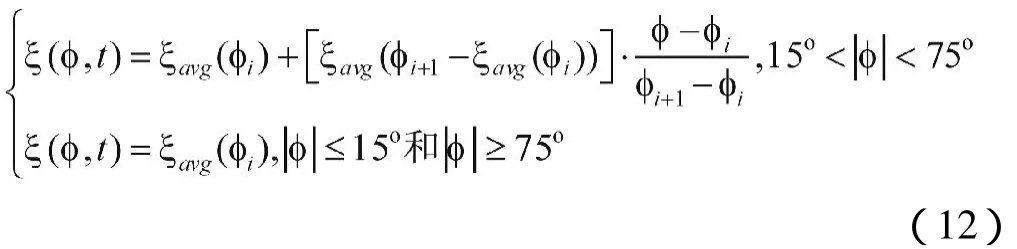
3 计算及结果分析

为了分析EGNOS模型在GPS定位中的精度，本文将EGNOS模型与目前精度比较高并广泛采用的Hopfield模型、Saas_Niell模型 (Saastamoinen天顶延迟模型和Niell映射函数的组合)在GPS普通单点定位中进行精度的分析比较。

为了实现各个模型的精度分析比较，本文采用了在 MATLAB 7.1里面编写程序，实现了普通单点定位的模块；Hopfield模型、Saas_Niell模型、EGNOS模型等3个对流层模块。在普通单点定位的模块中采取 C/ A码伪距、广播星历的Klobuchar模型进行电离层延迟改正,用多项式拟合卫星钟差。试验选取 BJFS(北京房山)和WUHN（武汉）两个IGS跟踪站的2009年第90天和第155天的观测数据，并用拉格朗日插值法求出相应的卫星坐标，用于单点定位的计算。各个模型间的3个方向的偏差如表3、表4所示，表中Saas-Hop表示Saas_Niell模型与Hopfield模型之差；Eg-Hop表示 EGNOS模型与 Hopfield模型之差；Eg-Saas表示EGNOS模型与Saas_Niell模型之差。

图1 各个模型在BJFS站155 d平面坐标互差图

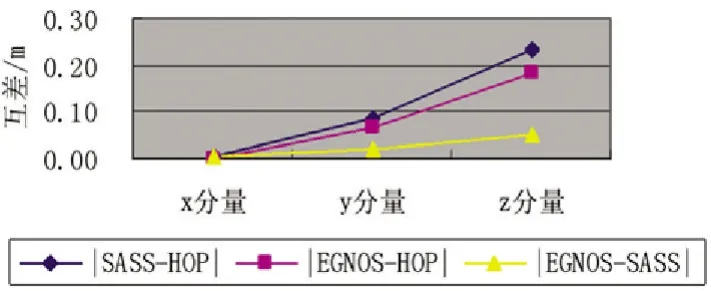
图2 各个模型在BJFS站90 d平面坐标互差图

图3 各个模型在WUHN站155 d平面坐标互差图

由图1-图3分析数据可看出各对流层改正模型在平面x方向的偏差约为1 cm，在平面y方向约为3 cm，在高程H方面偏差约为20 cm。还可以反映出EGNOS对流层延迟改正模型与Saas_Niell模型和EGNOS模型相比在x，y方向上的修正相当，在高程上介于Saastamoinen模型和Hopfield模型之间。分析影响各个模型精度的因素，都与气象参数密切相关；当测站处的气象参数未知时，都是用标准气象元素计算测站的气象元素。不同的算法直接影响到测站气象元素的精度，EGNOS模型则是利用全球（或某区域）平均海平面的各气象参数拟合求得，图1-图3的结果也说明EGNOS模型比Saastamoinen模型和Hopfield模型更能实际反映出测站气象元素。

4结 语

EGNOS模型是欧盟的EGNOS所采用的对流层天顶延迟改正模型。本文是在某一的气象条件下分析EGNOS模型、Saastamoinen模型和Hopfield模型对GPS定位精度的影响。利用IGS跟踪站数据多次计算分析得到，EGNOS对流层延迟改正模型与Saas_Niell模型和EGNOS模型相比在x，y方向上的修正相当，在高程上介于 Saastamoinen模型和 Hopfield模型之间。EGNOS模型采用全球（或某区域）平均海平面的各气象参数拟合测站实际的气象元素更于实际相符合。

[1] 施展,孟祥广,郭际明，等.GPS精密单点定位中对流层延迟模型改正法与参数估计法的比较[J].测绘通报,2009（6）：9-11

[2] 包海.GPS精密单点定位中对流层延迟改正模型的研究与分析[D].长沙：中南大学,2008

[3] 王新龙,李亚峰.GPS定位中四种对流层延迟修正模型适应性分析[J].电光与控制，2008，15（11）：5-9

[4] 朱国辉，张大鹏，戴钢，等.GPS定位系统中的几种对流层模型[J].全球定位系统，2006，4：36-38

[5] 曲伟菁，朱文耀，宋淑丽，等.三种对流层延迟改正模型精度评估[J].天文学报，2008，49:113-122

[6] 陈芳，高永梅，徐良骥，等.GPS测量误差中关于对流层延迟的探讨[J].西部探矿工程，2005（3）：26-27

[7] 严豪健,符养,洪振杰.现代大气折射论[M].上海：上海科技教育出版社，2006

[8] 付和宽，周本辰，蔡冰，等.大气延迟对GPS伪距单点定位影响的分析[J].地理空间信息，2010，8（3）：30-33

[9] 杨力,隋立芬.对流层传播延迟改正[J].测绘学院学报，2001, 18(3):182-185

[10]李征航,黄劲松.GPS测量与数据处理[M].武汉:武汉大学出版社,2005

[11]中国人民解放军总装备部军事训练教材编辑工作委员会.GPS技术与应用[M].北京：国防工业出版社，2004

[12]刘基余，李征航，王跃虎，等.全球定位系统原理及其应用[M].北京：测绘出版社，2004

[13]周命端，郭际明，孟祥广.GPS对流层延迟改正UNB3模型及其精度分析[J].测绘信息与工程，2008，33(4)：3-5

[14]John Paul Collins．Assessmentand Developentof a Tropspheric Delay Model for AircraftUsersof theGlobalPositioning System [D]．TechnialRepor，1999

[15]NigelPenna,A lan Dodson andWu Chen.Assessment of EGNOS Tropospheric Correction Model[J].Nigel Penna and Others,54：37-55

Delay Model and Accuracy Analysis of EGNOS Tropospheric

by LIU Jingye

Tropospheric delay in GPS positioning is a major source of error,in the handling of the main methods of tropospheric delay correction through model，difference method,etc,weakening or elimination of tropospheric delay error.When the distance is short baseline,baseline ends meteorological conditions are basically the same ,difference method can be very good correction troposphere delay error,when the baseline,due to the long distance between the meteorological data at baseline large, difference method can't eliminate the troposphere error well,but model can be a very good method to eliminate the troposphere error.In this paper,EGNOS model was introduced in detail,and through MATLAB programming.IGS tracking station data used to calculate statistical analysis,results showed that the EGNOS tropospheric correction model in elevation on the Saastamoinen model and the Hopfield model range, between the x,y direction precision.

GPS,tropspheric model,EGNOS,accuracy analysis （Page:96）

P228.41

B

1672-4623(2011)02-0096-03

2010-10-08

项目来源：国家自然科学基金资助项目（41064001）。

刘靖晔，硕士，主要从事GPS技术与应用方面的研究。