相空间重构在滑坡预测中的应用

汤 俊，邹自力，张晓平

（1.东华理工大学资环系，江西南昌 330013；2.东华理工大学地球科学与测绘工程学院，江西抚州 344000）

相空间重构在滑坡预测中的应用

汤 俊1，邹自力2，张晓平2

（1.东华理工大学资环系，江西南昌 330013；2.东华理工大学地球科学与测绘工程学院，江西抚州 344000）

针对滑坡位移时间序列的非线性特性，引入基于相空间重构和最小二乘支持向量机（LSSVM）的预测法。利用Cao氏方法确定嵌入维数，根据互信息法计算最佳延迟时间；然后在相空间中，利用最小二乘支持向量机（LSSVM）建立预测模型，对滑坡进行了实证计算，且与LSSVM模型和BP神经网络模型进行了比较。结果表明，模型具有较高的精度，是科学可行的。

滑坡预测；相空间重构；最小二乘支持向量机；神经网络

隧道现场监控量测是隧道施工的重要组成部分，在地铁施工过程中，无论是隧道内部的变形，还是对应隧道上方的地表变形，都是一个复杂的非平稳、非线性动态系统。如何从这些数据中提取出内在的规律性的东西，便成为工程技术人员面临的艰巨任务，其本质就是数据挖掘问题。基于这点认识，许多科技人员将隧道变形的实测数据进行常规分析和人工智能分析，并在此领域取得了丰硕的成果[1-4]。作为 SVM 近几年发展起来的新形式[5]，最小二乘支持向量机（LS-SVM）较好地解决了小样本、非线性、高维数、局部极小点等实际问题，在模式分类和回归建模等方面有较好的应用前景。经验模式分解EMD（EmpiricalModeDecomposition）是一种处理非线性、非平稳信号的新方法[6]，该方法吸取了小波变换的多分辨的优势，同时克服了小波变换中需要选取小波基的困难，是一种自适应的小波分解方法。

将 EMD和最小二乘支持向量机 LS-SVM（Least Square-SupportVectorMachine）相结合，对非平稳时间序列进行预测。首先运用EMD将非平稳的时间序列分解成具有不同特征尺度的本征式分量 IMF（Intrinsic Mode Function），然后根据IMF的变化规律，利用不同的LS-SVM建立不同的IMF分量预测模型。最后，所有分量的预测值组合重构得到最终的预测值。

1 经验模态分解（EMD）

HUANG等[7]提出将原始信号 EMD分解为若干IMF之和，从而赋予了瞬时频率合理的定义及物理意义，可用于非线性与非平稳信号处理[8]。

每个分解的IMF必须满足以下两个条件：1）极值点的数量与过零点的数量必须相等或最多相差不多于一个；2）在任一时间点上，信号局部最大值确定的上包络线和局部最小值确定的下包络线的均值为零。

EMD通过如下“筛选”过程来获得各个IMF：

1）设给定信号为 a，找出给定信号的局部均值，（这个过程可以通过取信号局部极大值的包络和信号局部极小值的包络的平均值来得到）将其局部均值组成新的序列m。a与均值序列m的差值被定义为序列h；

2）检查序列h是否满足IMF的基本条件或者满足给定的阈值，若满足则执行3）；否则，对信号继续执行步骤1）；

3）令ci=h，即h即为分解得到的第i个IMF分量ci；并令ri=ri-1-ci；

4）检查是否满足分解停止条件，若满足则执行5）；否则令a=r(i)返回1），i=i+1；

5）分解完成,得到基本模式分量 c1，c2，c3……，及残留分量rn。

最终，通过基于经验的模式分解得到：

式中，ci是从原始信号中获得的基本模式分量；rn为趋势项，即原始信号被分解为 n个基本模式分量和一个趋势项。c1～ cn就是原数据序列经分离后得到的不同尺度信息，c1中应包含原始信号中最短的周期分量，即信号尺度最小的部分；rn中包含信号中较大尺度的部分。因为尺度越来越大，所以 rn是一个相对缓变的信息，最终可能是一个单调函数，也可能是一个恒量。

2 最小二乘支持向量机（LSSVM）

预测建模问题实质上就是非线性回归问题。支持向量机的非线性回归的主要思想是：通过非线性映射(·)，将输入数据投影到高维特征空间（Hilbert空间），从而将低维非线性回归问题转化为高维特征空间中的线性回归问题。原理如下[9-11]：

构造最优决策函数：

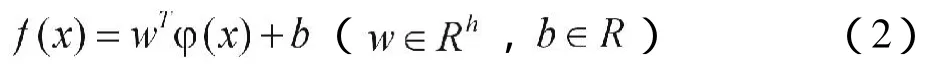
其中，h为高维特征空间维数（可能为无穷维），b为偏置量。

根据问题求解目标和结构风险最小化的原则，上式需满足如下条件：

根据LS-SVM算法，定义误差损失函数为误差的二次项，上述问题可转为

用拉格朗日乘子法求解这个具有等式约束的二次规划问题，定义Lagrange函数：

其中，ai和b为式 (8)的计算结果。

3 模型的构造

基于EMD和LSSVM预测模型，如图1所示。

图1 组合预测模型示意图

该模型的基本预测步骤如下：

1)采用EMD分解将非平稳信号分解为不同尺度的波动或趋势，各IMF分量分别包含了信号从高到低不同频率段的成分，且各分量都是平稳的；2)将各个IMF分量送入LSSVM进行预测，对每个时间序列都通过交叉验证法[12]得到最优参数，从而达到最佳的预测效果；3)所有分量输出后用各个分量的预测值重构出原始信号的预测序列。

4 仿真试验

4.1 EMD-LSSVM隧道不均匀沉降试验

数据来源于上海某隧道的监测项目，选取某一个监测点的沉降变化数据进行分析，观测周期为天，共有54期观测数据，趋势见图2，可以看出此序列有明显的非平稳特性。利用EMD-LSSVM模型对预测进行分析。

图2 原沉降时间序列

取前44期数据进行建模，将预测值与后10期真实值进行比较，预测误差采用平均绝对百分误差（MAPE）和相对误差（Pe）。其中，ri为实际负荷值，fi为预测负荷值，N为预测值总个数。

经EMD分解后，得4个本征模态分量和一个多余分量，如图3所示。

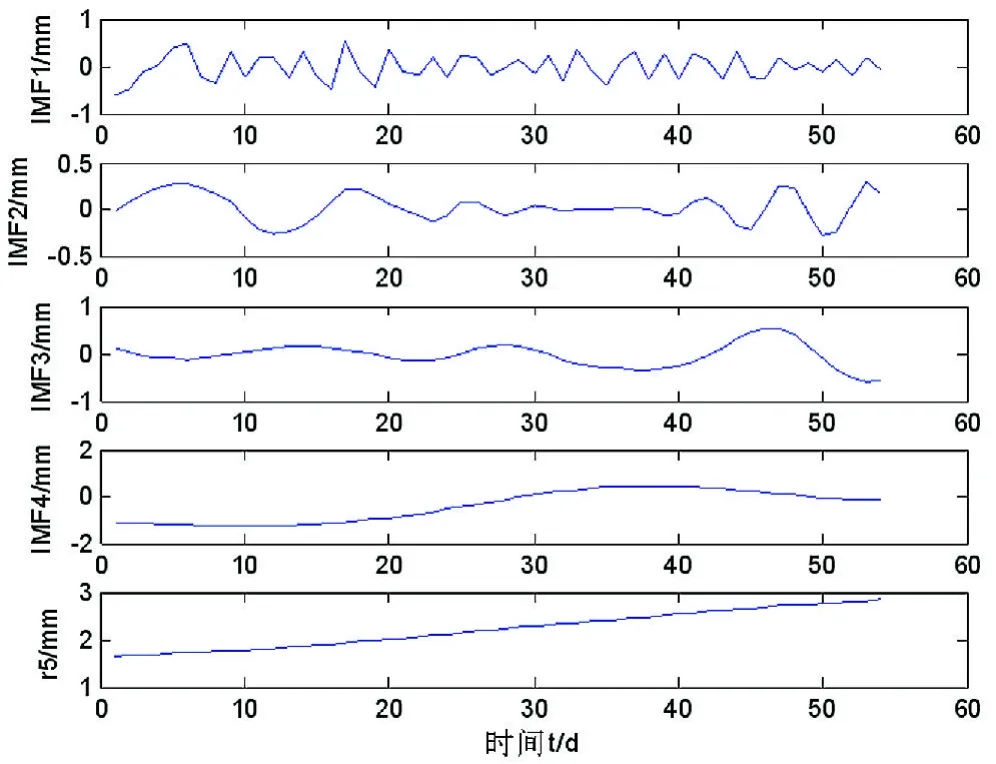
图3 原沉降时间序列及其各个分解分量

对各个分量采用不同的最小二乘支持向量机模型进行训练和测试，其核函数全部选用RBF核。经过试算，本文选取的最小二乘支持向量机模型参数的选择对预测结果的影响较大，这些参数包括核函数2和调节常数，因此参数的选择显得十分重要。利用交叉验证法得到最佳参数，各个分量对应的模型参数如表 1所示。

将各IMF预测序列合成重构，得到原序列的预测曲线如图4所示。

表1 各个分量LSSVM预测模型参数

图4 不同模型的不均匀沉降预测曲线比较

4.2 对比分析

分别采用自回归（AR）模型和单一的LSSVM模型对该组数据进行预测。其中，对于 A R模型，依据AIC推出了AR系列预报模型，得出AR(7)模型的结果最符合真实值；对于LSSVM模型，分别取核函数2=0.91290404和调节常数=5883.6819。得到预测曲线如图4所示。

可见，采用EMD-LSSVM模型后，曲线的拟合程度较之直接对序列进行AR(7)预测及用LSSVM预测有很大的提高，平均相对误差由19.6445%和9.4049%降至5.6033%，精度明显提高，3种模型预测结果见表2。

表2 三种模型的预测比较/mm

5结 语

对隧道不均匀沉降预测建模进行研究，利用EMDLSSVM的预测模型对其进行分析，得出以下结论：

1）采用EMD对原始沉降序列进行分解，得到一系列 IMF，并对其采用不同参数的最小二乘支持向量机建模预测，试验结果表明，该模型用于此是有效的。

2）通过与单一LSSVM模型和AR(7)模型进行预测对比，结果表明，该模型具有较高的精度。

3）在最小二乘支持向量机预测阶段，选取不同的参数，对预测结果影响较大；鉴于此，

采用交叉验证法选取参数，虽然耗时很长，但可以得到最优参数，从而大大提高预测精度。

4）将EMD-LSSVM用于隧道不均匀沉降预测，为此提供了一个新的解决思路。

[1] 尹光志，岳顺.基于ARMA模型的隧道位移时间序列分析[J].岩土力学，2009，30(9):186-191

[2] 韦凯，龚全美，周顺华.隧道长期不均匀沉降预测的蚁群算法[J].同济大学学报，2009，37(8):5-10

[3] 王金明.地铁隧道施工引起的地表沉降及变形研究[D]湖南:中南大学，2009

[4] 王穗辉，潘国荣.人工神经网络在隧道地表变形预测中的应用[J].同济大学学报，2001，29(10):1147-1151

[5] 邓乃扬，田英杰.数据挖掘中的新方法-支持向量机[M].北京:科学出版社，2004

[6]戴吾蛟，丁晓利，朱建军，等.基于经验模式分解的滤波去噪法及其在GPS多路径效应中的应用[J].测绘学报，2006，35(4): 27-33

[7]Huang NE，Shen Z，Long SR.The Empirical ModeDecom position and the Hilbert Spectrum for Nonlinear Non-stationary Time Series Analysis[J].Proc.R.Soc.Lond.A，1998，454:903-995

[8] 王军栋，齐维贵.基于EMD-SVM的江水浊度预测方法研究[J].电子学报，2009，10(10):20-23

[9] LiFangfang，Zhao Yingkai，Jiang Zhibing.The Prediction of Oil Quality Based on Least Squares Support Vector Machines and Daubechies Wavelet and Mallat A lgorithm[C].Proceedings of the Sixth International Conference on Intelligent Systems Design and Applications(ISDA0'6)，2006

[10]Zhang M ingguang，Li Zhanm ing，LiWenhu.IStudy on Least Squares Support Vector Machines Algorithm and its Application [C].Proceedingsof the17th IEEE International Conferenceon Tools，With Artificial Intelligence(ICTAI'05)，2005

[11]郑小霞，钱锋.基于PCA和最小二乘支持向量机的软测量建模[J].系统仿真学报，2006，18(3):739-741

[12]MommaM，BennettK P.A Pattern Search Method forModelSelection of Support Vector Regression[C].//Proceedings of the SIAM International Conference on Data M ining.Philadelphia: SIAM，2002:261-274

Prediction of Landslideby Phase Space Reconstruction

by Tang Jun

In view of the non linear characteristics of landslide disp lacement time sequence,introduced the prediction method based on phase space reconstruction and least squares support vector machine(LSSVM).Used Cao'sme thod to determine the embedding dimension,according to mutual information method to compute the best delay time;then in the phase space,used least squares support vector machine(LSSVM)to establish the forecast model to com pared with LSSVM and the neural network predictingm ode.The test result show s that them odelhas the high precision,is scientific and feasible.

landslide prediction,phase space reconstruction,least squares support vector machine,neural network （Page:139）

P258

B

1672-4623(2011)01-0139-04

2010-05-19

项目来源：东华理工大学校长基金资助项目（DHXK1010）；江西省数字国土重点实验室开放基金资助项目（DLLJ201014）。

汤俊，硕士，助教，主要从事变形监测和数据处理方向的研究工作。