Kelvin公式适用于微小气泡吗？

刘国杰 黑恩成

(华东理工大学化学系 上海 200237)

对于Kelvin公式是否适用于微小气泡这个问题，目前除了个别物理化学教材[1]外，大部分教材和表面化学专著都给出了肯定的答案：认为微小气泡中的饱和蒸气压小于平面液体的饱和蒸气压，且气泡的半径愈小，饱和蒸气压愈低。本文认为这是一个值得商榷的问题。

1 微小液滴的Kelvin公式推广

目前，大多数物理化学教材和表面化学专著，在叙述这个问题时，几乎都是从微小液滴入手，建立起Kelvin公式：

(1)

根据Laplace公式，液滴和毛细管中凸面液体的附加压力为：

(2)

式中pl和pg分别为液相和气相的压力。将式(2)代入式(1)，可得：

(3)

这些教材和专著推广了这个公式，认为只需对其进行简单修改，即可应用于气泡和毛细管中的凹面液体，因为它们的Laplace公式为：

(4)

如果将式(4)改写成：

(5)

并代入式(3)，便得：

(6)

这便是一般物理化学教材和专著推广所得的微小气泡和毛细管中凹面液体的Kelvin公式。

应该指出，这个推广对于毛细管中的凹面液体是顺理成章的，因为它与凸面液体的区别仅在于毛细管中液面的弯曲方向不同。但是，对于液体中的气泡，却不是那么简单，它还有一个稳定性的问题。

须知，一个气泡要在液体中稳定地存在，没有其他气体的帮助是不可能的，因为大的附加压力会使它迅速破灭。正是气泡的稳定条件会导致上述推广不再成立，换句话说，Kelvin公式 (式(6))是不适用于微小气泡的。若要建立液体在气泡中的饱和蒸气压公式，必须采用另外的方法。

2 液体在气泡中的饱和蒸气压

已知平面液体在温度T下达气液平衡时，饱和蒸气的压力为p*(图1(a))。若将蒸气分散在液体中，形成半径为r的微小气泡，且气泡离液面不远(图1(b))，则有两点必须指出：

① 液面上饱和蒸气的压力是不会因液面下存在微小气泡而改变的，其值仍然为p*，因为液面仍是平面。② 如上所述，如果气泡中没有其他气体存在，气泡是不可能稳定的，故为使气泡稳定，其中必须充入其他气体。

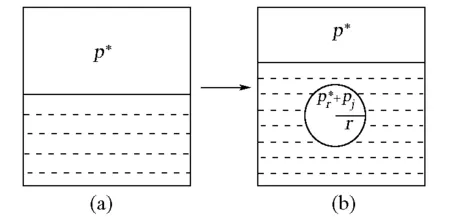
图1 液体的饱和蒸气压(a) 平面液体；(b) 微小气泡

倘若气泡内其他气体的分压为pj，则如图1(b)所示，气泡内气体的压力为：

(7)

(8)

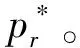
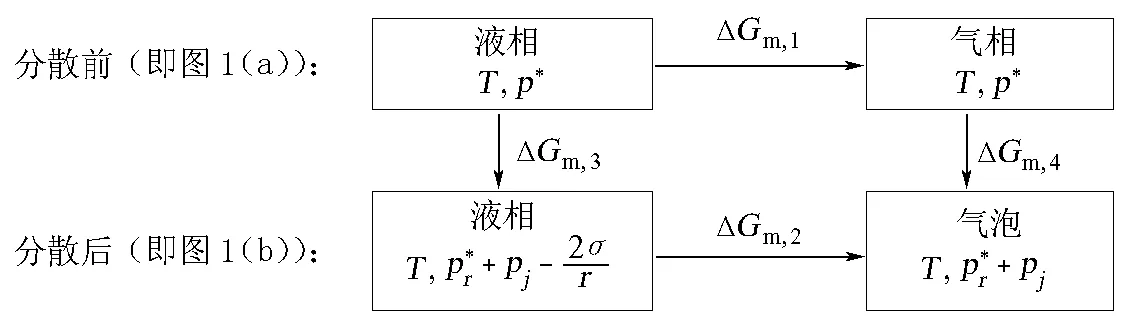
图2 微小气泡中液体饱和蒸气压的计算示意

由图1(b)不难看出，当气泡中充有分压为pj的其他气体时，气泡的稳定条件应为：

(9)

这就是说，气泡周围液体的压力

(10)

即为液面上饱和蒸气的压力，因此有：

ΔGm,3=0

(11)

又因分散前(图1(a))和分散后(图1(b))系统分别处在平衡状态，故ΔGm,1和ΔGm,2也都等于0。所以，只要蒸气可视为理想气体，便可得：

(12)

积分上限与气泡内是否存在其他气体无关，这是因为本文所选取的系统是液体及其蒸气，其他气体只是作为环境，系统状态函数的改变仅与系统的初、终状态有关。不难证明，对于液面上压力不是p*而是p外，即液面上有其他气体存在时，式(12)也同样成立。

由此可见，液体在气泡中的饱和蒸气压与平面液体的饱和蒸气压相同，即：

(13)

这就是本文所得结果。它已不再遵守Kelvin公式(式(6))，换句话说，液体在气泡中的饱和蒸气压仅是温度的函数，而与曲率半径无关。

同样的结论也可用下法导得：由于ΔGm,2=0，这相当于平衡的气液两相化学势相等，即：

μg=μl

(14)

(15)

液相的化学势因气泡周围液体的压力服从式(10)，其化学势应与平面液体相同，即：

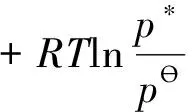
(16)

将式(15)和式(16)代入式(14)，得：

此式即式(13)。

3 毛细管中凹面液体的饱和蒸气压

类似的方法也可用于推导毛细管中凹面液体的饱和蒸气压。对于毛细管中的凹面液体，其Laplace公式也是式(4)，但不同的是，它能够稳定地存在，无须其他气体帮助(图3)，故不需要像式(9)那样的稳定条件。

图3 毛细管中凹面液体的饱和蒸气压

在凹面液体的上方，气相的压力为：

(17)

将式(17)代入Laplace公式(式(4))，可得到凹面附近液相的压力为：

(18)

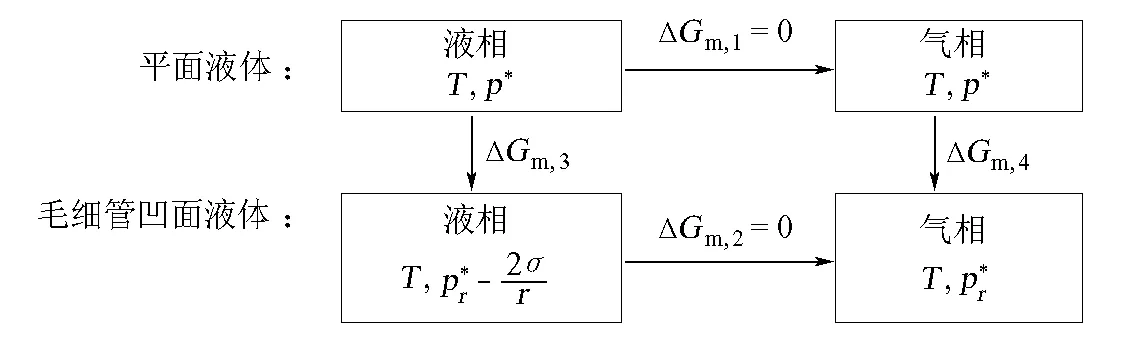
图4 毛细管中凹面液体饱和蒸气压的计算示意

由此可得：

ΔGm,3=ΔGm,4

(19)

其中

(20)

(21)

式中假定蒸气可视为理想气体。

将式(20)和式(21)代入式(19)，得：

这就是毛细管中凹面液体的饱和蒸气压公式，该公式即式(6)。

由此可见，液体中气泡与毛细管中凹面液体的饱和蒸气压分别遵守两个不同的关系式。

4 讨论与结论

利用上面所述的循环法也可求得微小液滴和毛细管中凸面液体的饱和蒸气压。

类似地，图5也可表示为图6所示循环。

图5 液体的饱和蒸气压(a) 平面液体；(b) 微小液滴

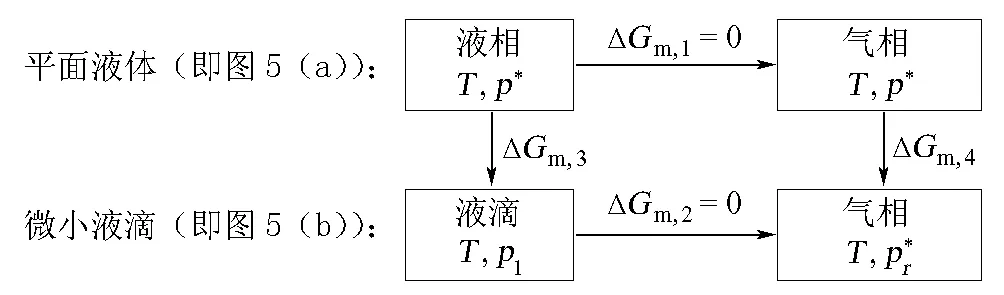
图6 微小液滴饱和蒸气压的计算示意

据此，可得ΔGm,3=ΔGm,4，即：

(22)

(23)

式(23)中液滴所承受的压力pl可由Laplace方程得到：

(24)

将式(24)代入式(23)，便不难得到Kelvin公式(式(1))：

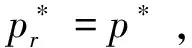
由此可见，微小液滴、微小气泡、毛细管中凸面和凹面液体的饱和蒸气压是否服从Kelvin公式，其关键就在于液相所承受的压力pl。这是基于热力学关系(∂μl/∂p)T=Vm，液相所受的压力愈大，其化学势愈大，作为物质传递的推动力，液体的逸出能力即饱和蒸气压也愈大，反之亦然。对于微小气泡，由于它要在液体中稳定地存在，必须在气泡中充入其他气体，这便要受稳定条件(式(9))的制约，致使气泡周围的液相压力变为p*，即等同于平面液体所受的压力，这便是微小气泡中液体的饱和蒸气压不再服从Kelvin公式的原因。

图7 298.15K时水的饱和蒸气压与界面曲率半径的关系

参 考 文 献

[1] 胡英,吕瑞东,刘国杰,等.物理化学.第5版.北京:高等教育出版社,2007