模糊二维线性鉴别分析算法

林宇生,房福龙,杨万扣

(1.中国电子科技集团公司第五十四研究所,河北石家庄050081;2.北京理工大学,北京100081;3.江苏省水利网络数据中心,江苏南京210029;4.东南大学,江苏南京210096)

0 引言

人脸识别是模式识别中一个重要的研究领域[1]。基于代数的人脸识别方法是当前人脸识别方法的主流,并且取得了较好的实验效果。在此类方法中,基于主成份分析(Principal Component Analysis,PCA)的特征脸识别方法[2]、基于线性鉴别分析(Linear Discriminant Analysis,LDA)的识别方法以及[3]二维线性鉴别分析(Two Linear Discriminant Analysis,2DLDA)[4]的识别方法使用较广。

在二维线性鉴别分析中,对于给定一个样本,在特征提取过程中的判别依据是要么这个样本属于某个类,要么不属于某个类,每次执行的是一个硬分类标准。而在特征抽取的具体问题中,由于当前训练样本往往受不同的表情和光照等复杂条件的影响,不能简单地将样本划入某一类。在模糊数学指导下,引入模糊隶属的概念,提出模糊二维线性鉴别分析,并运用于人脸识别中,取得了较好的识别率。

1 二维线性鉴别分析

线性鉴别分析方法的目的是从高维空间中提取出最具有分类能力的低维特征,希望投影后的特征数据在低维空间里不同类别间的样本尽可能分得开些,而每个类别内的样本尽可能密集,也就是说,样本类间离散度越大越好,而类内离散度越小越好。

设 ω1,ω2,…,ωc为c个模式类,{X1,X2,…,XN}为图像样本(Xi∈Rm×n),设每类含有样本数为li(∑li=N),图像类间散布矩阵Gb、类内散布矩阵Gw和总体散布矩阵Gt分别定义为:

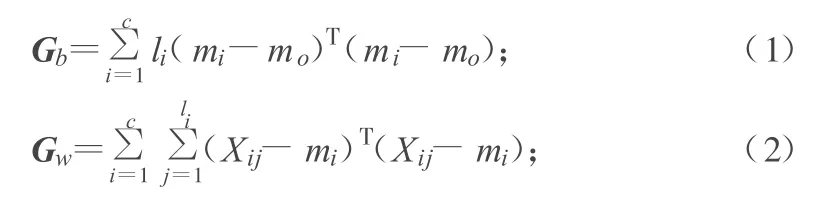
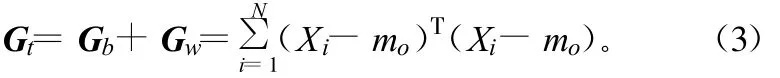
式中,mi为第i类训练样本的均值;mo为全体训练样本的均值。

由式(1)、式(2)和式(3)的定义知,Gb、Gw和Gt均为非负定矩阵。一般情况,类内散布矩阵是非奇异矩阵,最优的投影方向 WLDA就是使得样本类间散布矩阵和类内散布矩阵的行列式比值最大的那些正交特征向量。因此二维线性准则函数定义为:

通过线性代数理论,可知 W2DLDA就是满足式(5)的解:

二维线性准则函数通过求得矩阵(Gw)-1Gb大于零的特征值λi所对应的特征向量以得到投影空间,此时注意到该矩阵最多只有c-1个非零特征值,其中c为原始模式数据的类别数。

2 模糊二维线性鉴别分析

在二维线性鉴别分析中,构造散布矩阵时执行的是二值情况下的判别标准,即该样本或属于这类或不属于这类,每次执行的是一个硬分类标准。而在特征抽取的具体问题中,由于当前训练样本受表情和光照等复杂条件的影响,原始样本的分布通常是复杂的,若简单地将样本划入某一类的做法是不科学的。可以利用模糊C均值的思想,通过模糊隶属度函数表示样本的分布信息,进而给出模糊二维线性鉴别分析。首先利用模糊K近邻算法[5,6]得到相应的类中心点和隶属度信息,利用这些信息表示相应样本物理分布,并且将这些信息融入到特征提取过程中,得到更能代表原始样本的有效分类特征。

2.1 模糊K近邻方法

假定训练样本{X1,X2,…,XN}相应的向量形式为X=(x1,x2,…,xn),那么相应的模糊隶属度函数就表示了当前某一样本对于所有类别的依赖程度。设隶属度矩阵为 U=uij,其中 i=1,2,…,c,j=1,2,…,n。矩阵中的元素uij表示训练样本中的第j个样本对于第i类的依赖程度,并且这个隶属函数必须满足以下的2个条件:

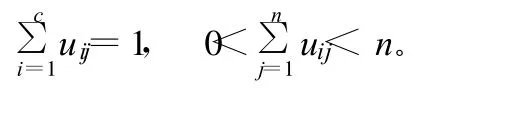
则相应的隶属函数可以通过模糊K近邻准则得到:

第1步,计算训练样本集中任意2个样本之间的欧氏距离,构成一个n×n的距离矩阵;

第2步,将得到的距离矩阵中对角线上的元素置为无穷大;

第3步,对上述步骤得到的距离矩阵的每一列按照距离值从小到大排列。根据新的距离矩阵得到k个最近邻点及这k个最近邻点的类别信息;

第4步,根据式(8)计算第j个样本跟第i类的隶属度。

式中,nij表示第j个样本的k个最近邻点中属于第i类的样本个数。

由此可以得到所有样本对于所有类别的隶属度函数。

2.2 模糊二维线性鉴别分析

根据各个样本对于各类的隶属度函数,重新计算样本的均值、模糊图像类间散布矩阵和模糊图像类内散布矩阵[5]。

至此得到所有新的散布矩阵,根据新的散布矩阵的定义,利用二维线性鉴别准则,得到相应的特征向量集,此时模糊二维线性鉴别准则如下:

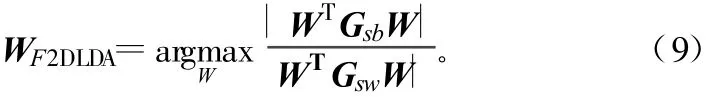
模糊二维线性准则函数通过求得矩阵(Gfw)-1·Gfb大于零的特征值λi所对应的特征向量来得到投影空间,矩阵中最多只有c-1个非零特征值,其中c为原始模式数据的类别数。

模糊二维线性鉴别准则在构造散布矩阵时将样本的隶属信息融入到相应的散布矩阵的定义中,因此可以抽取得到更有利于分类的鉴别信息。采用模糊二维线性鉴别分析方法比二维线性鉴别分析多了2步:一是隶属度函数的计算;二是根据隶属度函数重新计算散布矩阵。

基于模糊二维线性鉴别分析的算法如下所述:

第1步,根据模糊K近邻算法计算隶属度矩阵;

第2步,根据式(6)、式(7)和式(8)计算模糊图像类间散布矩阵 Gfb和模糊图像类内散布矩阵Gfw,计算(Gfw)-1Gfb前d个最大特征值对应的特征向量作为投影矩阵W;

第3步,将样本投影到 W,并进行分类。

3 实验分析

实验中分别用以下方法进行特征提取:PCA[2]、LDA[3]、文献[5]方法和新提出的模糊二维线性鉴别分析方法。分类器采用的是最小余弦距离分类器。在模糊K近邻算法执行过程中,可认为每个样本主要近邻为同类别剩余的样本,分类器采用最小余弦距离分类器。

3.1 实验1

在ORL人脸库上进行。ORL人脸数据库由40个人的脸部图像组成,每人由不同的10幅图像所构成,人脸图像原始维数为112×92像素。

实验中,在不同训练样本数目下,每次随机挑选S张用于训练,剩余图像用于测试。在LDA和文献[5]方法的第1步PCA变换和PCA中,保持95%的能量左右,循环10次得到的平均识别率如表1所示。

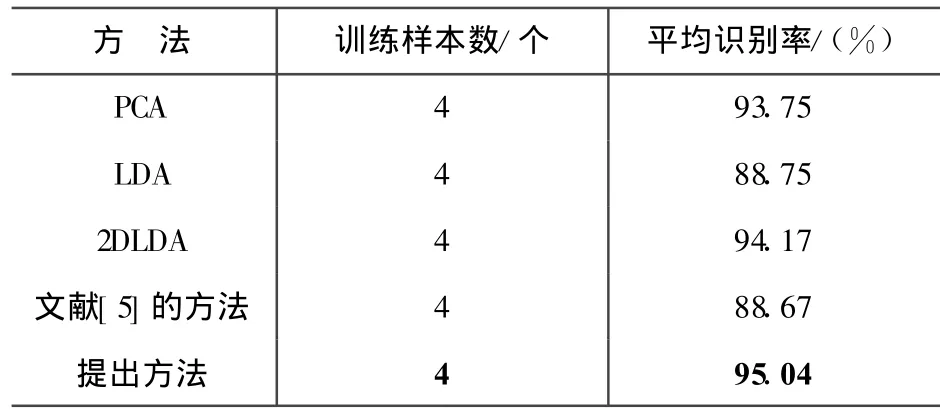
表1 在 ORL人脸库上的识别结果

从表1中可以看到模糊二维线性鉴别分析方法具有最高的识别率。能够取得如此好的识别率主要有以下2个原因:①在新定义的模糊类间散布矩阵和模糊类内散布矩阵中充分利用了样本分布信息,而在PCA和LDA中则没有考虑样本分布信息;②模糊二维线性鉴别分析方法考虑了样本的结构信息。

3.2 实验2

在耶鲁人脸库上进行。耶鲁人脸库中包括了15个人的165幅灰度人脸图像。每个人由11幅照片构成,这些照片在不同的表情和光照等条件下拍摄。实验中,图像维数被处理成100×80像素。

在实验中,每次随机挑选6张用于训练,剩余图像用于测试。在LDA和文献[5]的方法第1步PCA变换和PCA中,保持95%的能量左右。循环10次得到的平均识别率和标准方差如表2所示。从表2可以发现,新给出的方法仍然具有最优的识别结果。

表2 在耶鲁人脸库上的识别结果

4 结束语

二维线性鉴别准则在特征提取过程中使用的是一个硬分类标准,因此在样本分布比较复杂的情况下缺乏更有效的描述能力。提出的模糊二维线性鉴别分析吸收了模糊C均值的思想,通过隶属度函数将样本归入所有的类别之中,而不是简单的二值处理,并且将样本的原始分布信息通过相应的隶属度函数融入到最后提取到的特征之中,这样有效抑制了图像由于光照和表情等变换带来的影响,增强了算法的鲁棒性,提高了识别效率。

[1]李武军,王崇骏,张 炜,等.人脸识别综述[J].模式识别与人工智能,2006,19(1):58-66.

[2]TUR K M,PENTLAND A.Eigenfaces for Recognition[J].Journal of Cognitive Neuroscience,1991,3(1):71-86.

[3]SWETS D L,WENG J.Using Discriminant Eigenfeatures for Image Retrieval[J].IEEE Trans on Pattern Analysis and Machine Intelligence,1996,18(8):831-836.

[4]LI M,YUAN B.2D-LDA:A Statistical Linear Discriminant Analysis for Image Matrix[J].Pattern Recognition Letters,2005,26(5):527-532.

[5]KW K C,PEDRY W.Face Recognition Using a Fuzzy Fisher Classifier[J].Pattern Recognition,2005,38(10):1 717-1 732.

[6]KELLER J M,GR AY M R,GIVERN J.A.A Fuzzy k-nearest Neighbour Algorithm[J].IEEE Trans.Syst.Man Cybernet,1985,15(4):580-585.