盲信号分离及盲信号抽取研究

焦芳芳,封志宏,杨桂芹

(兰州交通大学电子与信息工程学院,甘肃兰州730070)

0 引言

盲信号分离技术是在源信号和混合过程未知的情况下,将混合信号中的源信号分离出来的一种方法。盲信号分离[1]的核心问题是分离(或解混合)矩阵的学习算法,其基本思想是抽取统计特征作为输入的表示,而不丢失信息。盲信号分离研究的信号模型主要有线性混合模型、卷积混合模型和非线性混合模型[2]。盲信号分离理论的发展可追溯到20世纪80年代初期。1985年,法国学者Herault和Jutten提出了一种使用简单的反馈网络结构的递推算法,使得盲信号分离从此成为了信号处理领域的一个研究课题。Tong等给出了完善的盲分离问题的数学框架并分析了盲分离问题的可分离性和不确定性,提出了基于高阶统计的矩阵代数特征分解方法。Comon系统地分析了瞬时混迭模型盲信号分离问题[3],明确了独立分量分析的概念。近年来,盲信号分离在图像处理和语音信号分离等方面的研究也逐渐引起国内研究者的关注[4]。凌燮亭等在国内较早地注意并且对盲分离进行大量的理论研究和实际应用研究。曹希仁对源盲信号分离的约束条件进行了深入的分析研究,理论上提出了分离问题的求解原则。何振亚等提出了一系列新的基于高阶统计及信息理论的判据和改进算法[5]。

盲分离的研究不断深化,新的理论算法不断被提出,盲信号混合模型也从开始的线性模型向多元化发展。近年来,盲分离的研究受到了国内外广泛的重视,理论研究和实际应用都得到了很大的发展。

1 盲信号分离问题的描述

1.1 盲信号分离问题的数学模型

盲信号分离的基本数学模型如图1所示。

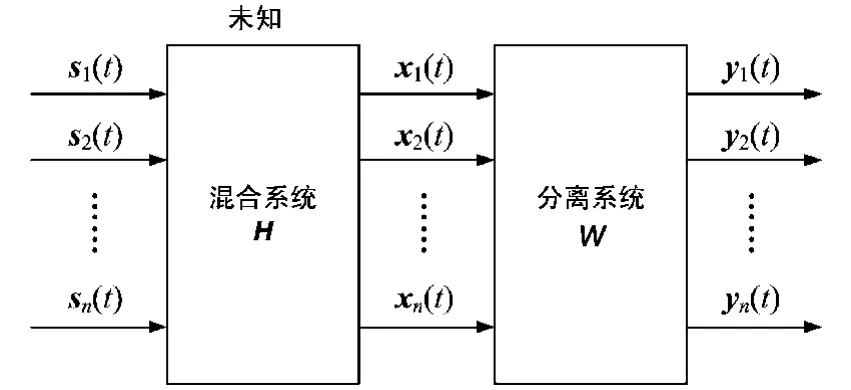
图1 盲信号分离的基本数学模型

盲信号分离可以用下面的混合方程描述[6]:

式中,s(t)=[s1(t),…,sn(t)]T,为n个源信号构成的n维向量;x(t)=[x1(t),…,xm(t)]T,为m 维观测数据向量,其元素是各个传感器得到的输出;m×n维矩阵H称为混合矩阵,其元素表示信号的混合情况,式(1)的含义是 n个源信号通过混合得到m维观测数据向量,盲信号分离的基本数学模型。盲信号分离问题的提法是:在混合矩阵 H和源信号未知的情况下,只根据观测数据向量x(t)确定分离矩阵W,使得变换后的输出为:

是源信号向量s(t)的拷贝或估计。

盲信号分离的最终目的就是寻找分离矩阵W,使输出信号y(t)尽可能逼近真实源信号 s(t)。混合矩阵H未知,且在没有任何源信号先验知识的情况下,源信号的恢复即是盲信号分离问题。

由式(1)和式(2)可知,y(t)是对源信号s(t)的估计,盲信号分离问题允许存在2个方面的不确定性:

①排列顺序的不确定性,无法了解所抽取的信号应是源信号s(t)的哪一个分量;

②信号幅度的不确定性,即无法知道源信号的真实幅值。

由于信号的信息很大一部分隐含在波形中,所以很多时候这2种不确定性并不影响盲信号分离技术的应用。

1.2 盲信号分离问题的前提假设

由于对源信号和混合矩阵无先验知识可以利用,因此必须对源信号和混合矩阵做出某些附加假设,不同的实际问题和不同的算法虽对源信号和混合矩阵所提出的假设不尽相同,但基本假设却是相同的,即源信号s(t)各分量si(t)相互统计独立,且其中最多只能有一个分量服从高斯分布(因多个高斯过程混合后仍是一个高斯过程,所以无法分离)。除此之外,还假设:

①源信号各分量为平稳随机过程。大多数算法都要求源信号为平稳的,对于非平稳信号的盲分离问题,文献[7,8]提出了多种方法;

②混合矩阵 H为可逆的或者为列满秩的(当n≤m时);

③si(t)是均值为零、方差为1的随机信号。此项假设是为了使盲分离过程变得简便。即使 si(t)的均值不为零、方差不为1,也可通过白化方法变其均值为零、方差为1。

2 盲信号分离算法的研究

2.1 盲分离的基本步骤和目标函数

盲信号分离的基本步骤如下:

①建立模型;

②建立目标函数;

③寻找算法。

首先根据所研究的问题建立模型;然后根据信息论和统计理论等方法建立一个以 W为变元的目标函数J(W),在不同的地方,目标函数或其期望值可能被称为代价函数(Cost Function)、损失函数(Loss Function)、对比函数(Contrast Function)或风险函数(Risk Function)等;最后是寻找一种有效的算法求解^W,例如标准梯度法、随机梯度法、自然梯度法以及其他启发式的学习算法等。若某个 ^W能使J(W)达到极大(或极小)值,即该 ^W为所求的解。

目标函数的构建有多种多样的方法,最基本建立目标函数的3种方法是:负熵、KL散度和最大似然目标函数。

2.2 盲信号分离的算法构造

盲信号分离的主要任务是估计一个分离矩阵,并由分离矩阵算出分离信号。一般情况下不可能求得分离矩阵的封闭形式的解,也就是说,不可能将它写成样本的某个确定函数,从而直接求得它的值。这时需要基于目标函数的自适应方法求解,具体过程是:首先对实际问题信源和信道进行分析,做出对信号源的统计性质与混合过程合理假设,建立盲源信号分离模型;然后,根据源信号的随机特征确定度量输出源分离结果的测度(非高斯性测度、信息测度、稀疏性的测度、平滑性测度和线性可预测性等)方法,以测度理论为依据分离准则,构造目标函数(也称代价函数),选定分离方法。在目标函数明确的情况下,可以使用任何经典的优化算法,如(随机)梯度算法和拟牛顿方法等进行优化,得到分离矩阵和信号源的估计。因此,盲源信号分离的核心问题可表示为:

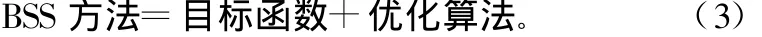
目标函数保证了盲信号分离实现可能性和实现途径,具体的目标函数还决定算法的统计性能;优化算法决定盲信号分离方法的性能。根据对源信号的假设条件源信号的分离方法有独立分量分析、稀疏元分析、主成分析和独立因子分析等。

2.3 盲信号分离的几种典型算法

盲信号分离代表性的算法主要有:Bell-Sejnowski最大信息量(Infomax)方法、Amari自然梯度(Natural Gradient)方法、Cardoso等变化自适应方法(EASI)、Hyvarinen快速独立元分析算法(FastICA)和矩阵特征值分解方法等。其他算法很多都是在这些算法的基础上推广或者补充发展起来的,当然盲分离并不仅仅局限于这些算法。盲分离中经常要用到优化运算,就优化手段而言,Infomax算法、自然梯度算法和EASI算法属于梯度下降(上升)优化算法,收敛速度是线性的,速度略慢一些,但属于自适应方法、具有实时在线处理能力;FastICA算法是一种快速而数值稳定的方法,采用拟牛顿算法实现寻优,具有超线性收敛速度,通常收敛速度较梯度下降寻优算法快得多;矩阵特征值分解盲分离方法通过对矩阵进行特征分解或者广义特征分解估计分离矩阵,是一种解析方法,可直接找到闭形式解(Closed Form Soutions),没有迭代寻优过程,因此运行速度最快。

3 盲信号抽取

从分离的过程上来看,盲信号分离方法有两大类:一类是前面提及的方法,同时将所有的信号都分离出来;另一类是每次只提取出一个信号(抽取过程),然后把这个提取出的信号在观测信号中的贡献去除(紧缩过程),不断重复这个过程,就可以将源信号逐次分离出来。将这类方法称作盲信号抽取(Blind Signal Extraction,BSE),其原理图如图2所示。

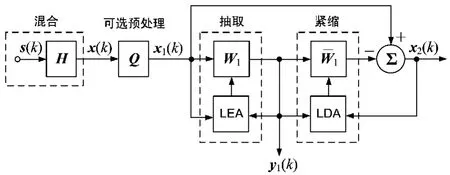
图2 盲信号抽取原理

假如源信号数目比较多,只对其中1个或几个信号感兴趣,就适合采用盲信号抽取方法。因为相对于同时把所有的源信号都分离出来的方法,盲信号提取方法有几个方面的优点:

①信号可以根据一个特征依次分离出来;

②可以只提取感兴趣的信号,对信号比较多的情况,有时候没有必要将它们全部分离出来,只要我们感兴趣的信号被提取出来以后,就可以终止整个提取过程;

③用于BSE的学习算法是局部的,与同时分离所有源信号的算法相比,算法更简单。

由于BSE算法在每提取出一个信号以后接着要做一个降阶的过程,以去除提取出的信号在原来输入信号中的贡献。这个降阶过程依赖于前面提取出的信号的准确度,随着降阶过程的不断进行,前面的误差会逐渐放大,从而使提取信号的准确度逐步下降。这是BSE算法的一个缺点。鉴于这一缺点,BSE算法还有待于进一步研究。

4 盲信号分离问题的研究方向

盲信号分离在最近几年已获得了长足的发展,提出了若干理论和方法,但还有许多问题有待进一步研究和解决,尤其是需要对以下问题进行研究:

①研究在性质未知的环境中的盲信号分离问题,即对非平稳、非高斯混合信号的盲分离问题的研究;

②卷积混合模型和对于更一般的非线性混合模型盲分离问题的研究较为复杂,所以研究能够在奇异混合情况下工作的盲分离算法是未来盲分离问题的发展方向;

③研究能够在非线性混合情况下工作的盲分离算法。对于带噪声混合信号的盲分离,现有的盲源分离算法和盲反卷积算法,大都假设无噪声或者把噪声看作一个独立源信号。如何将现有的盲分离算法推广到一般的噪声混合模型,是有待于进一步研究的问题;

④研究信号个数未知时能够工作的盲分离问题。由于各分量的排列顺序和幅值本身存在的不确定性,所以,如何按顺序输出以及只提取1个或多个感兴趣信号的盲分离问题研究是未来的研究方向之一;

⑤研究欠定或病态条件下的盲分离问。现有的盲分离问题都是假定信号个数一定的情况下进行的,源信号个数未知且可能动态变化时的盲信号分离问题的研究,观测信号个数比源信号个数多(少)的超(欠)定等问题的研究,特别是关于欠定问题的研究;

⑥研究混合矩阵不满足列满秩的情况下如何尽可能多地去提取源信号的盲分离问题,因为目前大多数算法都是在混合矩阵为列满秩的假设前提下完成的;

⑦因为现有的盲分离算法几乎都是单独考虑算法的某一方面的单一性能,对于其他方面性嫩,即对各种盲源分离算法的全局收敛性、渐近稳定性以及鲁棒性的研究也将是盲分离问题的研究方向之一;

⑧模糊系统理论在盲信号分离中的应用可能也是一个有前途的研究方向;

⑨与其他技术(如粒子滤波等)相结合的盲分离。

5 结束语

盲信号分离是解决阵列处理和数据分析中的一个典型问题,经过学者们的共同努力,盲分离的理论和算法得到了较快发展,提出了一些在分离能力、内存需求和计算速度等方面性能各异的算法。盲信号分离的发展对信号处理起到了极大的推动作用,要进一步发挥其作用,许多理论问题和算法的研究还有待进一步解决,并且需要进一步探索盲分离理论与实际应用的契合点。

[1]张贤达,保 铮.盲信号分离[J].电子学报,2001,29(12A):1766-1771.

[2]李小军,朱孝龙,张贤达.盲信号分离研究分类与展望[J].西安电子科技大学学报:自然科学版,2004,31(3):399-404.

[3]COMMON P.Independent Component Analysis,A New Concept[J].Signal Processing,1994(36):287-314.

[4]马建仓,牛奕龙,陈海洋.盲信号处理[M].北京:国防工业出版社,2006:1-273.

[5]李荣华,赵 敏,王 进.盲信号分离的理论与发展现状[J].移动通信,2008,32(8):67-72.

[6]何继爱,王维芳,李力舟.盲信号分离方法研究[J].无线通信技术,2009,35(4):10-14.

[7]PARRA L,SPENCE C.Convolutive Blind Source Separation of Nonstationary Sources[J].IEEE Trans.Speech Audio Processing,2000(10):320-327.

[8]PHAM Dinh-tuan,CARDOSO Jean-francois.BlindSeparationof Instantaneous Mixtures of Nonstationary Sources[J].IEEE Transactions on Signal Processing,2001,49(9):264-269.