使用伪氨基酸组成和BP神经网络预测类弹性蛋白多肽的相变温度

黄凯宗,张光亚

(华侨大学化工学院,福建泉州 362021)

使用伪氨基酸组成和BP神经网络预测类弹性蛋白多肽的相变温度

黄凯宗,张光亚

(华侨大学化工学院,福建泉州 362021)

根据获得的16条ELP序列及相变温度的数据,利用伪氨基酸组成方法提取其序列特征值.将伪氨基酸组成中的相关系数部分作为类弹性蛋白的特征向量,从类弹性蛋白序列出发,利用最小中位方差回归,找出与其序列相关系数的最佳阶数.运用均匀设计法,分别对支持向量机与BP神经网络参数进行优化.结果表明:BP神经网络获得的预测模型最佳,相变温度绝对误差为0.39℃,均方根误差为0.89℃.

类弹性蛋白;相变温度;伪氨基酸组成方法;支持向量机;BP神经网络

类弹性蛋白多肽(Elastin-Like Polypep tides,ELPs)是一种具有弹性功能且对环境非常敏感的生物高分子,它由五肽重复序列单元构成.如果环境温度低于ELP的相变温度,则该多肽在水溶液中是高度可溶的,聚合物链就保持无序结构,且相当伸展;反之,当环境温度高于相变温度时,这一含水的多肽链结构就会瓦解,并开始聚集,形成一个富含 ELPs的聚集物[1].利用类弹性蛋白的可逆相变特性,使其在蛋白纯化、药物载体、组织工程等方面得到广泛的应用[2].U rry等[3]认为,相变温度是关于 ELP序列、多肽链长度、Xaa种类摩尔分数的函数.Chilkoti等[4]利用重组基因进行克隆表达,得到了在序列和多肽链长均能精确控制的ELP.他们用非线性回归分析描述了ELP序列链长及浓度与相变温度的关系,但所得到的模型仅能预测3种ELP文库的相变温度.本文根据获得的16条ELP序列及相变温度的数据,利用伪氨基酸组成方法提取其序列特征值,采用BP神经网络、支持向量机方法、最小中位方差回归预测ELP的相变温度值.

1 材料与方法

1.1 试验数据来源

文中所用的数据取自于文献[5].

1.2 伪氨基酸组成

伪氨基酸组成包含20+λ个变量,最早由Chou等[6]提出.由于文中所涉及的ELP氨基酸组成极为相似,而且种类很少,为了减少输入变量数目,对其略作调整,仅取其后的λ个变量,即氨基酸相关系数. ELP相关系数的阶数λ从1取到10,氨基酸相关系数计算参见文献[7].

1.3 均匀设计

在运行时,支持向量机(SVM)[8]和BP神经网络[9]都需要选择参数,以达到最佳效果.因此,采用均匀设计法(UD)[10]来选择适当的运行参数.定义3个特征指标[11],即平均绝对百分比误差δMPAE、均方根误差δMSE和平均绝对误差δMAE.模型预测的结果采用常用的“留一法”,即对n组数据,每次取1组作测试,其他n-1组作为训练样本,共进行n次循环,使得样本中所有数据都能进行预测.

2 结果与分析

2.1 氨基酸相关系数的阶数的选择

根据文献[6],氨基酸相关系数的阶数(λ)是伪氨基酸组成一重要参数.文献数据的相变温度呈离散分布,使用最小中位方差回归会更为精确[11-12],且运行过程中无需调整参数.

参数λ经最小中位方差(Least Median of Squares Regression,LM SQ)回归检测,获得的平均绝对百分比误差δMPAE、均方根误差δMSE和平均绝对误差δMAE关系,如表1所示.由表1可知,当λ=8时,δMAE为3.04,δMSE为5.73,δMPAE为40.91%.即拟合所得ELP相变温度准确率最高,因此取λ=8.

表1 氨基酸相关系数的阶数对特征指标的影响Tab.1 Effect of the o rder of correlation coefficient for amino acids on characteristic index

当λ=8时,执行最小中位方差回归得到ELP的相变温度拟合模型为

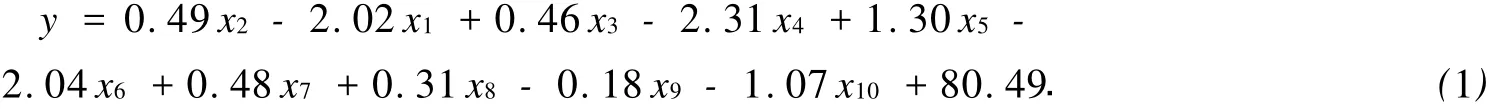
其中:x1～x8分别为伪氨基酸组中相关系数;x9～x10分别为 ELP的相对分子质量、ELP每一单体的Xaa数量;ELP浓度对ELP相变温度没有影响,故为其相关系数零.

从模型(1)可见,第1,第4和第6个相关系数对相变温度有较大的负面影响,而第5个相关系数则有较大的正面影响;伪氨基酸组的相关系数对ELP的相变温度影响较大.当ELP浓度较高时,其浓度在一定范围变化对相变温度几乎不影响.这与Chilkoti等[4]的实验结果较为一致.

使用最小中位方差回归获得的拟合值与实测值关系,如图1所示.由图1可知,一些拟合值非常好,而另外一些预测值与实测值差距比较大,从而导致其回归直线的斜率偏离较大.

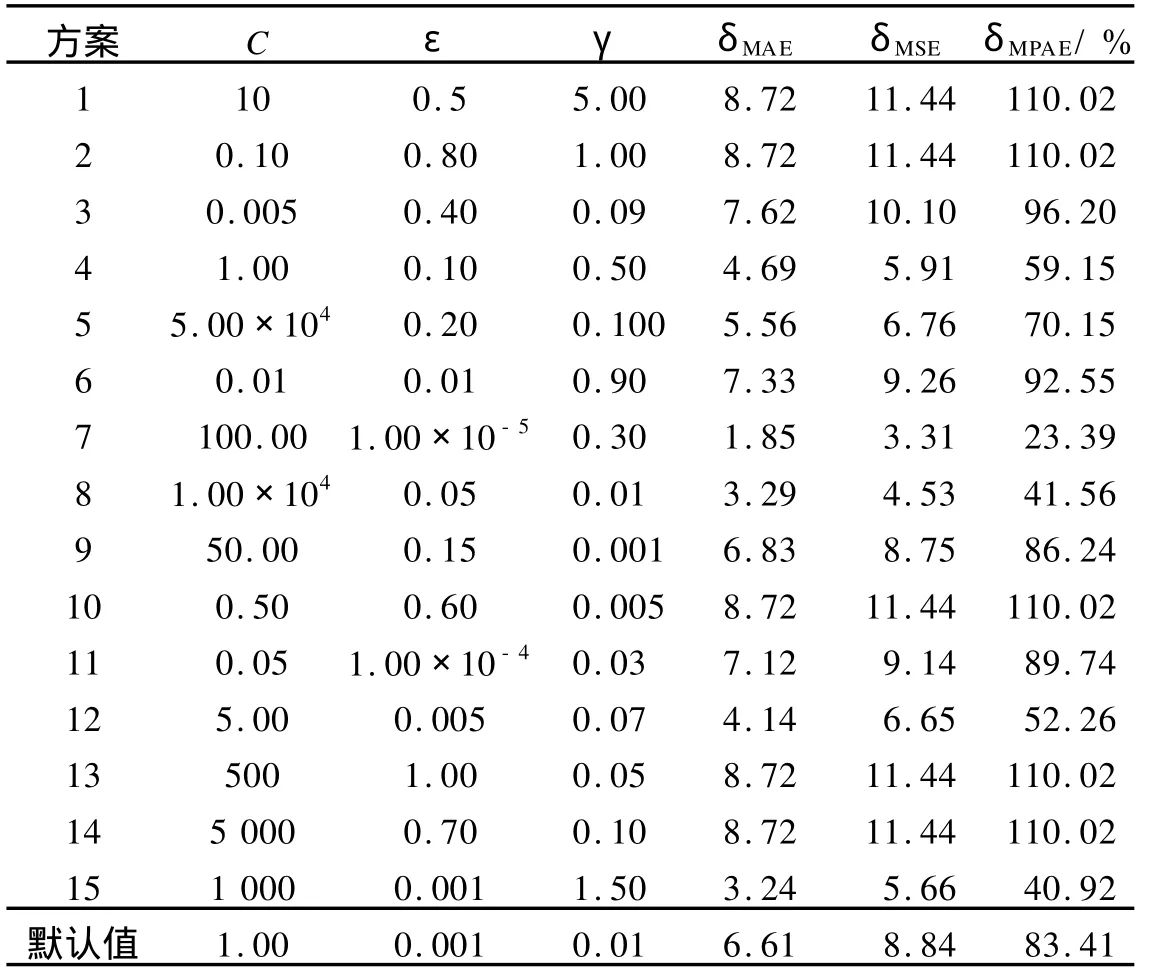
表2 支持向量机运行参数的选择Tab.2 Selection of running parameters of SVM

2.2 利用支持向量机预测相变温度

如前所述,λ=8为氨基酸相关系数的阶数最佳运行参数.利用均匀设计法对支持向量机的运行参数进行优化,交叉验证后的结果如表2所示.

由表2可得出,3个误差特征指标在交叉验证中变化的幅度较小.这说明SVM对运行的参数不是很敏感.当惩罚系数C=100,ε为1.0×10-5,γ为0.3 (即方案7)时,其δMAE,δMSE和δMPAE值均最小,分别为1.85,3.31和23.39%.即所建立的模型对 ELP相变温度预测准确率最高,故为最佳方案.

在方案7中,使用用支持向量机方法建立相变温度模型.通过该模型对实际测得的数据进行预测,预测的效果,如图2所示.从图2可知,模型预测的结果

与实际测量值的相关系数达0.93,模型预测的结果较好.

2.3 利用神经网络预测相变温度

对神经网络而言,由于训练样本集的大小有限,网络训练后对训练集外的输入的响应,直接决定网络的性能.为了检验所建立的神经网络的可靠性,对其进行3因素9水平交叉验证,结果如表3所示.

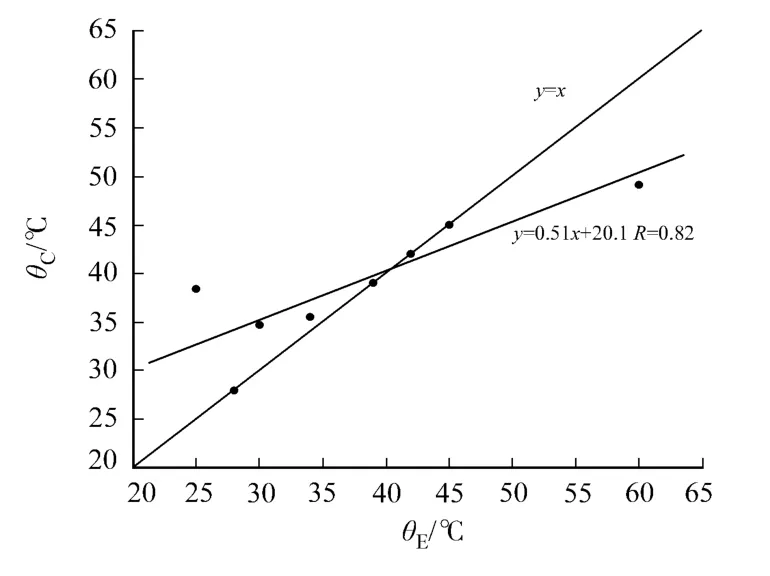
图1 利用最小中位方差回归的拟合值与实测值关系Fig.1 Relationship between experimental and fitted transition temperature obtained by LM SR

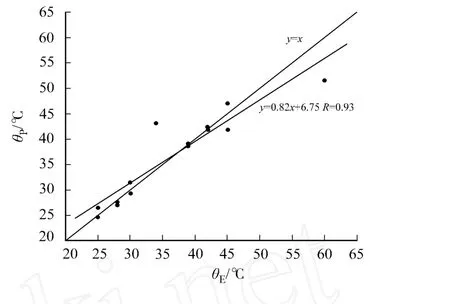
图2 使用支持向量机获得的预测值与实测值关系 Fig.2 Relationship between experimental and predicted transition temperature obtained by SVM

从表3可知,3个特征值变化幅度较大,神经网络对运行参数比较敏感.在9组验证中,采用默认参数获得的特征值最好.即隐含层节点数(n)为6,学习速率(v)为0.3,动态参数(σ)为0.2时,准确率最高,其δMAE,δMSE和δMPAE值均最小,分别为0.39,0.89和4.86%.

用BP神经网络建立的相变温度模型.通过该模型对实际测得的数据进行预测,结果如图3所示.从图3可知,模型预测的结果与实际测量值的相关系数达0.99.

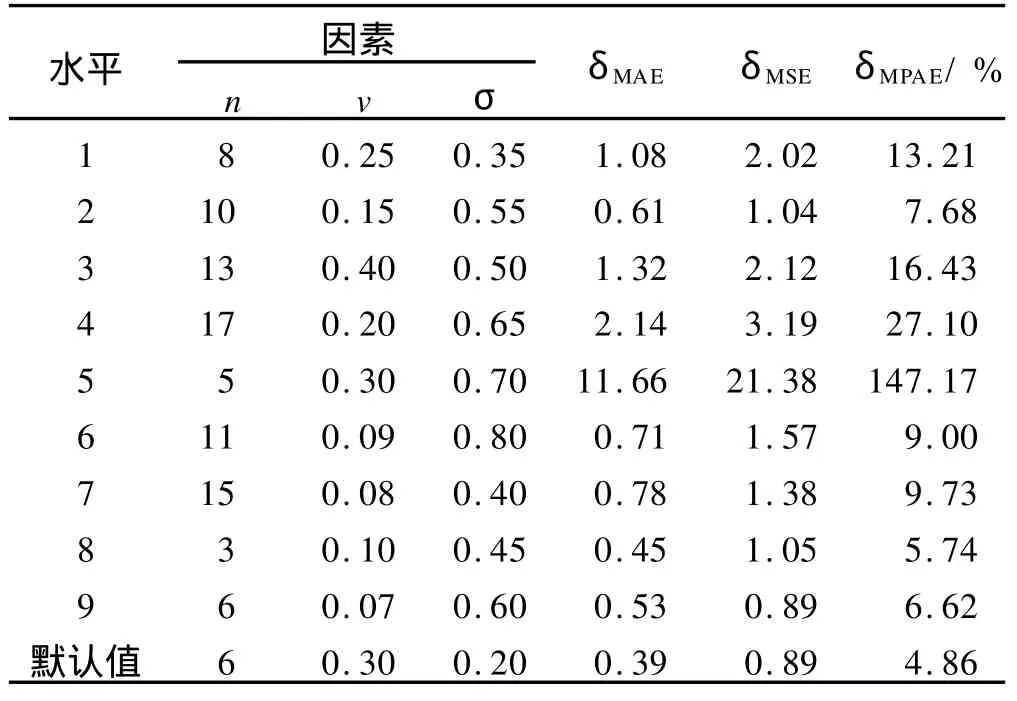
表3 神经网络运行参数的选择Tab.3 Selection of running parameters of BP neural network

图3 使用BP神经网络获得的预测值与实测值关系Fig.3 Relationship between experimental and predicted transition temperature obtained by BP neaural network

3 讨论

由图1～3可知,BP神经网络所建立的预测相变温度的精度,比使用支持向量机和最小中位方差回归建立的相变温度要好,可作为后续使用的模型.

当实测的ELP相变温度为60℃(此时ELP的序列最短浓度最高),与3种算法所预测(回归的结果是拟合的)出来相变温度值均差距较大.这可能是因为当序列较短时,ELP浓度与长度的变化对相变温度影响更大[4],而ELP的序列组成对相变温度影响较小.

与传统的拟合方法预测ELP的相变温度相比,基于支持向量机和神经网络对相变温度进行预测,不用通过预测相变温度具体形式,就可以直接从数据中得到相变温度与ELP序列、分子量、Xaa组成、浓度之间的关系.同时,只要能加以一定的先验知识,还能够更大范围地反映它们之间的关系,其应用的范围也将更为广阔.

文中基于Chou等提出的伪氨基酸概念[6],考虑到ELP的氨基酸组成极为相似,构造了一种λ维的伪氨基酸组成来表示蛋白质序列.采用BP神经网络、支持向量机方法、最小中位方差回归预测ELP的相变温度值.结果表明,当λ=8为氨基酸相关系数的阶数最佳运行参数时,使用BP神经网络所建立的相变温度预测模型为最佳.

[1]URRYDW.Physical chemistry of biological free energy transduction as demonstrated by elastic protein-based polymers[J].Phys Chem(B),1997,101(51):11007-11028.

[2]CHOW D,NUNALEE M L,CH IL KOTIA,et al.Pep tide-based biopolymers in biomedicine and biotechnology [J].Mater Sci Eng R Rep,2008,62(4):125-155.

[3]URRYD W,LUAN C H,PARKER T M,et al.Temperature of polypep tide inverse temperature transition depends on mean residue hydrophobicity[J].J Am Chem Soc,1991,113(11):4346-4348.

[4]M EYER D E,CH ILKOTIA.Quantification of the effects of chain length and concentration on the thermal behavior of elastin-like polypep tides[J].Biomacromolecules,2004,5(3):846-851.

[5]OlSON SD.Mathematical models for analysisof tissue regeneration in articular cartilage[D].No rth Carolina State: North Carolina State University,2009.

[6]CHOU Kuo-chen.Prediction of protein cellular attributes using pseudo amino acid composition[J].Proteins:Structure,Function,and Bioinfo rmatics,2001,43(3):246-255.

[7]SHEN Hong-bin,CHOU Kuo-chen.PseAAC:A flexible web-server for generating various kinds of protein pseudo amino acid composition[J].Analytical Biochemistry,2008,373(2):386-388.

[8]VANPN IK V N.The nature of statistical learning theory[M].New York:Sp ringer-Verlag,1995.

[9]黄永恒,曹平,汪亦显.基于BP神经网络的岩土工程预测模型研究[J].科技导报,2009,27(6):61-64.

[10]方开泰.均匀设计:数论方法在试验设计的应用[J].应用数学学报,1980(3):363-372.

[11]张光亚,葛慧华,方柏山.一种预测木聚糖酶最适温度的PCANN模型[J].华侨大学学报:自然科学版,2007,28 (1):55-58.

[12]ROUSSEEUW PJ.Leastmedian of squares regression[J].Journal of the American Statistical Association,1984,79 (388):871-880.

[13]STEELE JM,STEIGERW L.Algorithms and complexity for least median of squares regression[J].Discrete Applied Mathematics,1986,14(1) :93-100.

(责任编辑:黄晓楠英文审校:刘源岗)

Using Pseudo-Amino Acid Composition and BP Neural Network to Predict the Transition Temperature of Elastin-Like Peptides

HUANG Kai-zong,ZHANG Guang-ya
(College of Chemical Engineering,Huaqiao University,Quanzhou 362021,China)

Elastin-like pep tides(ELP)is one of the multi-pep tides which has been widely used.Transition temperature is the most convenient parameters for quantificational description of the ELP properties.It is of great importance to exp lo re the relationship between the transition temperature and the sequence characteristics,the number of Xaa of each monomer and the concentration of ELP.In this article,the best order of the correlation coefficient for pseudo-amino acid composition was obtained by using Least Median of Squares Regression from sequence.The uniform design was used to optimize the running parameters and leave-oneout cross-validation was carried out to evaluate the model of back propagation neural network(BPNN)and support vector machines,respectively.The results showed that the predicted model obtained by BPNN was the best,of which the mean absolute error and root mean squared error was0.39℃and 0.89℃, respectively.

elastin-like pep tides;transition temperature;pseudo-amino acid composition;support vector machines; back propagation neural network

Q 516.02

A

1000-5013(2011)02-0194-04

2009-09-21

张光亚(1975-),男,副教授,主要从事生物信息与生物化工的研究.E-mail:zhgyghh@hqu.edu.cn.

国家自然科学基金资助项目(20806031);福建省自然科学基金资助项目(2009J01030)