钢锭锻造用套筒套的设计与计算

曹志远 季 雪 程幸叶 牛广斌

(天津重型装备工程研究有限公司，天津300457)

套筒是大型钢锭自由锻造时不可缺少的锻造附具，其与钢锭的钳口配合在天车配备的翻钢机的带动下来实现钢锭的移动和旋转。随着工业的发展和锻压水平的提高，水压机锻造钢锭的最大吨位也由200 t级向更大吨位迈进，即使新型水压机配备了大型操作机也不能完全替代套筒这种传统的锻造附具，所以有必要设计更大吨位级的套筒。

1 按照悬臂梁假设推导公式

钢锭尺寸示意图见图1，锭身重量与重心的计算公式如下：

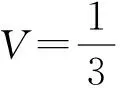
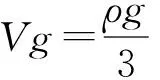
假设钢锭钳口与翻钢机套筒紧密接触，可认为钢锭是一个悬臂梁，如图2所示。

外载荷：M=Gh2，Q=G

(1)弯曲正应力

最大弯曲正应力：

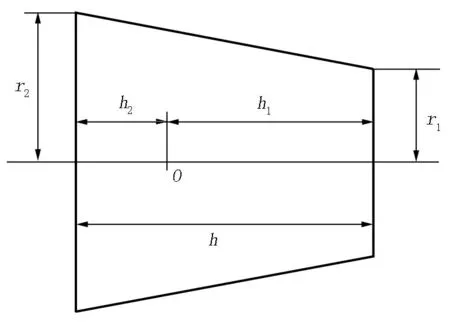
图1

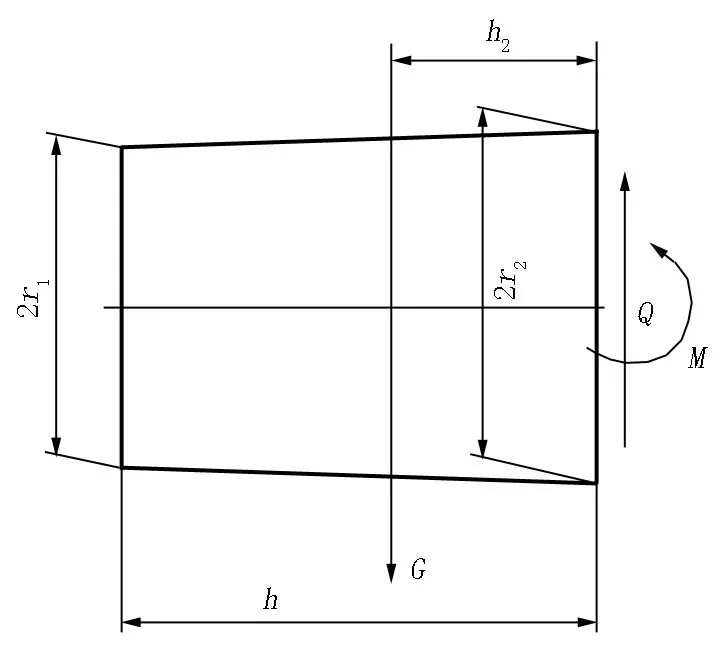
图2

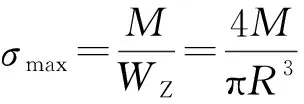
位置y的弯曲正应力：

(2)弯曲剪应力

最大弯曲剪应力：

位置y的弯曲剪应力：

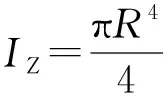
(3)两种强度考虑

弯曲强度条件：σmax≤σs=9.69 MPa，

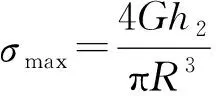
剪切强度条件：τmax≤τ(s)=5.59 MPa

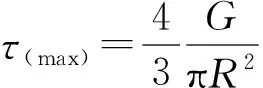
(4)Mises屈服准则

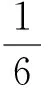
σx=σ，τxy=τ，σy=σz=τyz=τzx=0

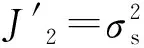
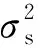
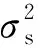
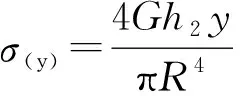
F(y)=σ(y)2+3τ(y)2

F(y)是一个开口朝上的抛物线，其最大值位于两端，即y=0，和y=R

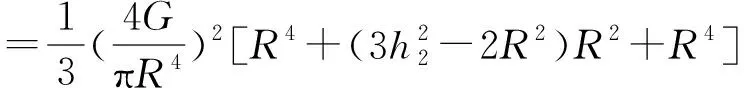
记录两种诊断方式的检查结果，并与最终手术治疗结果进行对比，统计两种方式的误诊、漏诊人数，以此计算各诊断方式的诊断准确率；记录两种诊断方式检查得出的突出征象，并与最终手术治疗结果进行对比，统计具体病因诊断的准确率。

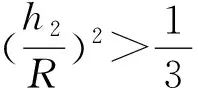
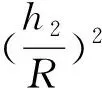
这个结果与前面的结论一致。为了有更大的保险系数，我们假设τs=σs/2，判断准则为：

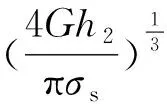
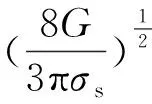
2 按照杠杆式假设推导公式

假设考虑钢锭钳口直径略小于套筒直径，则二者接触成为杠杆式，见图3。在A、B二处为线接触，B处平衡力矩为F1，这时支点A处承受的集中力为F，则有：

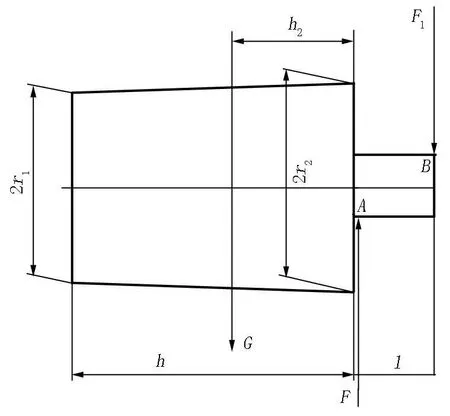
图3

应用剪应力强度理论，按此计算最小钳口直径R2：

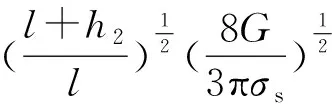
显然这个数值大于弯曲正应力强度理论计算出的数值。

这种杠杆式推导公式更接近于生产实际，且增大l有利于减小钳口直径R2的尺寸。

3 结论

(1)钳口与套筒紧密接触，弯曲正应力引起的抗拉破坏最大，钳口设计的最小直径应以此为准；

(2)钳口与套筒非紧密接触，钢锭钳口直径略小于套筒直径，剪切应力引起的破坏最大，钳口设计的最小直径应以此为准，同时可以考虑增大钳口长度可适当弥补钳口直径小的不足。

(3)套筒直径应以钳口与套筒非紧密接触方式的计算方法为准，非紧密接触更接近生产实际。