基于马尔可夫决策的P2P激励机制研究

王春枝 周 可 陈宏伟 陈 莉

（武汉理工大学计算机学院1） 武汉 430070） （湖北工业大学计算机学院2） 武汉 430068）

近年来，P2P网络因其所具有的开放性，自治性［1］等，但也因为它的这些特性使得在其应用中逐渐暴露出一系列的问题，安全问题尤为突出.马尔可夫预测法［2－3］它是一种只要知道现在的情况，就能确定未来状态，并不需要再对它过去的历史进行认识了解的预测方法.本文对P2P网络构建一个预测机制，对节点进行同步通告、监督，并对节点随机行为进行警示、约束、淘汰，促使对等网络中节点成功通信的概率增长，直至保持稳定.

1 马尔可夫预测法

1.1 Markov链

定义1 随机过程｛Xn，n＝0，1，2，…｝称为Markov链，若它只取有限个值，并且对于任意的n≥0，及任意状态i，j，i0，i1，…，in－1，有

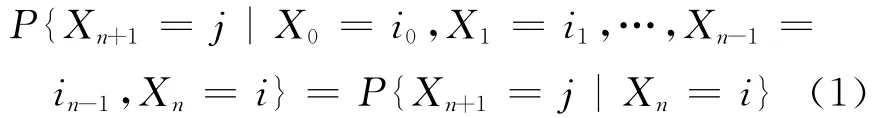
式中：Xn＝i为过程在时刻n处于状态i，称｛0，1，2，…｝为该过程的状态空间，记为E；P为系统从状态i经过一步转移到状态j的概率，其中Pij＝P｛Xn＋1＝j｜Xn＝i｝只与状态i，j有关.式（1）刻画了 Markov链的特性，即无后效性［4－5］.

1.2 转移概率

通过式（1），可以得知当系统从状态i通过一次转移到状态j的这一概率称为一步转移概率.通常，可以把一步转移概率拓展为矩阵的形式，令

由于概率是非负的，且随机过程必须转移到某一状态，可以看出pij（i，j∈I）有以下性质.

定义2 根据Markov随机过程，可根据一步转移概率矩阵，求出k步转移矩阵，称这一概率为Markov链的k步转移概率矩阵.

定义3 C－K方程［6］，对一切c，d≥0，i，j∈I有：

1.3 稳态分布

定义4 若 Markov链｛En：n≥0｝的状态空间I为有限集，且其转移概率矩阵Pij满足Pij＞0，∀i，j∈I，则存在I上惟一的概率分布D＝（D1，D2，D3，…，Dn），使 得 对 所 有i，j∈I 及min（Pij：ij∈I）≤1／n，都有：（1）D＝DP；（2）Pn＝.

2 基于Markov的预测机制

2.1 节点状态分类

根据节点在网络中合作概率大小，以及合作态度将其状态分别为4类：（1）积极合作（E1）是网络中合作概率最优的节点状态，该类状态节点会积极地将其资源传送给其他节点，很少出现背叛，或是失误，但若网络大部分节点出现群体侥幸心理时，该类状态不排除有转移的可能性；（2）常规合作（E2）是网络中合作概率较良好的状态，该类状态的节点有选择性的将资源传给需要它的节点，当节点碰到其交互对象所需的资源不是它所拥有的，将拒绝与其通信.处于这一群体的节点，往往为求得最大收益，向其他状态转移的概率较大；（3）消极合作（E3）是网络中合作概率相对一般或是较低的状态，该状态节点在网络中一直从其他节点搜索，下载资源，起初未对网络进行资源贡献，直至系统机制对网络中自私节点进行警告时，这一态度的节点会为防止下一次被机制淘汰，而被迫进行资源共享.这一类型状态与常规状态一样，由于自私性原因，是最易向其他状态转移的状态；（4）自私（E4）是网络中合作概率最低的状态，这一态度的节点，在网络中一直从其他节点索取资源，从不对网络进行资源贡献.但也有极少数这类状态的节点会因网络机制的约束，被迫向其他状态转移.

根据网络中节点合作行为的选择概率分布，对节点的这四类状态进行概率区间划分，设定节点状态概率区间为

例如，t时刻，根据本文设定的节点状态概率区间，自私状态P1∈（0，x1］，消极状态 P∈（x1，x1＋x2］，常规状态P3∈（x1＋x2，x1＋x2＋x3］，积极状态P4∈（x1＋x2＋x3，x1＋x2＋x3＋x4］.

2.2 预测机制规则

本文通过博弈论经典的囚徒困境模型对网络中节点进行心理分析.可将这一节点交互的过程看成是一种博弈，从表1中，能很明显地看出，节点往往表现出更多的理性，它会为了使得自身利益最大化，而选择去欺骗，只要网络未对节点群体采取约束管理措施，节点很容易产生侥幸心理，从而一直去选择欺骗其他节点，这也是产生P2P网络安全问题的原因所在.

表1 囚徒困境模型

2.2.1 预测机制设置 根据这一博弈中节点行为选择心理，以及针对网络中节点的4种状态，在P2P网络中设置一种预测系统机制，并将机制对节点的行为约束规则统计如下.

1）对于进入对等网络的各状态节点，机制允许初始状态为自私的节点存在.

2）每间隔t（t＞0）时刻，机制对当前节点状态分布进行统计，并运用马尔可夫链对网络节点未来状态进行预测.

3）每隔t时刻后，机制根据统计的数据对节点进行通告，并根据预测的节点状态转移矩阵，针对节点的每种状态采取对应的措施，相应措施如下：（1）对于积极状态，机制不会对其采取约束措施；（2）对于常规状态，以博弈收益矩阵为前提，当该类状态节点对其交互对象采取背叛行为，得到更大的收益时，为防止其一直保持侥幸心理，机制将在每隔t时间后对该类状态进行观测，若该状态以转移向消极，更或是自私，机制将会对其进行约束，甚至淘汰；（3）对于消极状态，为防止该状态节点一直保持不贡献的状态，机制会在t时刻后对该类节点进行激励，若节点有积极趋势，则将其保留，若继续消极，则将其淘汰；（4）对于自私状态，根据这一状态的特性，每隔t时刻机制直接将这类节点淘汰出网络.

4）经过机制多次反复约束，若在某时刻节点状态处于较为积极的趋势，机制为保持网络的稳定性，将不再对网络进行预测，而是直接维护，淘汰自私节点，保留其余节点.

2.2.2 预测机制的运行 通过对网络节点状态统计，本文总结四种节点状态的转换趋势，见图1.

图1 网络整体节点状态转移图

图1 显示，每种状态只能由自身或向相邻的状态进行转移，不能进行跨越转移，例如积极状态不能直接转移到自私状态.这一状态转移趋势遵循节点在网络中行为规律，若节点抱有侥幸心理，通过逐渐背叛，合作概率逐渐减少，进而由积极→常规→消极→自私［6］.

基于马尔可夫链的预测方法，机制会对每隔t时刻的节点状态进行统计，设在t时刻，网络中四类节点状态为E，E∈（En，n＝1，2，3，4），节点状态的初始分布为 Pt（0）＝（Pt1（0），Pt2（0），Pt3（0），Pt4（0））.根据图1节点的状态转移情况，构建一个节点状态概率转移矩阵.假设处于Ei状态的节点个数为mi，由Ei转移到状态Ej的个数为mij，则可以得到网络中节点由Ei转移到状态Ej的状态转移概率Pij，且Pij＝mij／mi.由此可得，网络节点的4种状态转移矩阵P

预测机制根据这一节点状态转移矩阵，可以得到未来任意时刻网络节点状态的转移情况，即，假设在n时刻，网络节点状态转移矩阵P［n］＝P（0）·Pn，并由D＝D·P，得到网络节点状态的稳态分布向量，进而得到未来网络节点状态的稳态转移概率矩阵.

3 仿真分析

在Ti时刻，统计前t段时间内的节点状态分布数据，得到表2.

表2 t时间段内节点状态转移分布

根据表2数据统计，可建立节点状态转移矩阵P为

式（7）中，在未加入系统机制的情况下，积极状态与自私状态大部分是向自身转移，只有极少数向其他状态转移，而在大多数节点存在的常规状态和消极状态逐步两极分化，并更多地转移向自私状态，由于节点进行博弈行为选择过后发现自私获取资源远远比贡献资源要轻松的多，于是更多地采取背叛行为，形成侥幸心理，导致网络资源利用不均，节点诚信问题的严重.

由Ti时刻网络的4种节点状态分布，以及其状态转移概率矩阵，可计算得到未来节点状态的稳态分布向量D＝［0.080 0 0.051 0 0.140 2

0.728 8］.分析这一稳态向量，可预测到若网络节点状态继续由这一概率矩阵进行转移，网络总体状态必然趋向于自私，也就是由于节点侥幸心理群体化，改变节点博弈行为选择，最终影响网络的稳定性.

由于提前预知到网络节点博弈行为的这一恶化，节点状态未来的改变趋势，本文在这一时刻对网络中设置预测机制，从细节入手，对节点博弈行为选择进行约束，从而对节点4种状态转移进行控制，并实时对网络节点状态进行统计，淘汰顽固自私节点.

本文利用matlab仿真软件，对预测机制未加入前的网络节点状态分布进行仿真，并对得到预测机制约束后的网络节点状态进行了仿真对比，得到以下曲线图.

通过图2和图3可看到，只要机制对节点进行一定的行为约束，节点的状态趋势有稍微的转变，整个网络的节点状态在未来的发展趋势都会有很大的变化，证实了预测机制的存在对于P2P网络是有积极作用的，其对于网络的稳定性，和节点间的信任都有了很大的辅助作用.也可以看到节点状态的任意变化都会对整个网络造成很大的影响，所以机制的存在是有必要的，而且需要预测机制同时在每时刻都对网络节点状态进行跟踪、预测，以防止网络出现瘫痪的可能.

图2 未加入预测机制后的网络节点状态分布

图3 加入预测机制后的网络节点状态分布

4 结束语

本文通过对网络节点历史行为进行统计，根据节点选择合作行为概率将节点状态进行分类，并对节点这4种状态进行分析，研究节点行为选择趋势.进而在P2P网络中设置一种预测机制，通过对节点状态分布进行统计，对未来网络节点状态发展趋势进行预测，通过预测结果及时选择相应地策略对网络节点进行约束.通过仿真，证实了该机制对网络节点自私行为具有约束性，有效性，进而能够维护网络的稳定性.今后将继续对马尔可夫随机过程与P2P信任博弈模型的结合进行更为细致的研究.

［1］Yu Yijiao，Jin Hai.A survey on overcoming free riding in peer－to－peer networks［J］.Chinese Journal of Computers，2008，3l（1）：1－15.

［2］Cao X R.Semi－markov decision problems and performance sensitivity analysis［J］.IEEE Trans on Automatic Control，2003，48（5）：758－769.

［3］BumPkin C，Agrawa1D.A game theoretic framework for incentives in P2Psystems［C］／／Proc.of the third International Conference on Peer－to－peer Computing，2003.

［4］Wang Y ，Vassileva J.Bayesian network based trust model［C］／／Proceedings of the IEEE／WIC International Conference on Web Intelligence（WI＇03），Halifax，Canada，2003：372－378.

［5］RabinerL R.A tutorial on hidden Markov models and selected applications in speech recognition［J］.Proceedings of the IEEE，1989，77（2）：257－286.

［6］Park H S，Lee S W.A truly 2－D hidden markov model for off－line handwritten character recognition［J］.Pattern Recognition，1998，31（2）：1 864－1 894.